Show that the angle made by the string with the vertical in a conical

Topper's Solved these Questions

BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18videos
CIRCULAR MOTION
BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5videos
CIRCULAR MOTION
BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective
14videos
CIRCULAR MOTION
BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27videos
COMMUNICATION SYSTEM

Knowledge Check

Question 1 - Select One
A non-uniform bar of weight $W$ and weight $L$ is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are $θ_{1}$ and $θ_{2}$ respectively.
The distance $d$ of the centre of gravity of the bar from left end is.
.
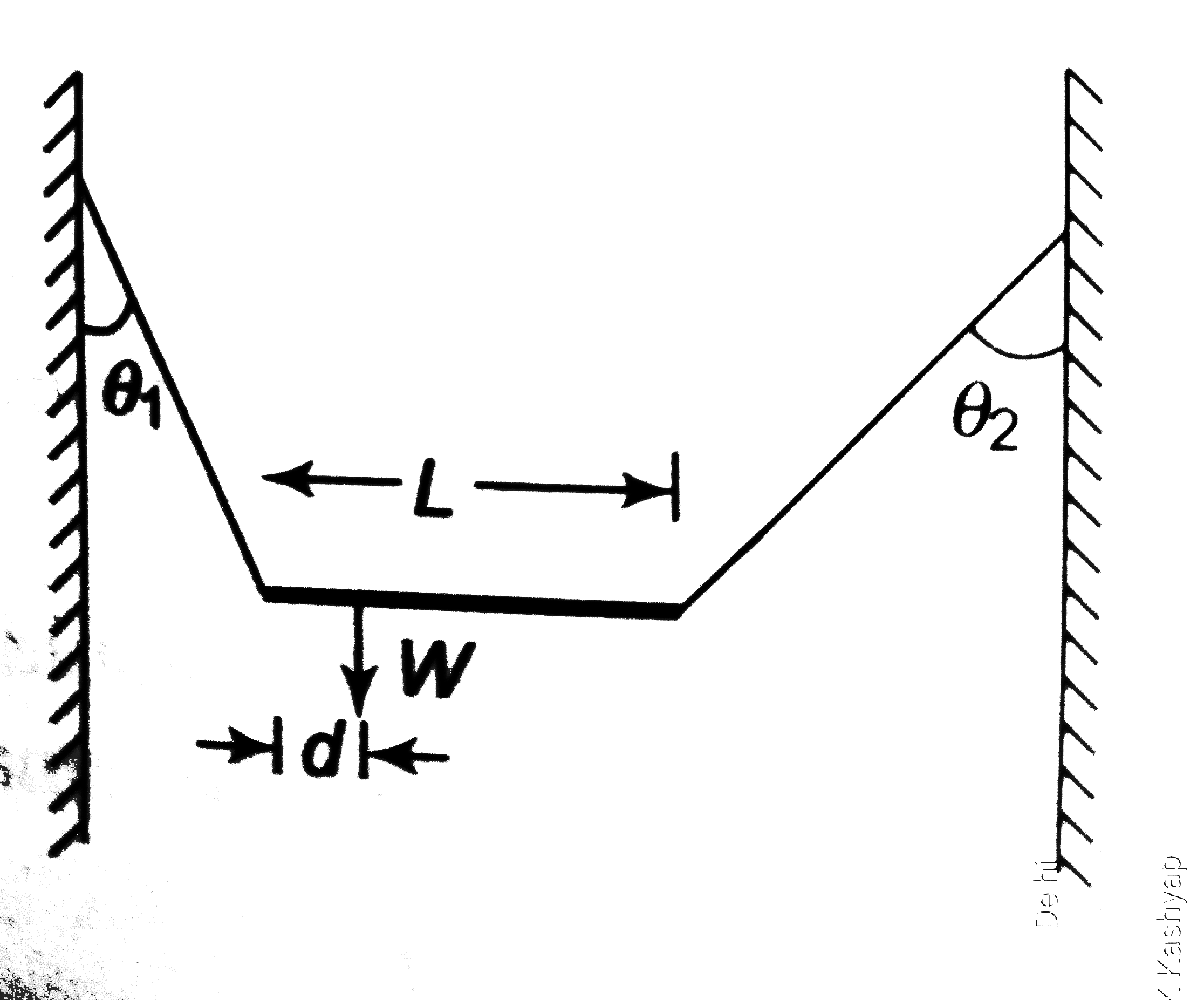A $L (\frac{{tan θ}_{1} + {tan θ}_{2}}{{tan θ}_{1}})$
B $L (\frac{{tan θ}_{1}}{{tan θ}_{1} + {tan θ}_{2}})$
C $L (\frac{{tan θ}_{2}}{{tan θ}_{1} + {tan θ}_{2}})$
D $L (\frac{{tan θ}_{1} + {tan θ}_{2}}{{tan θ}_{2}})$
Question 2 - Select One
A particle of mass $m$ is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity $u = \sqrt{\frac{5}{2} g l}$

The maximum angle made by the string with downward vertical is
A ${cos}^{- 1} (\frac{1}{4})$
B ${sin}^{- 1} (\frac{1}{4})$
C $\frac{π}{2} + {cos}^{- 1} (\frac{1}{4})$
D $π - {cos}^{- 1} (\frac{1}{4})$
Question 3 - Select One
Two identical particle are attached at the ends of a light string which passes through a hole at the centre of a table another particle on the table is made to revolve with angular velocity $ω_{1}$ . One of the particles is made to move in a horizontal circle as a conical pendulum with angular velocity $ω_{2}$ . If $l_{1}$ and $l_{2}$ are the length of the string over and under the table , then in order that particle under the table neither moves down nor moves up the ratio $\frac{l_{1}}{l_{2}}$ is :

A $\frac{ω_{1}}{ω_{2}}$
B $\frac{ω_{2}}{ω_{1}}$
C $\frac{ω_{1}^{2}}{ω_{2}^{2}}$
D $\frac{ω_{2}^{2}}{ω_{1}^{2}}$

Show that the angle made by the string with the vertical in a conical pendulum is given by $cos θ = \frac{g}{L ω^{2}}$ , where $L$ is the string and $ω$ is the angular speed.

The correct Answer is:A

$R = L sin θ$

$T sin θ = m R ω^{2} = m (L sin θ) ω^{2}$
:. $T = m L ω^{2}$
Now, $T cos θ = m g$
:. $cos θ = \frac{m g}{T} = \frac{m g}{m L ω^{2}} = \frac{g}{L ω^{2}}$

Topper's Solved these Questions

Similar Questions

Knowledge Check

A non-uniform bar of weight $W$ and weight $L$ is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are $θ_{1}$ and $θ_{2}$ respectively.
The distance $d$ of the centre of gravity of the bar from left end is.
.

A particle of mass $m$ is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity $u = \sqrt{\frac{5}{2} g l}$

The maximum angle made by the string with downward vertical is

DC PANDEY-CIRCULAR MOTION-Level 1 Subjective

Show that the angle made by the string with the vertical in a conical pendulum is given by cosθ=gLω2 , where L is the string and ω is the angular speed.

The correct Answer is:A

R=Lsinθ Tsinθ=mRω2=m(Lsinθ)ω2 :. T=mLω2 Now, Tcosθ=mg :. cosθ=mgT=mgmLω2=gLω2

Topper's Solved these Questions

Similar Questions

Knowledge Check

A non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from left end is. .

A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl The maximum angle made by the string with downward vertical is

DC PANDEY-CIRCULAR MOTION-Level 1 Subjective

Show that the angle made by the string with the vertical in a conical pendulum is given by $cos θ = \frac{g}{L ω^{2}}$ , where $L$ is the string and $ω$ is the angular speed.

$R = L sin θ$

$T sin θ = m R ω^{2} = m (L sin θ) ω^{2}$
:. $T = m L ω^{2}$
Now, $T cos θ = m g$
:. $cos θ = \frac{m g}{T} = \frac{m g}{m L ω^{2}} = \frac{g}{L ω^{2}}$

A non-uniform bar of weight $W$ and weight $L$ is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are $θ_{1}$ and $θ_{2}$ respectively.
The distance $d$ of the centre of gravity of the bar from left end is.
.

A particle of mass $m$ is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity $u = \sqrt{\frac{5}{2} g l}$

The maximum angle made by the string with downward vertical is