Find the minimum value of F and the tension in the string so that the blocks move with constant velocity. The coefficient of friction at all surfaces is μ.
(a)
(b) 
( c ) 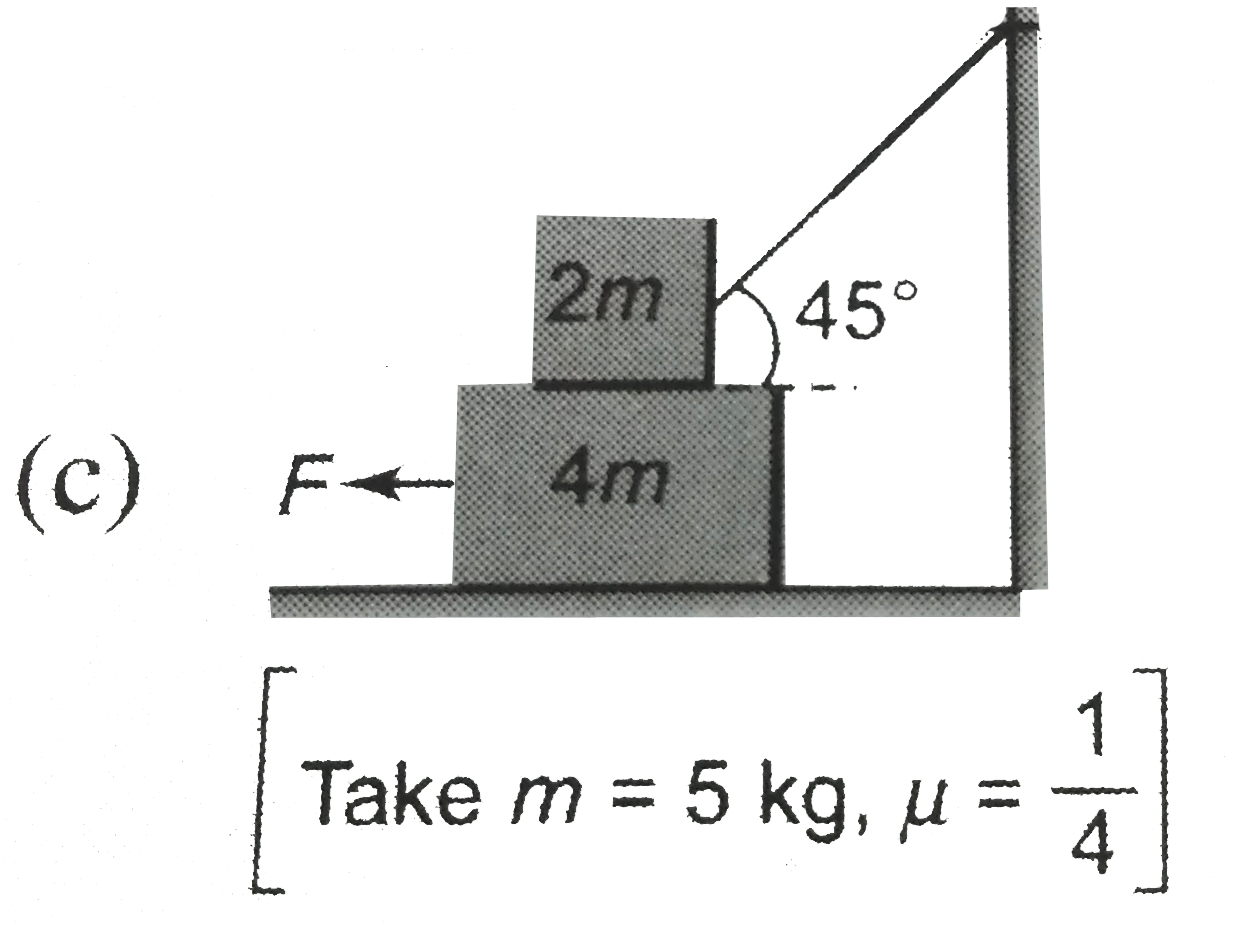
(d)
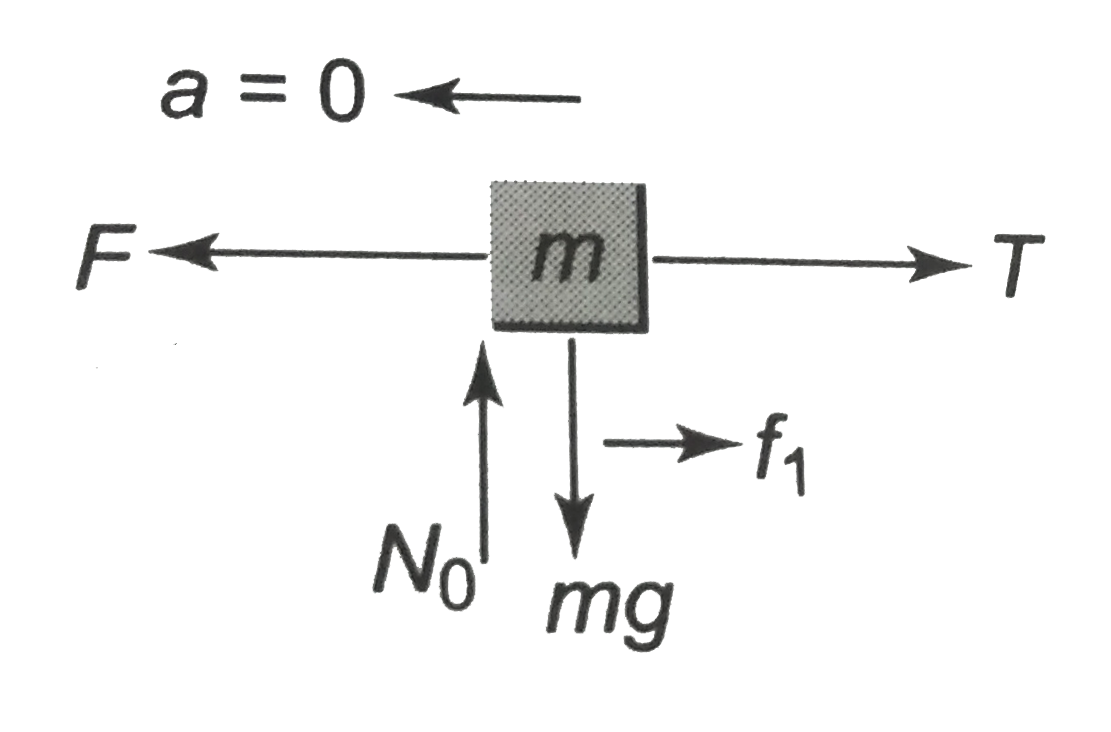
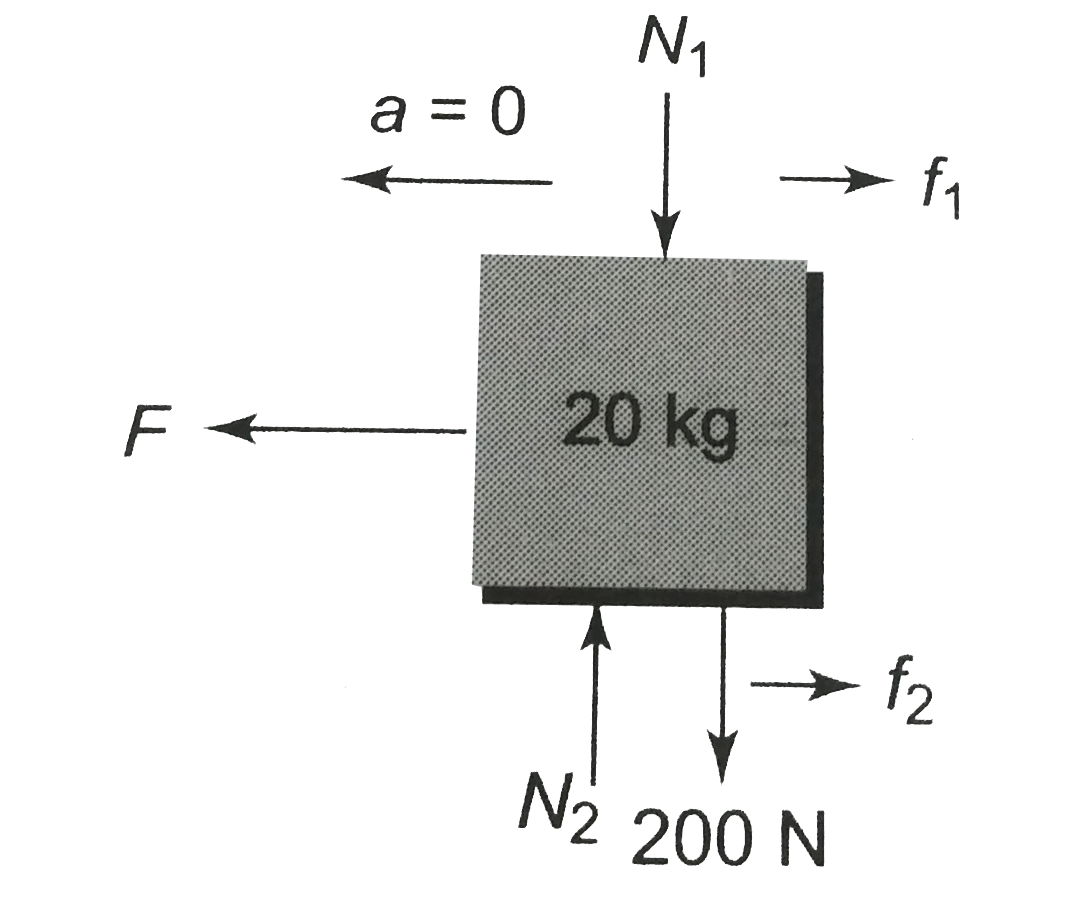
(a) N0=mg,f1=μN0=μmg
F−T−f1=0 (i)
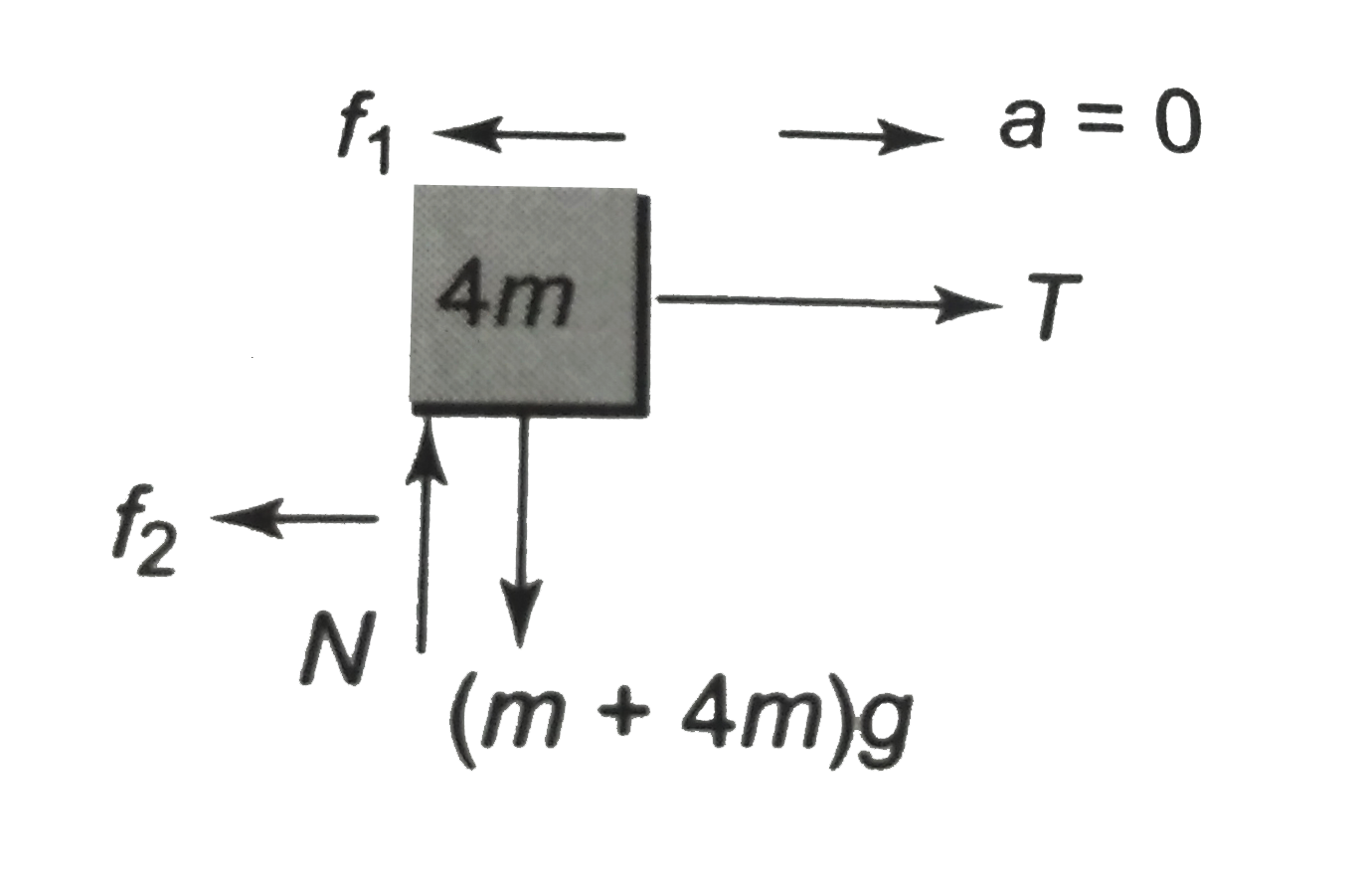
N=(m+4m)g=5mg,f2=μN=5μmg
T−f1−f2=0 (ii)
T=f1+f2=6μmg
F=T+f1=7μmg
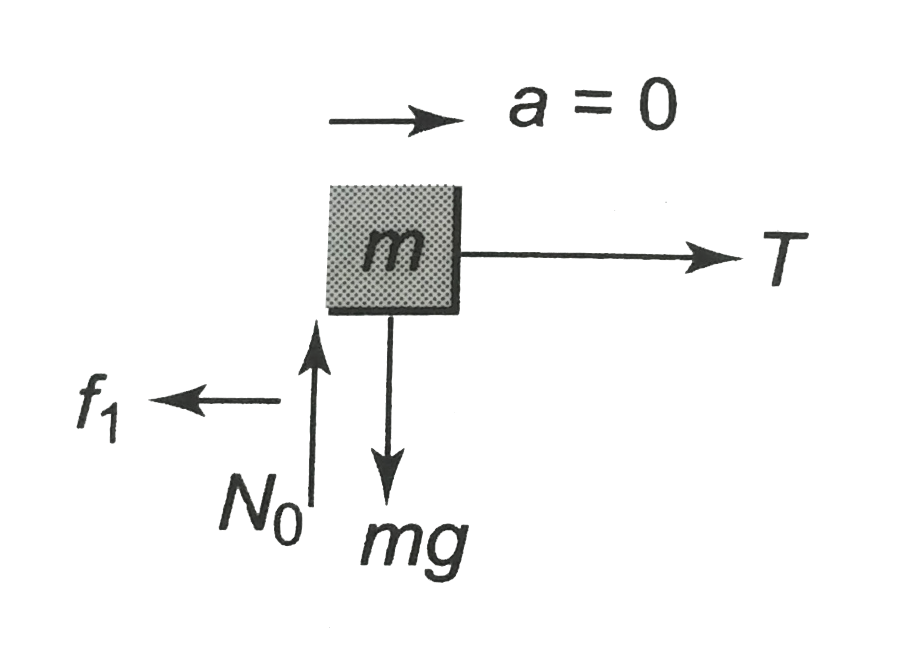
(b) N0=mg,f1=μN0=μmg
T−f1=0⇒T=μmg
N=(m+4m)g=5mg,f2=μN=5μmg
F−T−f1−f2=0
F=T+f1+f2=7μmg
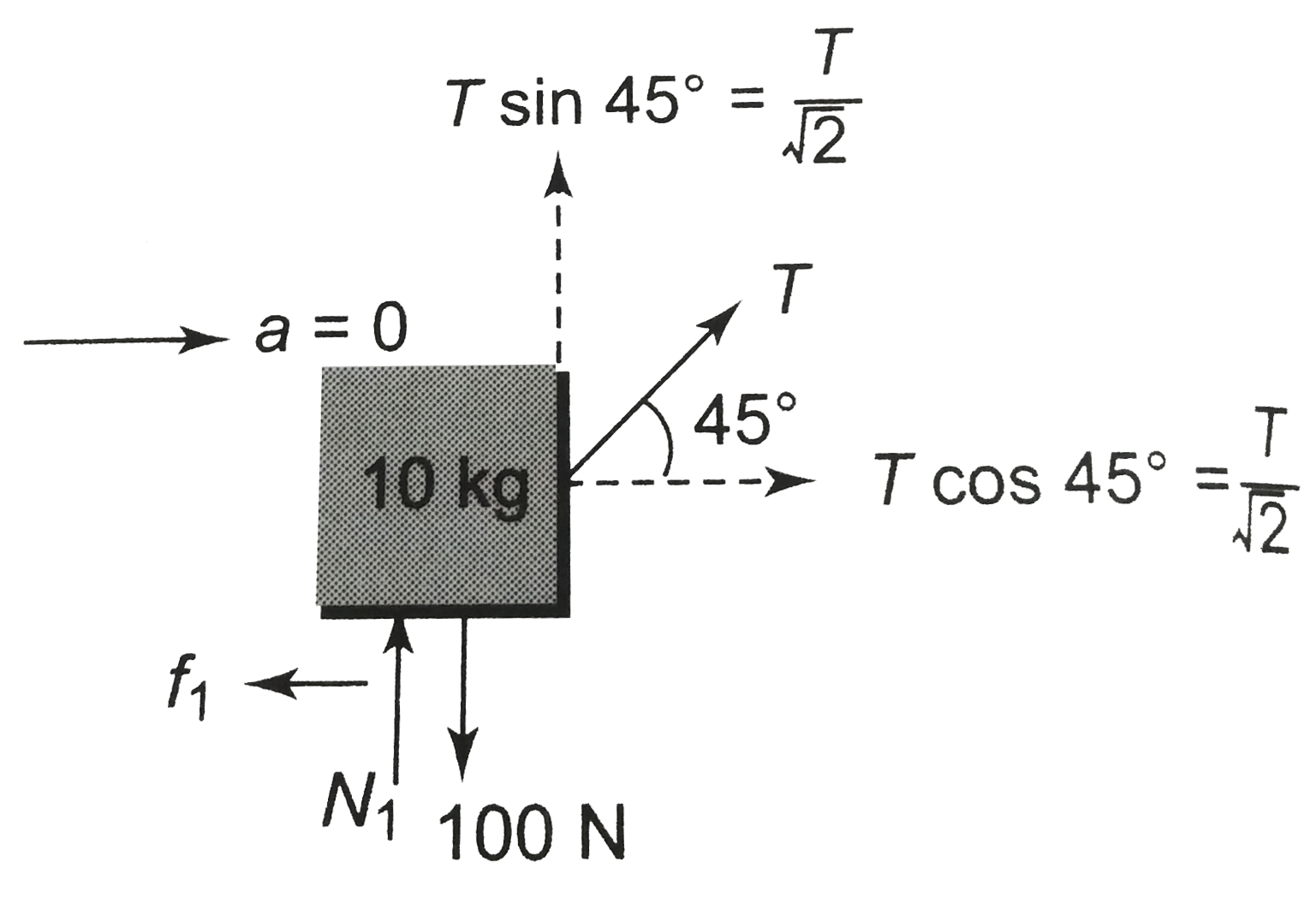
(c ) ↑⏐
⏐
⏐⏐:N1+T√2−100=0⇒N1=100−T√2
f1=μN1=14(100−T√2)=25−T4√2
→:T√2−f1=0⇒T√2−25+T4√2⇒5T4√2=25
T=20√2N
N1=100−T√2=80N,f1=25−T4√2=20N
↑:N2−N1−200=0⇒N2=N1+200=280N
f2=μN2=14×280=70N
←:F−f1−f2=0⇒F−20−70=0
F=90N
Applied force F=90N , Tension T=20√2N
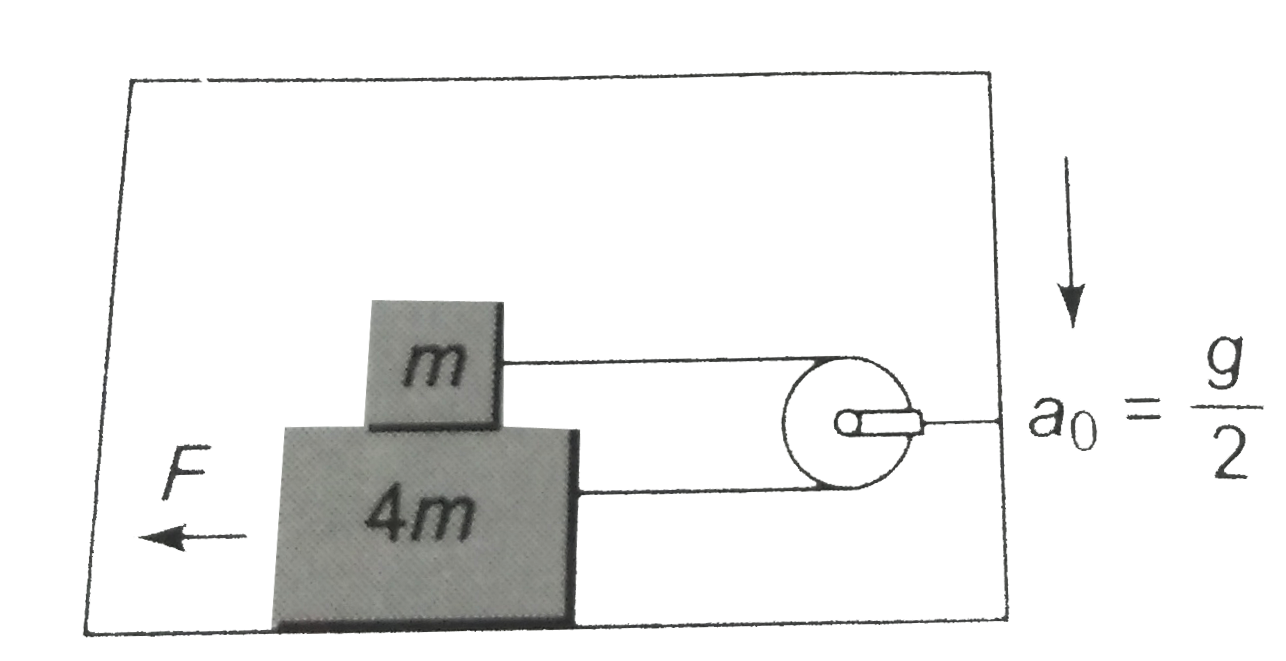
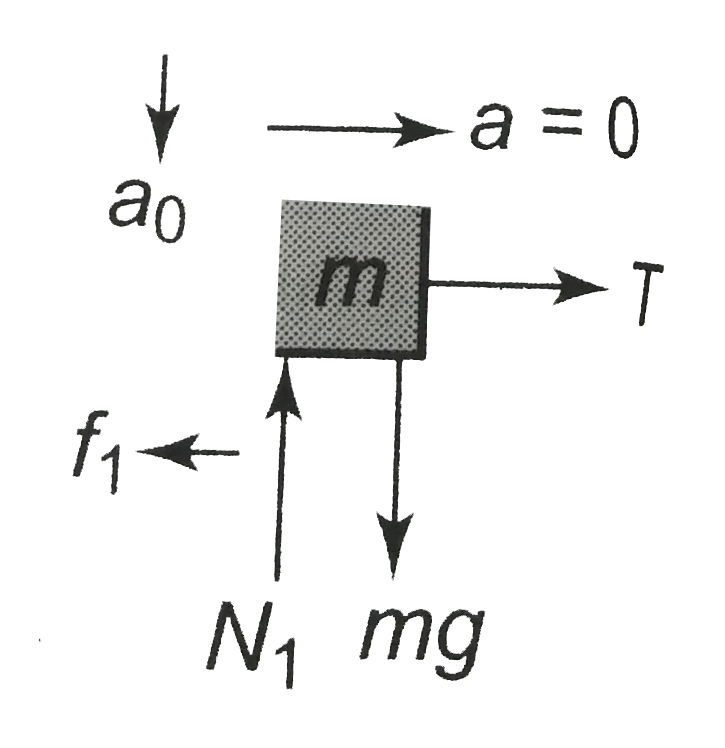
(d) m:↓,mg−N1=ma0
N1=m(g−a0)=mg2
f1=μN1=μmg2
→:T−f1=0⇒T=f1=μmg2
4m:⏐⏐
⏐↓:4mg+N1−N2=4ma0=4mg2
N2=2mg+mg2=5μmg2
←:F−T−f1−f2=0
F=T+f1+f2=7μmg2 ltbr5gt Note : When a block is moving in a lift with acceleration a0(a0<g) in downward direction , we can use (g−a0) in place of g. In part (b) , for calculating normal reactions N1 and N2 , replace gby(g−a0).


Topper's Solved these Questions
Similar Questions
Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
 View Solution
View Solution
Three blocks are connected as shown in the figure. Valculate the minimum force required to move the body with constant velocity. The coefficient of friction at all surfaces is 0.25.View Solution
Knowledge Check
- Question 1 - Select One
A homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
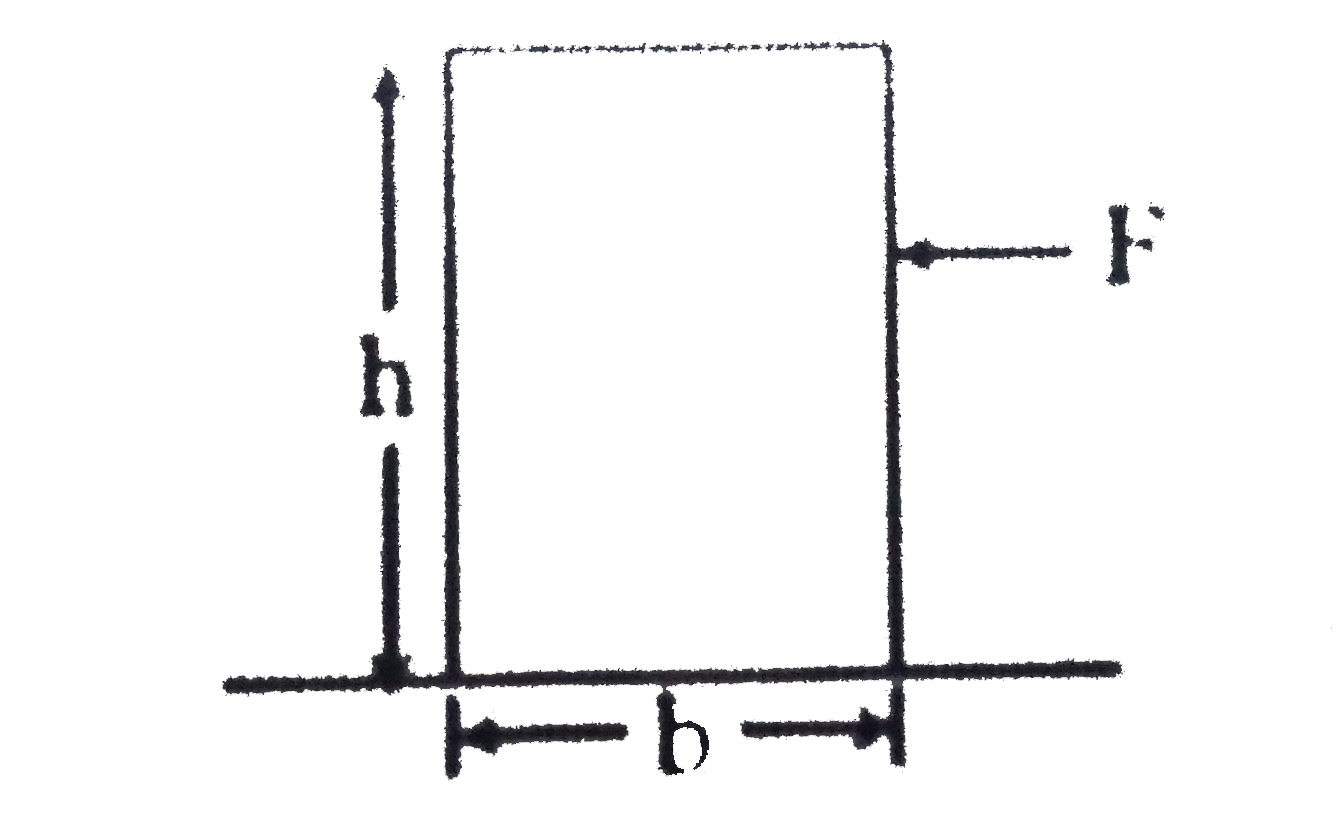 Ab2μB2bμCbμD2√2bμ
Ab2μB2bμCbμD2√2bμ - Question 2 - Select One
The minimum acceleration that must be impprted to the cart in the figure so that the block A will not fall (given μ is the coefficient if friction between the surface of block and cart) is given by:
 AμgBg/μCg√μDμg
AμgBg/μCg√μDμg - Question 3 - Select One

Find the minimum value of F for which 5 kg being to slide if the coefficient of friction between the blocks is changed to 0.5 :A10 NB30 NC45 NDno value exist
Find value of pulling force F for which block just moves. Given coefficient of friction for surface is μ.
 View Solution
View SolutionThe block shown is moving with constant velocity. Find μk between the block and the surface.
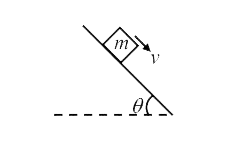 View Solution
View SolutionIf force F is gradually increased from zero to 50N , tehn (a) find the minimum contact force, (b) find the maximum value of angle of friction when F=30N , (d) find the angle of friction when the block is moving with constant velocity and ( e) sketch a graph between friction and applied force.
 View Solution
View SolutionA horizontal force Facts on the lower block which is connected with another block kept on it. The two blocks are connected by a light, smooth inextensible string that passes over a fixed pulley. If the co-efficient of friction between all contact surfaces is u , then minimum value of F so that the block starts moving.
View SolutionIn the system shown in fig., block A and C are placed on smooth floors and both have mass equal to m1. Blocks B and D are identical having mass m2 each. Coefficient of friction
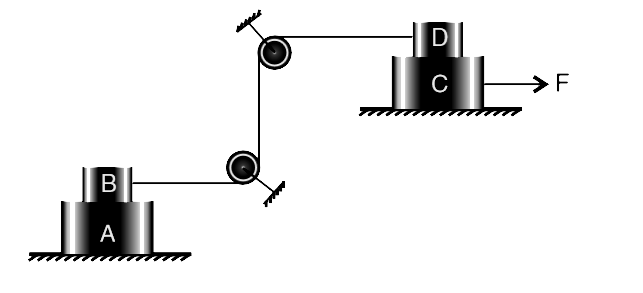
Between A and B and that between C and D are both equal to μ. String and pulleys are light. A horizontal force F is applied on block C and is gradually increased.
(a) Find the maximum value of F (call it F0) so that all the four blocks move with same acceleration.
(b) Will the value of F0 increase or decrease if another block (E) of mass m2 is placed above block D and coefficient of friction between E and D is μ?View Solution

