Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

The correct Answer is:F=mgμ
Step by step video & image solution for Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is mu. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (WORK POWER & ENERGY)
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (CIRCULAR MOTION)
Explore 16 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (NEWTONS LAWS OF MOTION)
Explore 44 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
Find the magnitude of the horizontal force F required to keep the block of mass m stationary on the smooth inclined plane as shown in the figure.

View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
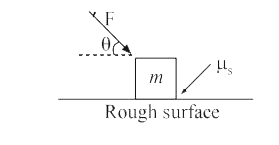
View Solution
Knowledge Check
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of theseA homogenous block of mass m, width b and height h is resting on a rough horizontal surface A horizontal force F is applied to it , which makes it to move with a constant velocity . The coefficient of friction between block and surface is μ Find the greatest height at which force F may be applied to slide the block with out tipping over
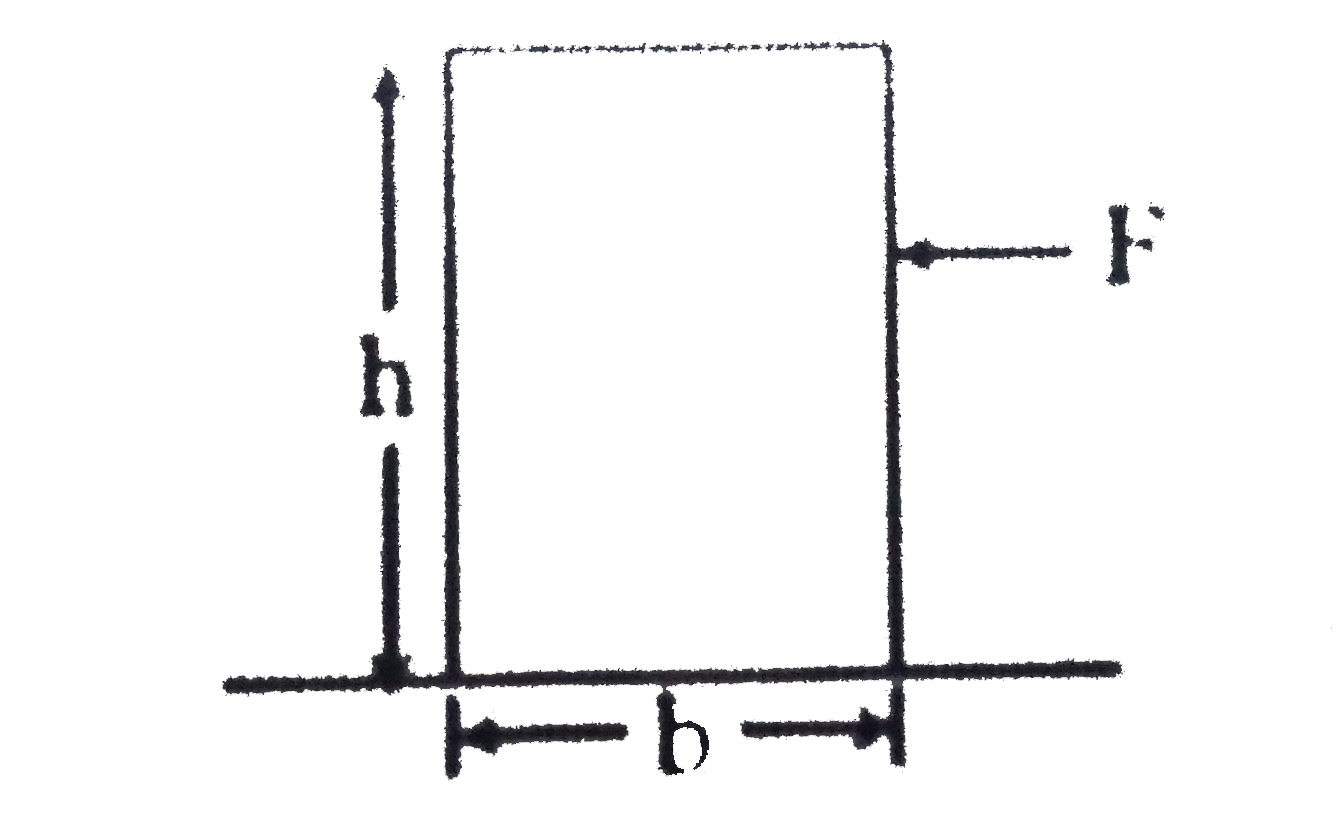 Ab2μB2bμCbμD2√2bμ
Ab2μB2bμCbμD2√2bμIn the given situation, what is the minimum mass of block A so that block B remains stationary with respect to the wall? The coefficient of friction is μ between wall and block. All other surfaces are smooth.
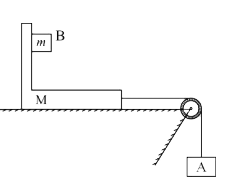 A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1
A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1
Find the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionA block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top is it. An increasing horizontal force F=αt is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is μ1 coefficient of friction between the blocks is μ1 and that between the lower block and the table is μ2, then what is the maximum possible value of μ1/μ2 ?
View SolutionIn the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
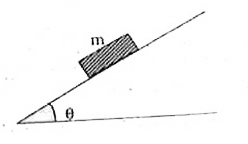
View SolutionA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution