Find the moment of Inertia of a cuboid along the axis as shown in the figure.
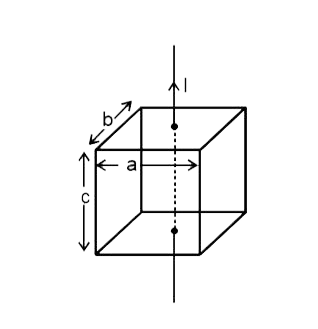
After compressing the cuboid parallel to the axis I
=M(a2+b2)12
Topper's Solved these Questions
Similar Questions
Knowledge Check
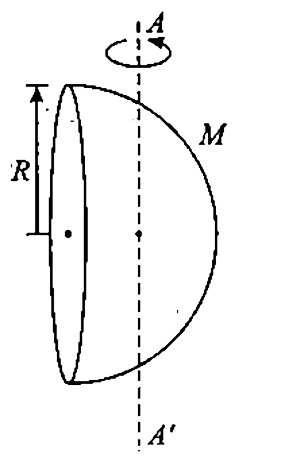
Find the moment of inertia of a hemisphere of mass M and radius R shown in the figure, about an axis AA' tangential to the hemisphere.
 AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2
AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2The moment of inertia of a thin square plate ABCD, as shown A in the figure, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of
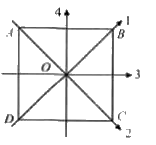 Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4 ltbRgt where l1,l2,l3 and l4 are respectively the moments of inertia about axis 1, 2, 3 and 4 which are in the plane of the plate.
Al1+l2Bl3+l4Cl1+l3Dl1+l2+l3+l4 ltbRgt where l1,l2,l3 and l4 are respectively the moments of inertia about axis 1, 2, 3 and 4 which are in the plane of the plate.The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
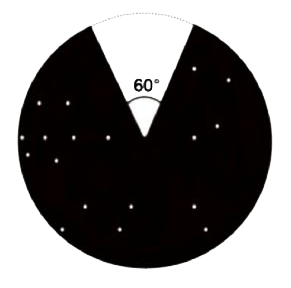 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212
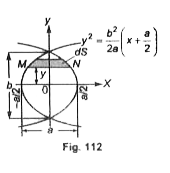
Find the moment of inertia about the x-axis of the figure bounded by two parabolas with dimensions indicated in.
View SolutionA uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

View SolutionFind the moment of inertia of a disk about an axis passing through a point on its circumference perpendicular to its plane.
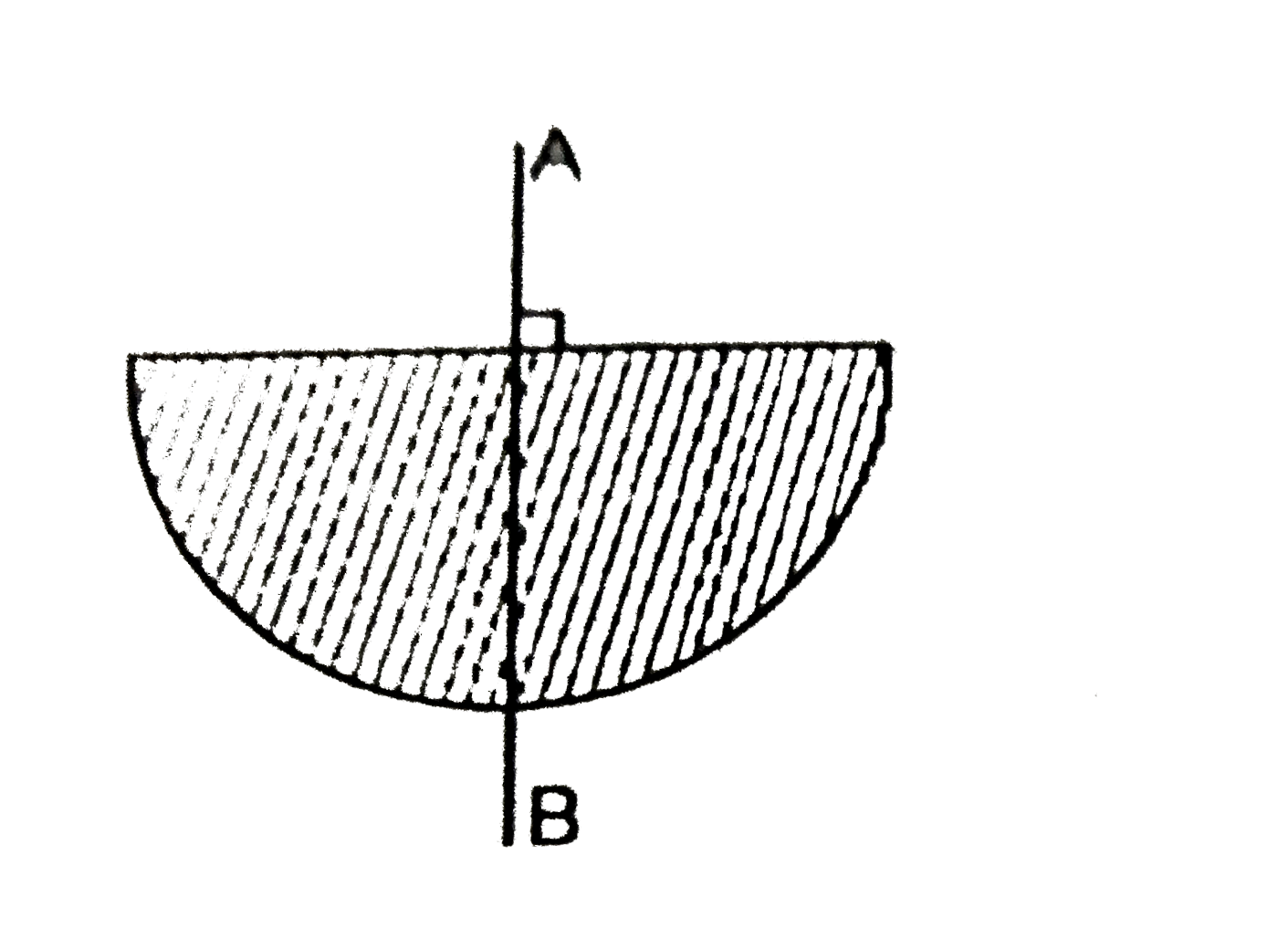
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
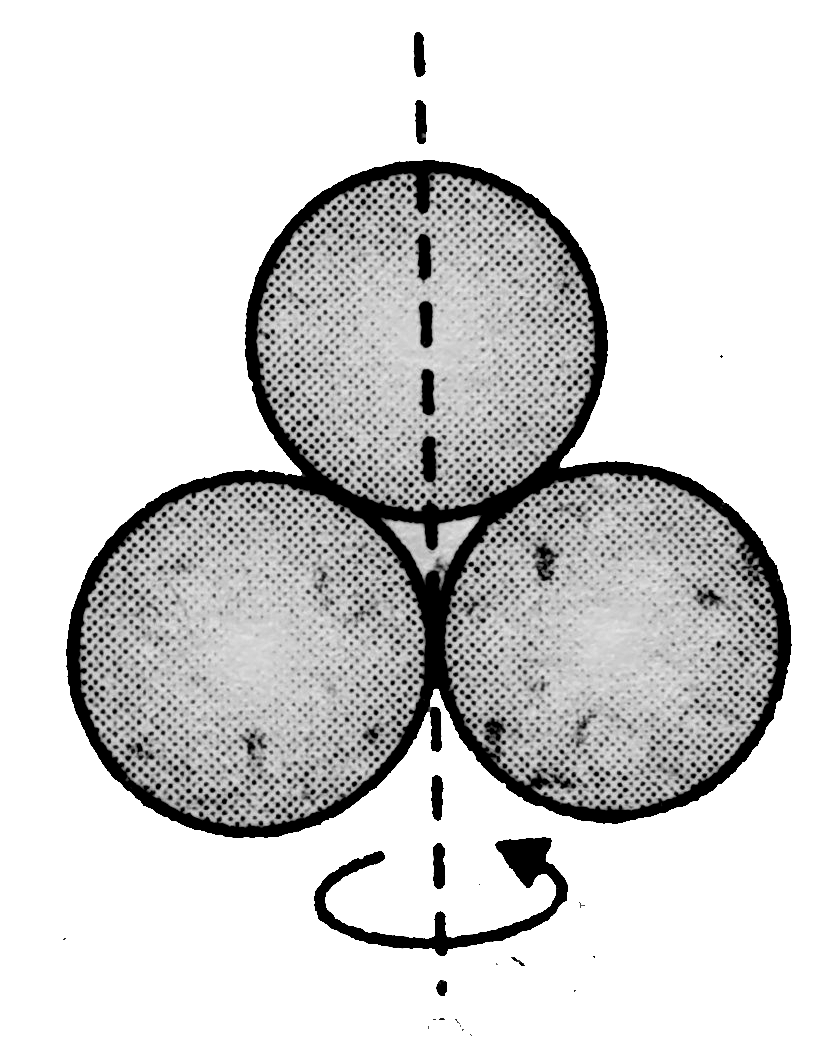
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View Solution