A uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

For simplicity let us use a mathematical trick. We consider the portion of the given disc as the superposition of two complete discs (whithout holes), one of positive density and radius R and other of negative density but of same magnitude and radius R/2.
As (area) α (mass), the respective masses of the considered discs are (4m/3) and (−m/3) respectively, and these masses can be imagined to be situated at their respective centres (C.M). Let us take point O as origin and point x-axis towards right. Obviously the C.M. of the shaded position of given shape lies on the x-axis. Hence the C.M. (C) of the shaded portion is given by
xc=(−m/3)(−R/2)+(4m/3)0(−m/3)+4m/3=R6
Thus C.M. of the shape is at a distance R/6 from point O toward x-axis.
Using parallel axis theorem bearing in mind that the moment of inertia of a complete homogeneous disc of radius m0 and radius r0 equals 12m0r20. The moment of inertia of the small disc of mass (−m/3) and radius R/2 about the axis passing through point C and perpendicular to the plane of the disc
I2C=12(−m3)(R2)2+(−m3)(R2+R6)2
=−mR224−427mR2
Similarly I1C=12(4m3)R2+(4m3)(R6)2
=23mR2+mR227
Thus the sought moment of inertia,
IC=I1C+I2C=1524mR2−327mR2=3772mR2

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
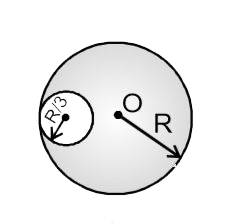 View Solution
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correct - Question 2 - Select One
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2 - Question 3 - Select One
A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
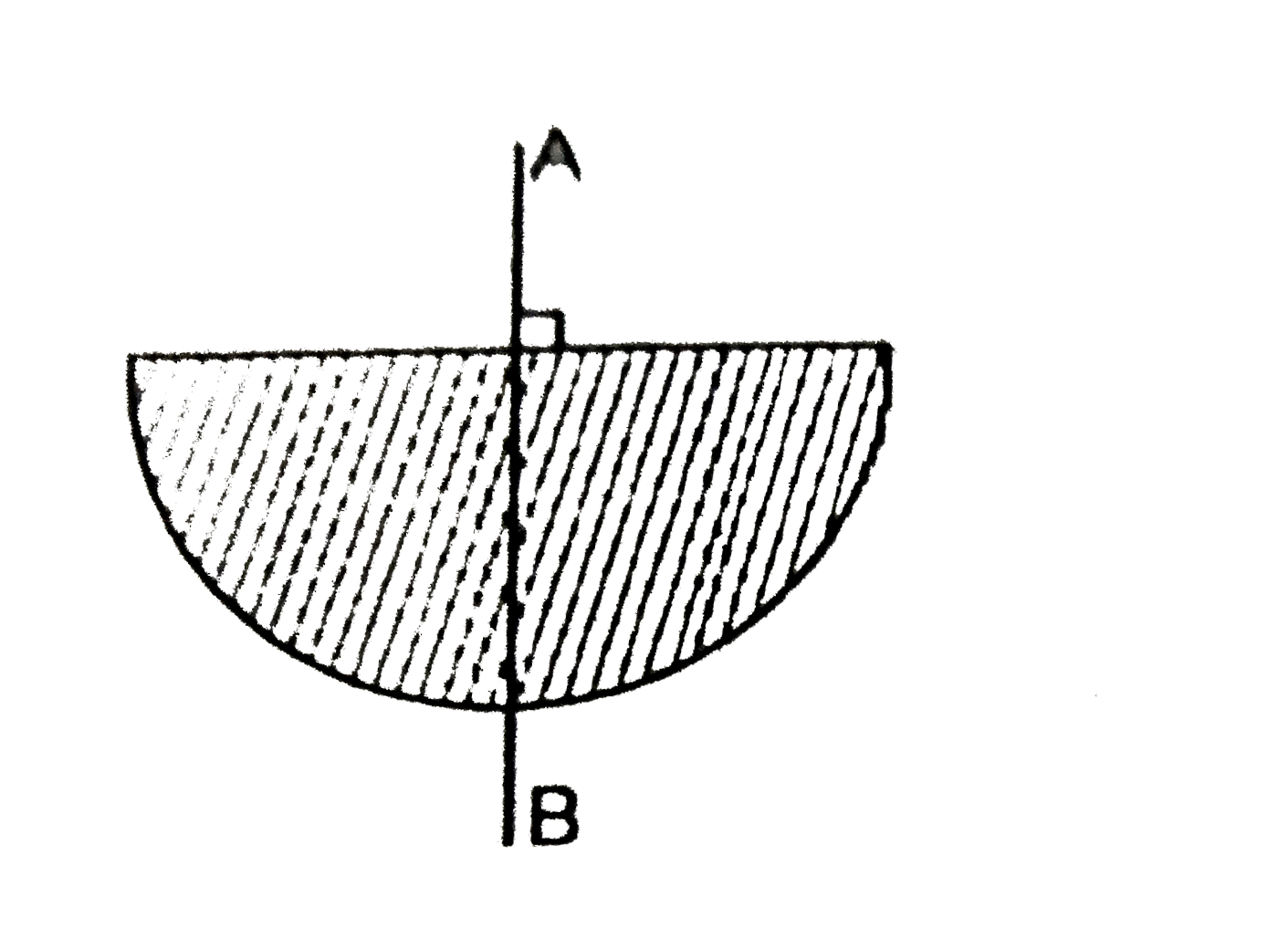 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
 View Solution
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 View Solution
View SolutionThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
View Solution

