Find the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and (a) in the plane of the ring (b). perpendicular to the plane of the ring.
Video Solution
Text Solution
Moment of inertia of a circular ring of mass M and radius R about the diameter AB, Fig.
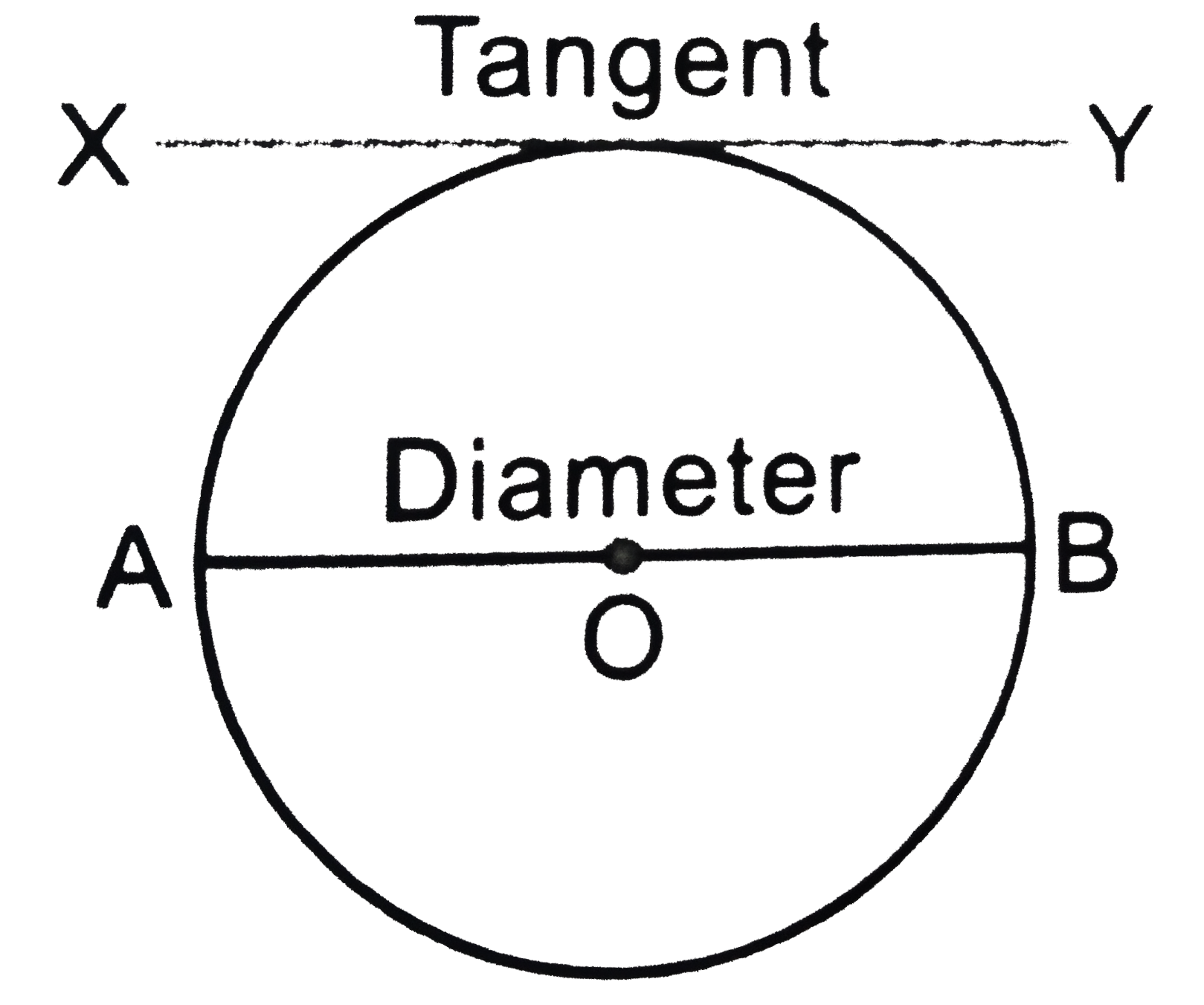
IAB=MR22
The given axis is XY, tangent to the ring in the plane of ring and parallel to its diameter AB. using the theorem of parallel axes,
IXY=IAB+MR2=12MR2+MR2=32MR2
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE B
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE C
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE A
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A52MR2B32MR2C12MR2DMR2Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
AMR2B12MR2C32MR2D72MR2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Find the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View SolutionCalculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind the moment of inertia, about a diameter, of a uniform ring of mass M = 8kg and radius a = 1m?
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-

View Solution
