Three balls of masses are arranged at the corners of an equilateral triangle of side . What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
To find the moment of inertia of the system consisting of three balls of masses 1 kg, 2 kg, and 3 kg arranged at the corners of an equilateral triangle with a side length of 1 m, we will follow these steps:
Step 1: Identify the Geometry and Masses
We have an equilateral triangle with vertices A, B, and C. The masses are:
- Mass at vertex A (m1) = 1 kg
- Mass at vertex B (m2) = 2 kg
- Mass at vertex C (m3) = 3 kg
Step 2: Find the Centroid of the Triangle
The centroid (O) of an equilateral triangle is located at a distance of L√3 from each vertex, where L is the length of the side of the triangle.
Since the side length L=1m:
- Distance from each vertex to the centroid AO=BO=CO=1√3m
Step 3: Calculate the Moment of Inertia for Each Mass
The moment of inertia I for a point mass is given by the formula:
I=m⋅r2
where m is the mass and r is the distance from the axis of rotation (centroid in this case).
For Mass at Vertex A (1 kg):
IA=m1⋅AO2=1⋅(1√3)2=1⋅13=13kg m2
For Mass at Vertex B (2 kg):
IB=m2⋅BO2=2⋅(1√3)2=2⋅13=23kg m2
For Mass at Vertex C (3 kg):
IC=m3⋅CO2=3⋅(1√3)2=3⋅13=1kg m2
Step 4: Sum the Moments of Inertia
Now, we add the individual moments of inertia to find the total moment of inertia Itotal:
Itotal=IA+IB+IC=13+23+1=13+23+33=63=2kg m2
Final Answer
The moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle is:
2kg m2
---
We have an equilateral triangle with vertices A, B, and C. The masses are:
- Mass at vertex A (m1) = 1 kg
- Mass at vertex B (m2) = 2 kg
- Mass at vertex C (m3) = 3 kg
The centroid (O) of an equilateral triangle is located at a distance of L√3 from each vertex, where L is the length of the side of the triangle.
- Distance from each vertex to the centroid AO=BO=CO=1√3m
The moment of inertia I for a point mass is given by the formula:
I=m⋅r2
where m is the mass and r is the distance from the axis of rotation (centroid in this case).
IA=m1⋅AO2=1⋅(1√3)2=1⋅13=13kg m2
IB=m2⋅BO2=2⋅(1√3)2=2⋅13=23kg m2
IC=m3⋅CO2=3⋅(1√3)2=3⋅13=1kg m2
Now, we add the individual moments of inertia to find the total moment of inertia Itotal:
Itotal=IA+IB+IC=13+23+1=13+23+33=63=2kg m2
The moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle is:
2kg m2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE B2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE C2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE A2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The PE of three objects of masses 1kg,2kg and 3kg placed at the three vertices of an equilateral triangle of side 20cm is
A25GB35GC45GD55G - Question 2 - Select One
Three point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
A(m1+m2)a24B(m2+m3)a24C(m1+m3)a24D(m1+m2+m3)a24 - Question 3 - Select One
Three identical masses, each of mass 1kg, are placed at the corners of an equilateral triangle of side l. Then the moment of inertia of this system about an axis along one side of the triangle is
A3l2Bl2C34l2D32l2
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
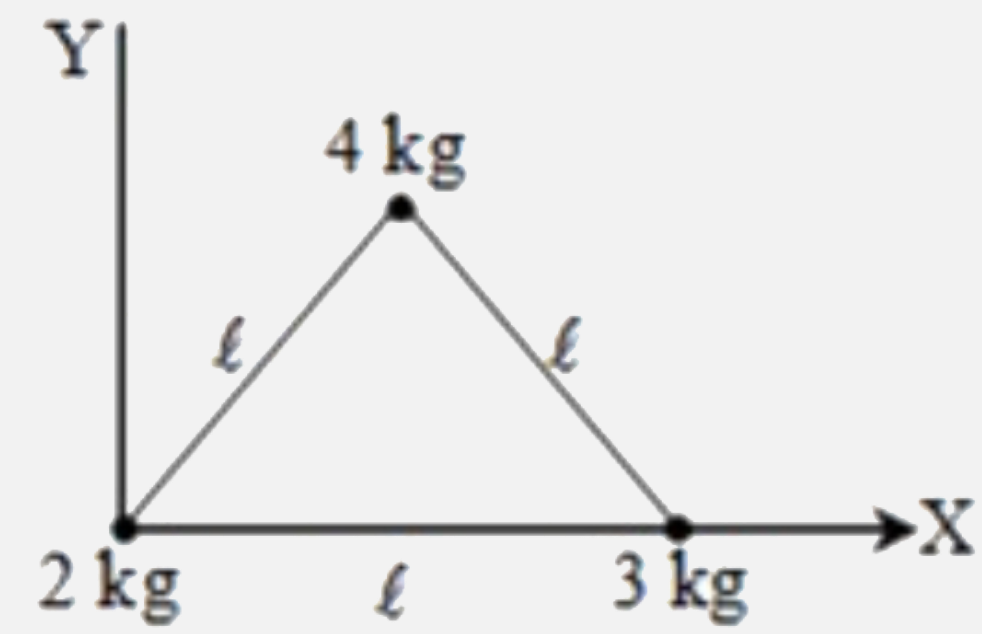 View Solution
View SolutionThree masses 1 kg, 2 kg and 3 kg are located at the vertices of an equilateral triangle of length 1. Calculate the moment of inertia of the triangle about an axis along the altitude of triangle passing through the 1 kg mass.
View SolutionThree point masses, each of mass 2kg are placed at the corners of an equilateral triangle of side 2m. What is moment of inertia of this system about an axis along one side of a triangle?
View SolutionThree point masses, each of mass m, are placed at the corner of an equilateral triangle of side 1. Then the moment of inertia of this system about an axis along one side of the triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View Solution

