Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
To find the pressure exerted below a column of water at a given depth, we can use the formula for pressure at a certain depth in a fluid:
P=P0+ρgh
Where:
- P is the pressure at depth,
- P0 is the atmospheric pressure (approximately 1.013×105Pa),
- ρ is the density of the fluid (for water, ρ=1×103kg/m3),
- g is the acceleration due to gravity (given as g=10m/s2),
- h is the depth below the surface of the fluid.
1. Identify the known values:
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=10m
2. Substitute the values into the pressure formula:
P=P0+ρgh
P=1.013×105+(1×103)(10)(10)
3. Calculate the hydrostatic pressure:
ρgh=(1×103)(10)(10)=1×103×100=1×105Pa
4. Add the atmospheric pressure:
P=1.013×105+1×105=2.013×105Pa
(ii) For depth h=30m:
1. Identify the known values (same as above, but with h=30m):
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=30m
2. Substitute the values into the pressure formula:
P=P0+ρgh
P=1.013×105+(1×103)(10)(30)
3. Calculate the hydrostatic pressure:
ρgh=(1×103)(10)(30)=1×103×300=3×105Pa
4. Add the atmospheric pressure:
P=1.013×105+3×105=4.013×105Pa
Final Answers:
- Pressure at 10 m depth: P=2.013×105Pa
- Pressure at 30 m depth: P=4.013×105Pa
- P is the pressure at depth,
- P0 is the atmospheric pressure (approximately 1.013×105Pa),
- ρ is the density of the fluid (for water, ρ=1×103kg/m3),
- g is the acceleration due to gravity (given as g=10m/s2),
- h is the depth below the surface of the fluid.
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=10m
P=P0+ρgh
P=1.013×105+(1×103)(10)(10)
ρgh=(1×103)(10)(10)=1×103×100=1×105Pa
P=1.013×105+1×105=2.013×105Pa
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=30m
P=P0+ρgh
P=1.013×105+(1×103)(10)(30)
ρgh=(1×103)(10)(30)=1×103×300=3×105Pa
P=1.013×105+3×105=4.013×105Pa
- Pressure at 10 m depth: P=2.013×105Pa
- Pressure at 30 m depth: P=4.013×105Pa
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.5
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.6
1 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.3
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionThe guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
View SolutionDensity of water is ...…(10 g cm−3/1 g cm−3).
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
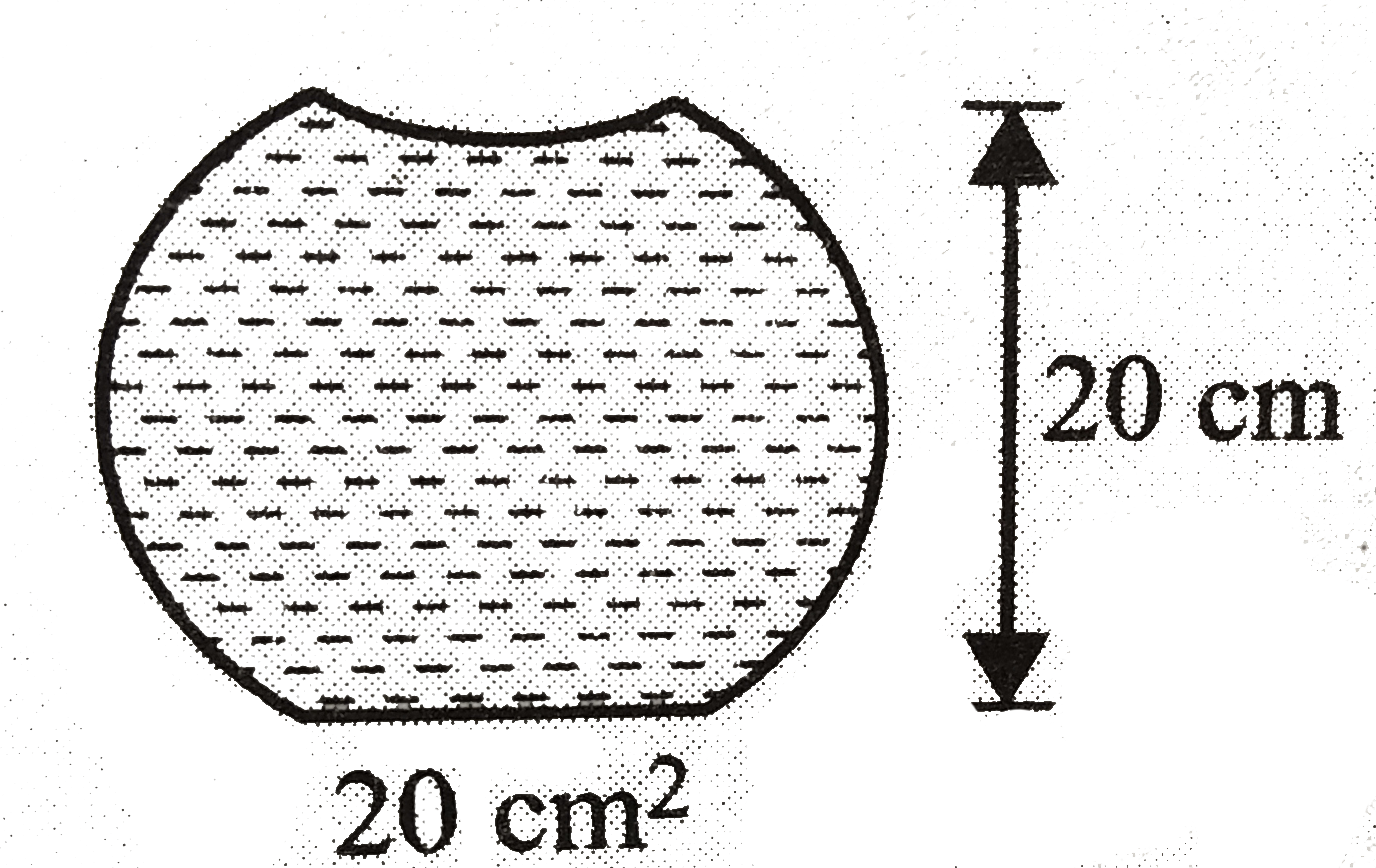
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionAt what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionA square plate of side 10 m is placed horizontally 1 m below the surface of water. The atmospheric pressure is 1.013×105Nm−2. Calculate the total thrust on the plate.
(Density of water ρ=103kgm−3,g=9.8ms−2)
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionThe pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor. (Take : density of water = 1000kg m−3,g=10m s−2 )
View Solution
