The guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
1 atm
2 atm
3 atm
4 atm
The correct Answer is:A
To find the gauge pressure exerted below a column of water at a depth of 10 meters, we can follow these steps:
Step 1: Understand the Concept of Gauge Pressure
Gauge pressure is defined as the pressure relative to the atmospheric pressure. It can be calculated using the formula:
Pgauge=ρgh
where:
- Pgauge is the gauge pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid column.
Step 2: Identify Given Values
From the problem statement:
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
- Depth of water column, h=10m
Step 3: Substitute the Values into the Formula
Now, we can substitute the known values into the gauge pressure formula:
Pgauge=ρgh
Pgauge=(1000kg/m3)×(10m/s2)×(10m)
Step 4: Calculate the Gauge Pressure
Now, we perform the multiplication:
Pgauge=1000×10×10
Pgauge=100000Pa
Step 5: Convert the Pressure to Atmospheres
Since 1atm=105Pa, we can convert the gauge pressure into atmospheres:
Pgauge=100000Pa105Pa/atm=1atm
Final Answer
Thus, the gauge pressure exerted below the column of water at a depth of 10 meters is:
Gauge Pressure=1atm
---
Gauge pressure is defined as the pressure relative to the atmospheric pressure. It can be calculated using the formula:
Pgauge=ρgh
where:
- Pgauge is the gauge pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the depth of the fluid column.
From the problem statement:
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
- Depth of water column, h=10m
Now, we can substitute the known values into the gauge pressure formula:
Pgauge=ρgh
Pgauge=(1000kg/m3)×(10m/s2)×(10m)
Now, we perform the multiplication:
Pgauge=1000×10×10
Pgauge=100000Pa
Since 1atm=105Pa, we can convert the gauge pressure into atmospheres:
Pgauge=100000Pa105Pa/atm=1atm
Thus, the gauge pressure exerted below the column of water at a depth of 10 meters is:
Gauge Pressure=1atm
Topper's Solved these Questions
Similar Questions
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View SolutionWhat is the pressure in an ocean at a depth of 1000 m, if the density of water is 1.024×103kgm3. Atmospheric pressure P.=1.01×105 Pa.
View SolutionThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
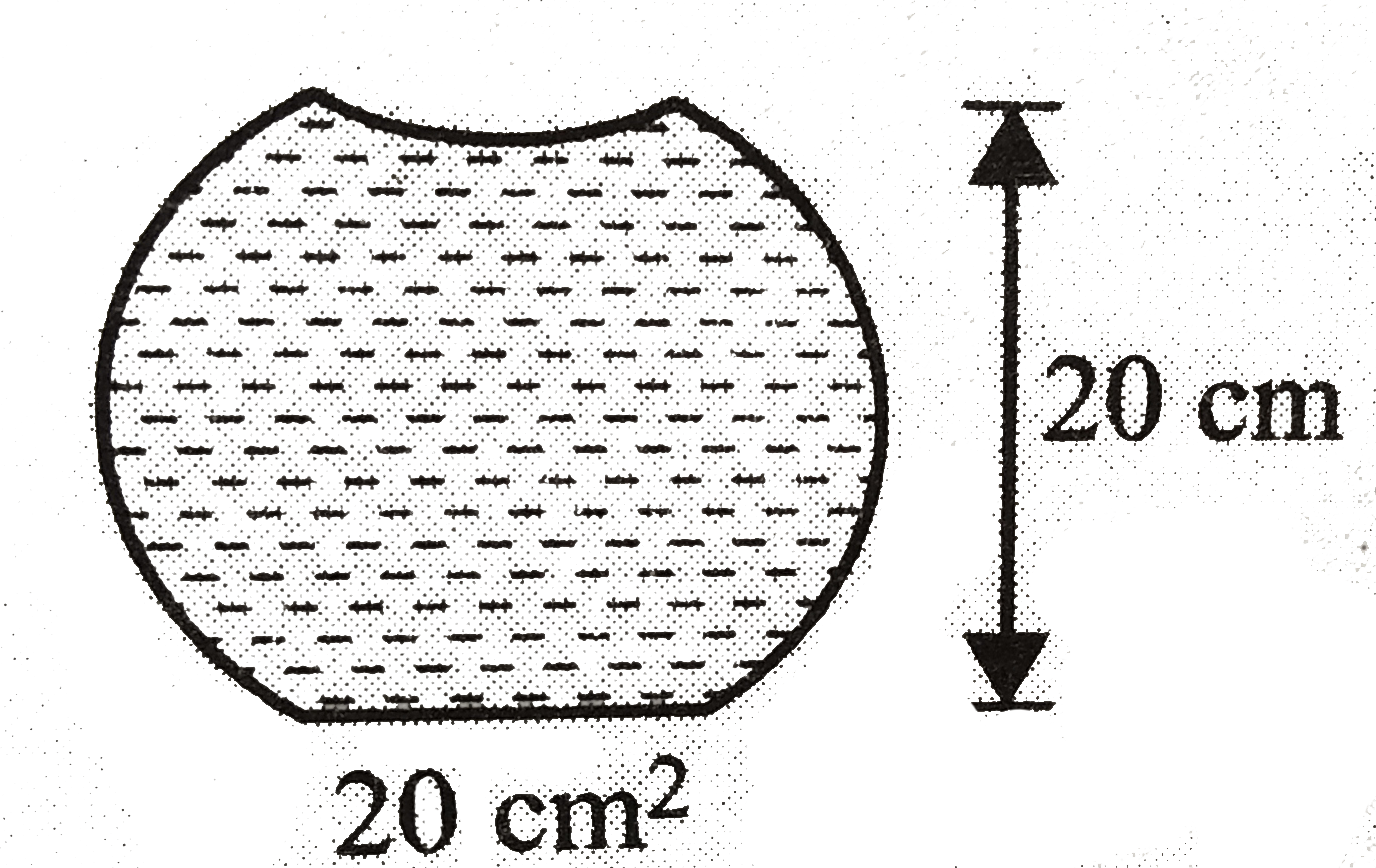
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
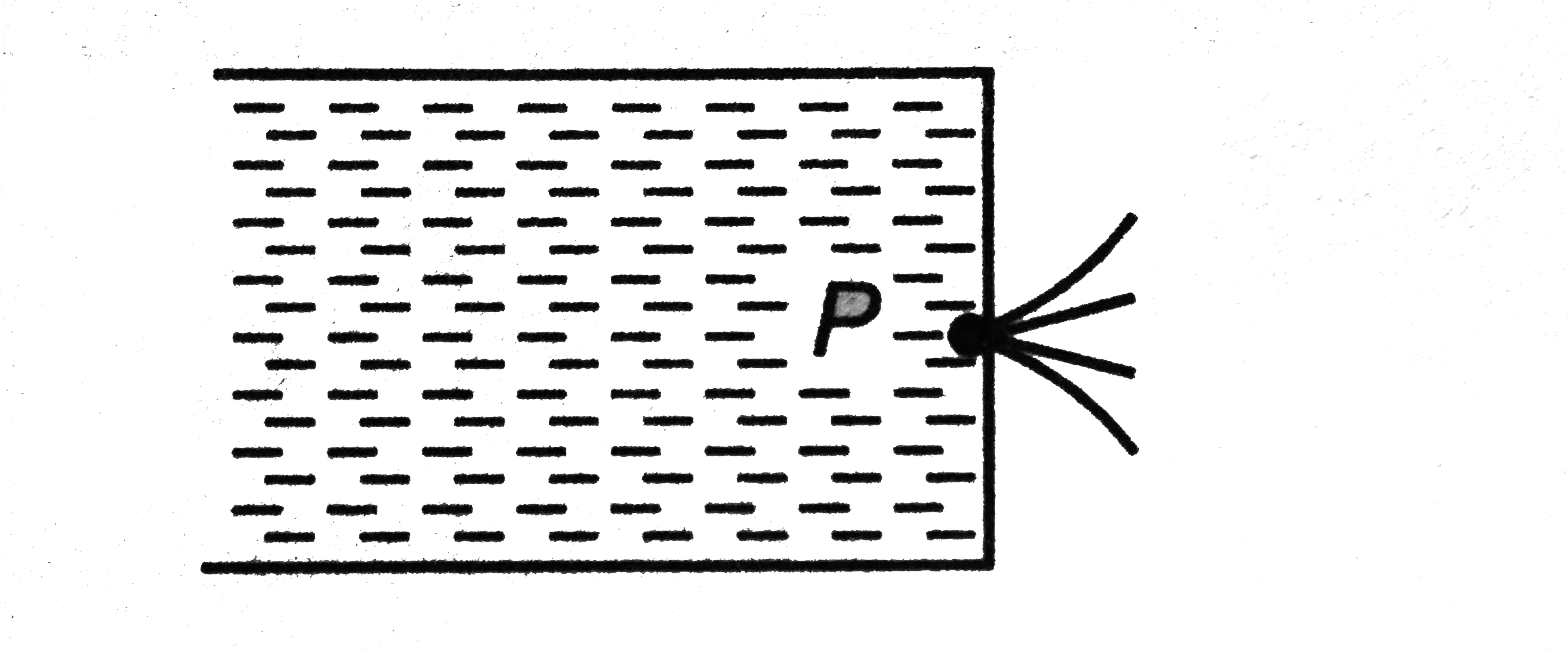
View SolutionA leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was 5×105N/m2. If the density of water is 1000kg/m3 the initial velocity with which water gushes out is approximately
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
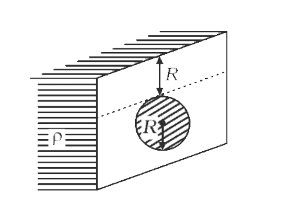
View SolutionFind the hydrostatic force (in kN) acting on the circular patch of radius R.(R=1m,g=10m/s2 , atmospheric pressure = 10 ^(5 ) Pa )
View SolutionIn a carburator of an engine, aire is drawn from atmosphere through section A with a velocity of 10m/s. The narrow section B is connected to a petrol tank as shown. The minimum ratio of area of cross section A to area of cross section B, so that the petrol can just enter the carburator tube is √66x. Then the value of x is : (density of petrol =1000kg/m3, density of air =2kg/m3,g=10m/s2 atmospheric pressure =105 Pa and assume density of air remain constant)

View SolutionAt what depth below the surface of water will pressure be equal to twice the atmospheric pressure ? The atmospheric pressure is 10Ncm−2 , density of water is 103kgm−3 and g=9.8ms−2.
View Solution
