Find the ratio of the fundamental tone frequencies of two identical strings after one of them was stretched by η1=2.0% and the other, by η2=4.0%. The tension is assumed to be proportional to the elongation.
We have n=1nl√Tm=12l√TlM Where M= total mass of the wire. When the wire is streched,total mass of the wire remains consta. For the first wire the new length =l+η1l and for the record wire, the length is l=η2l. Also T1=α(η1l) where α is a constant and T2=α(η2l). Subtituting in the above formula.
v1=123(l+η1l)√(αη1l)(l+η1l)M
v1=123(l+η2l)√(αη2l)(l+η2l)M
∴v2v1=1+η11+η2√η2η1.1+η2l1+η1
v2v1=√η2(1+η1)η2(1+η2)=√0.04(1+0.02)0.02(1+0.04)=1.4
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Two srting of the same length, radius and material are stretched by η1=2% and η2=4% respectively.Find the ratio of frequency of the strings .The tension of the string may be assumed to be proportional to the elongation
View SolutionHow much has a filament diameter decreased due to evaporation if the mainteenance of the previous temperature required an increase of voltage by η=1.0%. The amount of heat transferred from the filament to surrounding space is assumed to be proportional to the filament surface area.
View Solution
Knowledge Check
Fundamental frequency of two identical strings x and y are 450Hz and 300Hz resp. then find the ratio of tension in string x and y will be
A(2/3^1/2B44078C(4/3)^1/2D(3/2^1/2The fundamental frequency of a stretched string is V0. If the length is reduced by 35% and tension increased by 69% the fundamental frequency will be
A0.2V0B0.5V0C2.0V0D1.6V0Two identical stringed instruments have frequency 100 Hz . If tension in one of them is increased by 4% and they are sounded together then the number of beats in one second is
A1B8C4D2
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
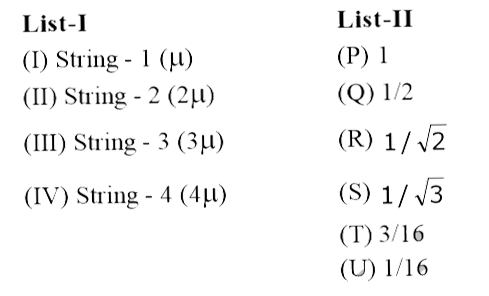
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -
View SolutionParticle 1 moving with velocity v=10m/s experienced a head-on collision with a stationary particle 2 of the same mass. As a result of the collision, the kinetic energy of the system decreased by η=1.0%. Find the magnitude and direction of the velocity of particle 1 after the collision.
View SolutionIf f1andf2 be the fundamental frequencies of the two segments into which a stretched string is divided by means of a bridge , then find the original fundamental frequency f of the complete string.
View SolutionFour wires of identical lengths, diameters and materials are stretched on a sonometer box. The ratio of their tension 1:4:9:16. The ratio of their fundamental frequencies is
View SolutionTwo identical wires have a fundamental frequency of 100Hz, when kept under the same tension . If the tension of one of the wires is increased by 21% , the number of beats produced is
View Solution
