Find the ratio of the fundamental tone frequencies of two identical strings after one of them was stretched by η1=2.0% and the other, by η2=4.0%. The tension is assumed to be proportional to the elongation.
To find the ratio of the fundamental tone frequencies of two identical strings that have been stretched by different percentages, we can follow these steps:
Step 1: Understand the relationship between frequency, tension, and length
The fundamental frequency f of a string is given by the formula:
f=12L√Tm
where:
- L is the length of the string,
- T is the tension in the string,
- m is the mass per unit length of the string.
Step 2: Determine the effect of stretching on tension
When a string is stretched, its tension T increases. The tension is assumed to be proportional to the elongation. If a string is stretched by a percentage η, the new tension can be expressed as:
T=k⋅η⋅L0
where k is a constant and L0 is the original length of the string.
Step 3: Define the fractional increase in length
Let:
- For string 1, the fractional increase in length f1=η1=0.02 (2%).
- For string 2, the fractional increase in length f2=η2=0.04 (4%).
Step 4: Write the frequency expressions for both strings
For string 1:
f1=12L0√k⋅f1⋅L0m
For string 2:
f2=12L0√k⋅f2⋅L0m
Step 5: Establish the ratio of frequencies
The ratio of the frequencies can be expressed as:
f1f2=√f1√f2⋅1√1+f1⋅√1+f21
Substituting the values:
f1f2=√0.02√0.04⋅1+0.041+0.02
Step 6: Simplify the expression
Calculating the square roots:
f1f2=√0.02√0.04⋅1.041.02=√0.020.2⋅1.041.02
=√22⋅1.041.02
Step 7: Calculate the final ratio
Now, we can compute the numerical values:
f1f2=√1.042⋅1.02=√1.042.04
Calculating this gives us the final ratio.
Final Answer
After performing the calculations, we find:
f1f2≈0.7
The fundamental frequency f of a string is given by the formula:
f=12L√Tm
where:
- L is the length of the string,
- T is the tension in the string,
- m is the mass per unit length of the string.
When a string is stretched, its tension T increases. The tension is assumed to be proportional to the elongation. If a string is stretched by a percentage η, the new tension can be expressed as:
T=k⋅η⋅L0
where k is a constant and L0 is the original length of the string.
Let:
- For string 1, the fractional increase in length f1=η1=0.02 (2%).
- For string 2, the fractional increase in length f2=η2=0.04 (4%).
For string 1:
f1=12L0√k⋅f1⋅L0m
For string 2:
f2=12L0√k⋅f2⋅L0m
The ratio of the frequencies can be expressed as:
f1f2=√f1√f2⋅1√1+f1⋅√1+f21
f1f2=√0.02√0.04⋅1+0.041+0.02
Calculating the square roots:
f1f2=√0.02√0.04⋅1.041.02=√0.020.2⋅1.041.02
=√22⋅1.041.02
Now, we can compute the numerical values:
f1f2=√1.042⋅1.02=√1.042.04
Calculating this gives us the final ratio.
After performing the calculations, we find:
f1f2≈0.7
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective
24 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct
144 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
Knowledge Check
The product of two numbers is 2.0016. If one of them is 0.72, find the other number.
A2.078B2.0078C2.78D0.278
Four wires of identical lengths, diameters and materials are stretched on a sonometer box. The ratio of their tension 1:4:9:16. The ratio of their fundamental frequencies is
View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
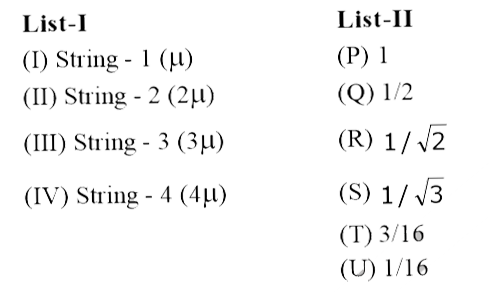
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -
View SolutionIf f1andf2 be the fundamental frequencies of the two segments into which a stretched string is divided by means of a bridge , then find the original fundamental frequency f of the complete string.
View SolutionIf f1andf2 be the fundamental frequencies of the two segments into which a stretched string is divided by means of a bridge , then find the original fundamental frequency f of the complete string.
View SolutionA string of length 2x is stretched by 0.1 x and the velocity of a transverse wave along it is v. When it is stretched by 0.4x , the velocity of the wave is
View SolutionIf the length of a stretched string is shortened by 40% and the tension is increased by 44%, then the ratio of the final and initial fundamental frequencies is
View SolutionFour wires of identical lengths, diameters and materials are stretched on a sonometer box. What is the ratio of the tensions in the wires such that the ratio of their fundamental frequencies is 4:3:2:1?
View Solution
