Find the relation between the three wavelengths λ1,λ2andλ3 from the energy level diagram shown below.
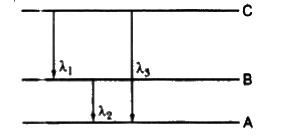
Ec−EB=hcλ1 ...(1)
EB−EA=hcλ2 ...(2)
EC−EA=hcλ3 ...(3)
Adding (1) and (2), we have
EC−EA=hcλ1+hcλ2 ...(4)
From (3) and (4), we have
hcλ3=hcλ1+hcλ2⇒1λ3=1λ1+1λ2
⇒λ3=λ1λ2λ1+λ2
Topper's Solved these Questions
- CBSE EXAMINATION PAPER - 2016 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER - 2016 EXERCISE - SECTION - E
17 Videos
- CBSE EXAMINATION PAPER - 2016 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER - 2016 EXERCISE - SECTION - B
5 Videos
- CBSE BOARD EXAMNATION PAPER (2017 )BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE BOARD EXAMNATION PAPER (2017 )EXERCISE - SECTION E
12 Videos
- CBSE Examination Paper Delhi–2014BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE Examination Paper Delhi–2014EXERCISE - SET-III (Questions Uncommon to set-I and II)
9 Videos
Similar Questions
The energies E1 and E2 of two radiations are 25eV and 50eV respectively. The relation between their wavelengths, i.e., λ1 and λ2 will be.
View SolutionThe energy that should be added to an electron to reduce its de Broglie wavelength from λ to λ2 is (Considering E to the energy of electron when its de Broglie wavelength is λ )
View Solution
Knowledge Check
The relation between wavelength (λ) and angular wave number (k) of a wave is
Ak=2πλBk=λ2πCk=1λDk=2πλDue to transitions among its first three energy levels, hydrogenic atom emits radiation at three discrete wavelengths λ1,λ2, and λ3(λ1<λ2<λ3). Then
Aλ1=λ2+λ3Bλ1+λ2=λ3C1/λ1+1/λ2=1/λ3D1/λ1=1/λ2+1/λ3Which curve shows the relation ship between the energy R and the wavelength λ of a photon of electromagnetic radiation?
A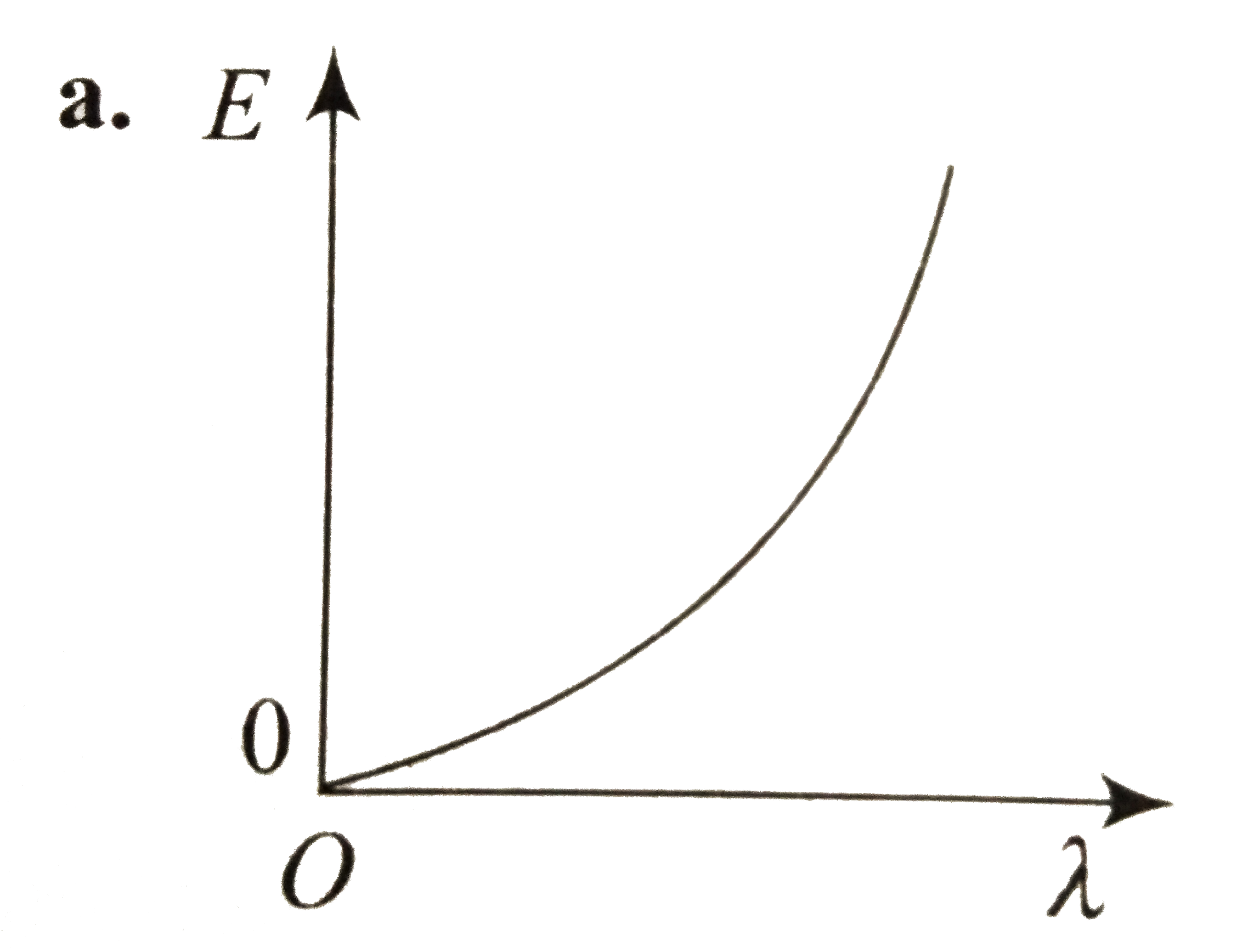 B
B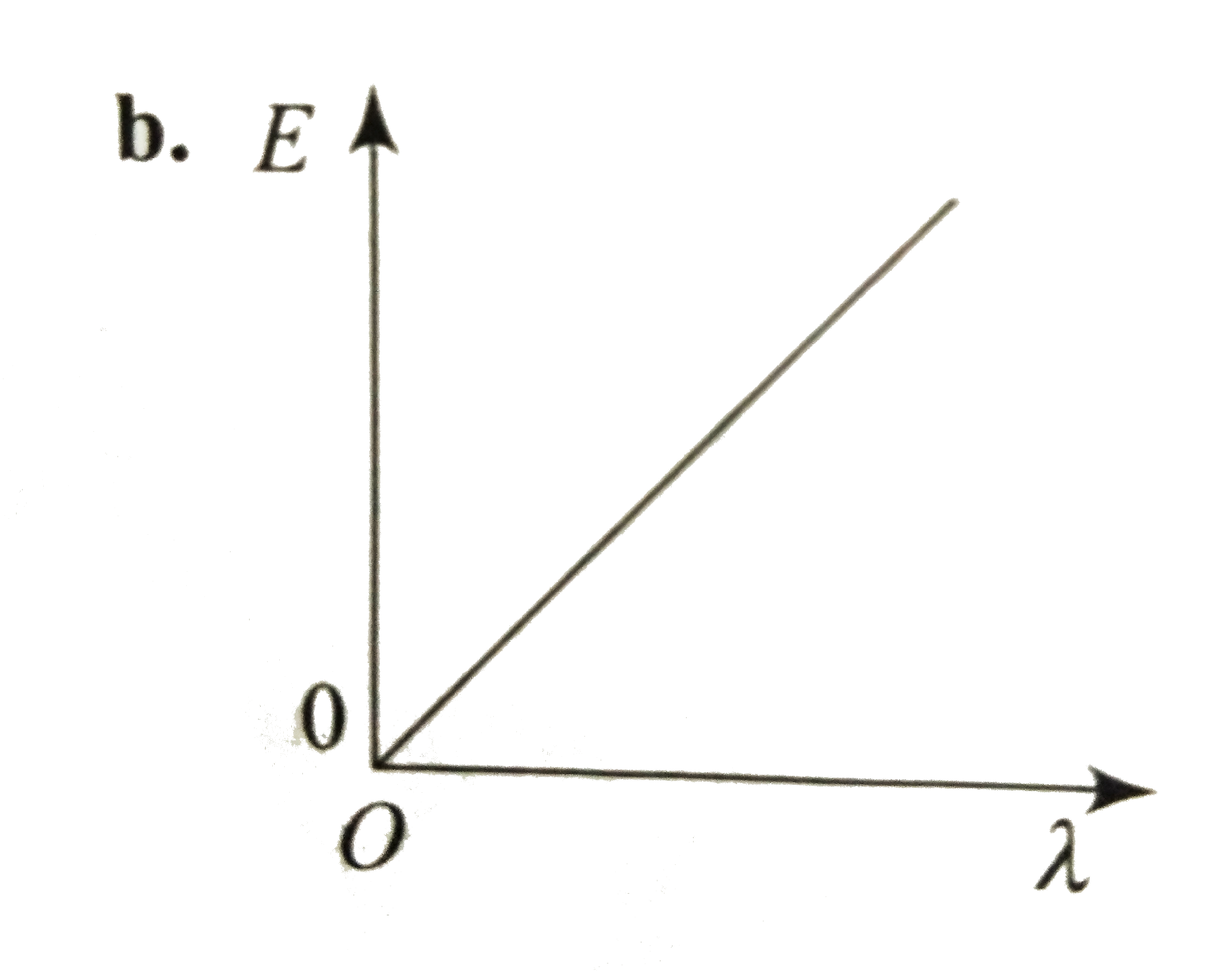 C
C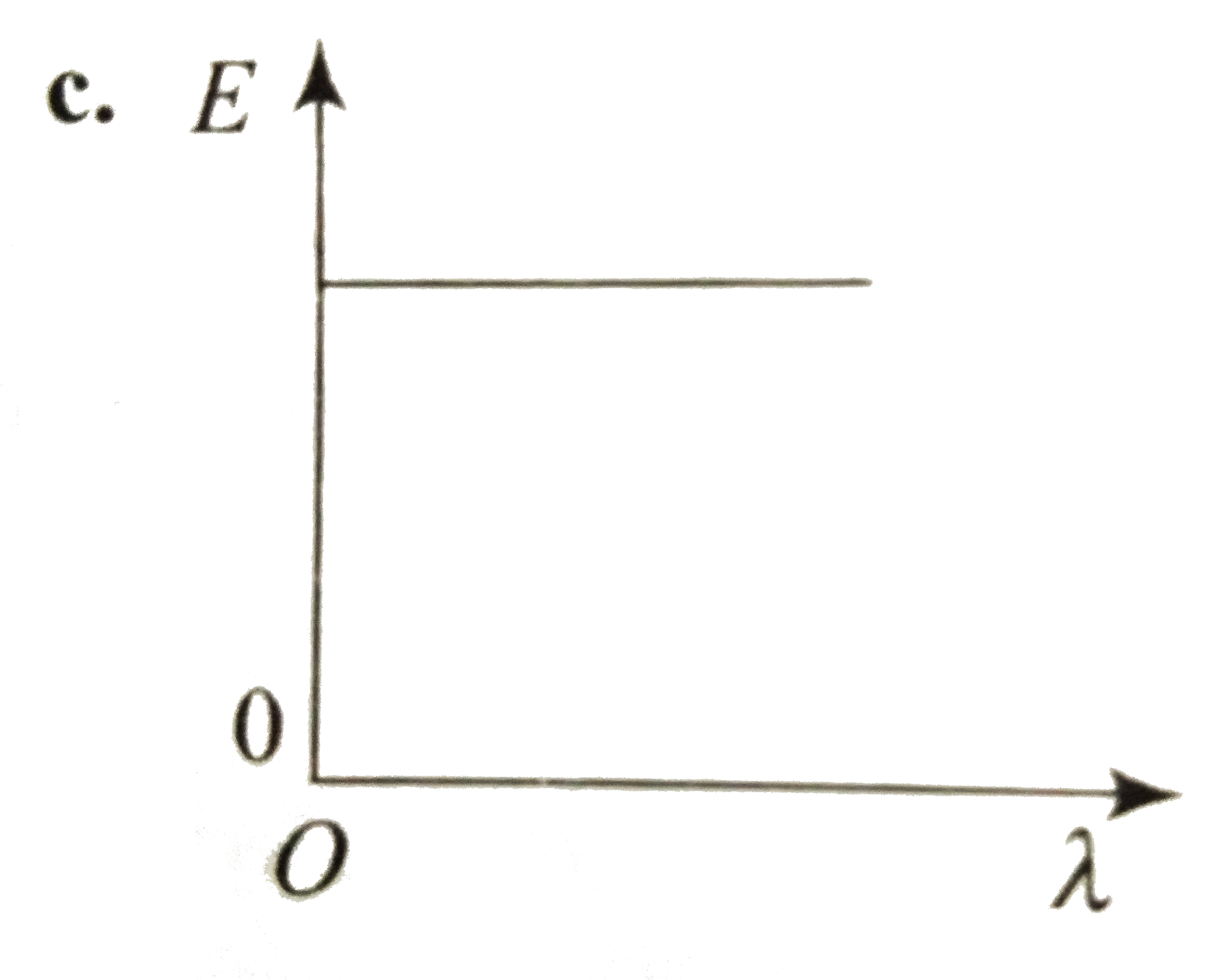 D
D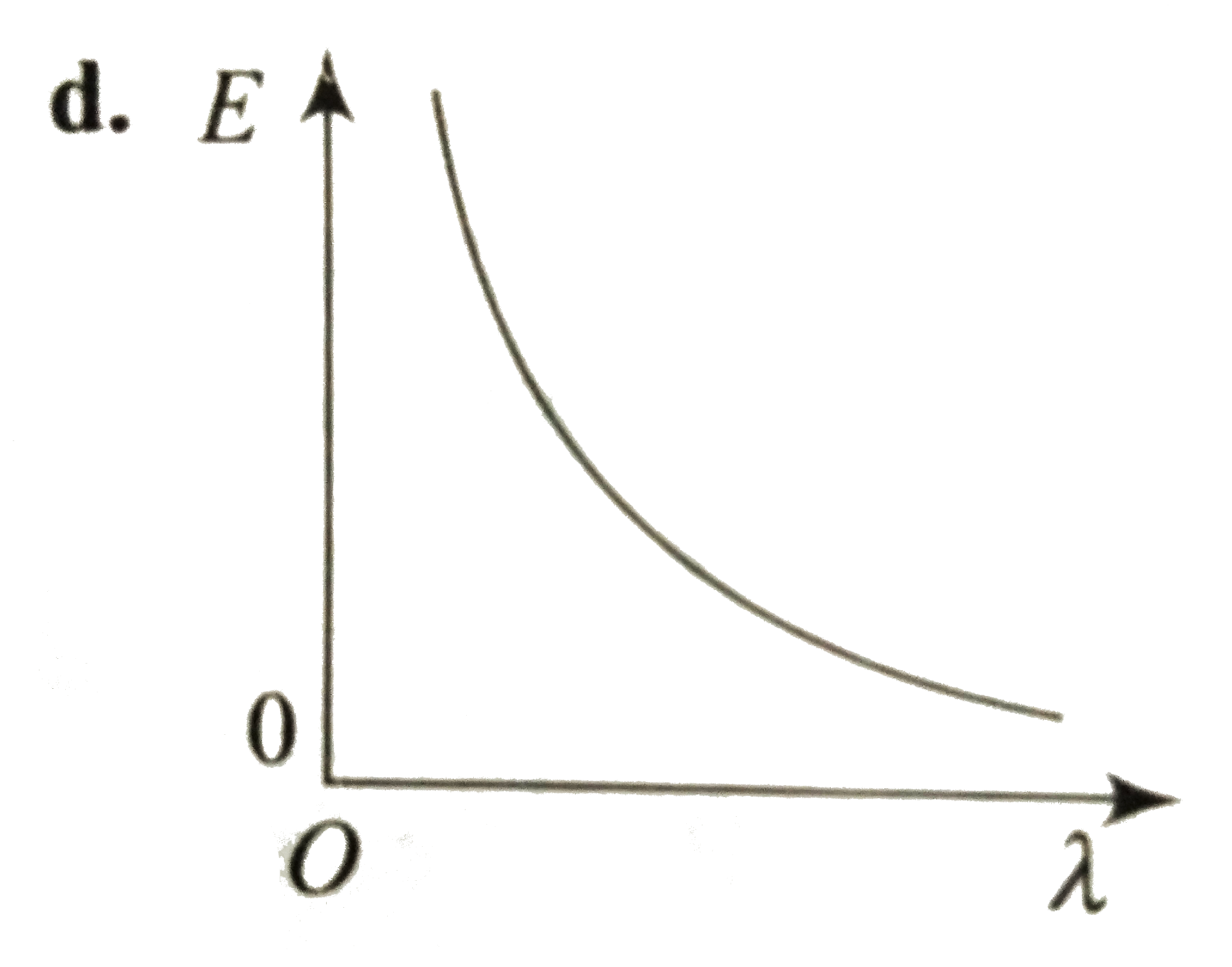
Certain substance emits only the wavelengths λ1,λ2,λ3 and λ4 when it is at a high temperature, it will absorb only the following wavelengths
View SolutionThe energies E1 and E2 of two radiations are 25eV and 50eV respectively. The relation between their wavelengths, i.e., λ1 and λ2 will be.
View SolutionA dye absorbs a photon of wavelength λ and re-emits the same energy into two photns of wavelength λ1 and λ2 respectively. The wavelength λ is related to λ1 and λ2 as :
View SolutionNeglecting the mass variation with velocity , the ratio of the wavelength (λeλp) associated with an electron (λe) having a kinetic energy E and wavelength associated with a Photon (λp) having kinetie energy 4E is
View SolutionThe wavelength λe of ann electron and λp of a photon of same energy E are related by
View Solution
