An ac source of voltage V=V0sinωt is connected to a series combination of L, C and R. Use the phasor diagram to obtain expressions for impedance of the circuit and phase with the voltage. What is circuit in this condition called?
To solve the problem step by step, we will analyze the series combination of an inductor (L), a capacitor (C), and a resistor (R) connected to an AC source with voltage given by V=V0sin(ωt). We will derive the expressions for impedance and phase difference using a phasor diagram.
Step 1: Understanding the Circuit
We have a series circuit consisting of:
- An inductor with inductance L
- A capacitor with capacitance C
- A resistor with resistance R
The voltage across the circuit is given by V=V0sin(ωt).
Step 2: Phasor Representation
In AC circuits, we can represent voltages and currents as phasors. The voltage across the resistor VR, inductor VL, and capacitor VC can be represented as:
- VR=IR (in phase with current)
- VL=IXL (where XL=ωL, leads the current by 90 degrees)
- VC=IXC (where XC=1ωC, lags the current by 90 degrees)
Step 3: Phasor Diagram
In the phasor diagram:
- The voltage across the resistor VR is along the horizontal axis.
- The voltage across the inductor VL is represented vertically upwards (90 degrees ahead of current).
- The voltage across the capacitor VC is represented vertically downwards (90 degrees behind current).
Step 4: Net Voltage Calculation
The total voltage V in the circuit can be calculated using the vector sum of the voltages:
V=VR+VL−VC
This can be expressed as:
V=IR+IXL−IXC
Combining the reactances:
V=I(R+j(XL−XC))
Step 5: Impedance Calculation
The impedance Z of the circuit is defined as the ratio of the voltage to the current:
Z=VI=R+j(XL−XC)
The magnitude of the impedance can be calculated using:
|Z|=√R2+(XL−XC)2
Step 6: Phase Angle Calculation
The phase angle ϕ between the voltage and the current can be calculated using:
tan(ϕ)=XL−XCR
Thus, the phase angle is given by:
ϕ=tan−1(XL−XCR)
Step 7: Type of Circuit
In this condition, where both inductive and capacitive reactances are present, the circuit is called an RLC series circuit.
Summary of Results
- Impedance: Z=√R2+(XL−XC)2
- Phase Angle: ϕ=tan−1(XL−XCR)
- Type of Circuit: RLC series circuit
We have a series circuit consisting of:
- An inductor with inductance L
- A capacitor with capacitance C
- A resistor with resistance R
In AC circuits, we can represent voltages and currents as phasors. The voltage across the resistor VR, inductor VL, and capacitor VC can be represented as:
- VR=IR (in phase with current)
- VL=IXL (where XL=ωL, leads the current by 90 degrees)
- VC=IXC (where XC=1ωC, lags the current by 90 degrees)
In the phasor diagram:
- The voltage across the resistor VR is along the horizontal axis.
- The voltage across the inductor VL is represented vertically upwards (90 degrees ahead of current).
- The voltage across the capacitor VC is represented vertically downwards (90 degrees behind current).
The total voltage V in the circuit can be calculated using the vector sum of the voltages:
V=VR+VL−VC
This can be expressed as:
V=IR+IXL−IXC
Combining the reactances:
V=I(R+j(XL−XC))
The impedance Z of the circuit is defined as the ratio of the voltage to the current:
Z=VI=R+j(XL−XC)
The magnitude of the impedance can be calculated using:
|Z|=√R2+(XL−XC)2
The phase angle ϕ between the voltage and the current can be calculated using:
tan(ϕ)=XL−XCR
Thus, the phase angle is given by:
ϕ=tan−1(XL−XCR)
In this condition, where both inductive and capacitive reactances are present, the circuit is called an RLC series circuit.
- Impedance: Z=√R2+(XL−XC)2
- Phase Angle: ϕ=tan−1(XL−XCR)
- Type of Circuit: RLC series circuit
Topper's Solved these Questions
- CBSE EXAMINATION PAPER - 2016 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER - 2016 EXERCISE - SECTION - C
16 Videos
- CBSE BOARD EXAMNATION PAPER (2017 )BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE BOARD EXAMNATION PAPER (2017 )EXERCISE - SECTION E
12 Videos
- CBSE Examination Paper Delhi–2014BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE Examination Paper Delhi–2014EXERCISE - SET-III (Questions Uncommon to set-I and II)
9 Videos
Similar Questions
(i) An a.c. source of voltage V=Vmsinωt is connected to a series combination of L, C and R. Use the phasor diagram to obtain expressions for impedance of the circuit and phase angle between voltage and current. Find the condition when current will be in phase with the voltage. What is the circuit in this condition called ?
(ii) In a series LR circuit XL=R and power factor of the circuit is P1 . When capacitor with capacitance C such that XL=XC is put in series, the power factor becomes P2 . Calculate P1/P2
View Solution(i) An a.c. Source of voltage V=V0 sin ωt is connected to a series combination of L,C and R . Use the phasor diagram to obtain expression for impedance of the circuit and phase angle between voltage and current . Find the condition when current will be phase with the voltage . What is the circuit in this condition called ?
(ii) In a series LR circuit XL=R and power factor of the circuit is P1. When capacitor which capacitance C such that XL=XC is put in series , the power factor becomes P2 .Calculate P1/P2

View Solution
Knowledge Check
An ac source of voltage V=Vmsinωt is connected across the resistance R as shown in figure. The phase relation between current and voltage for this circuit is
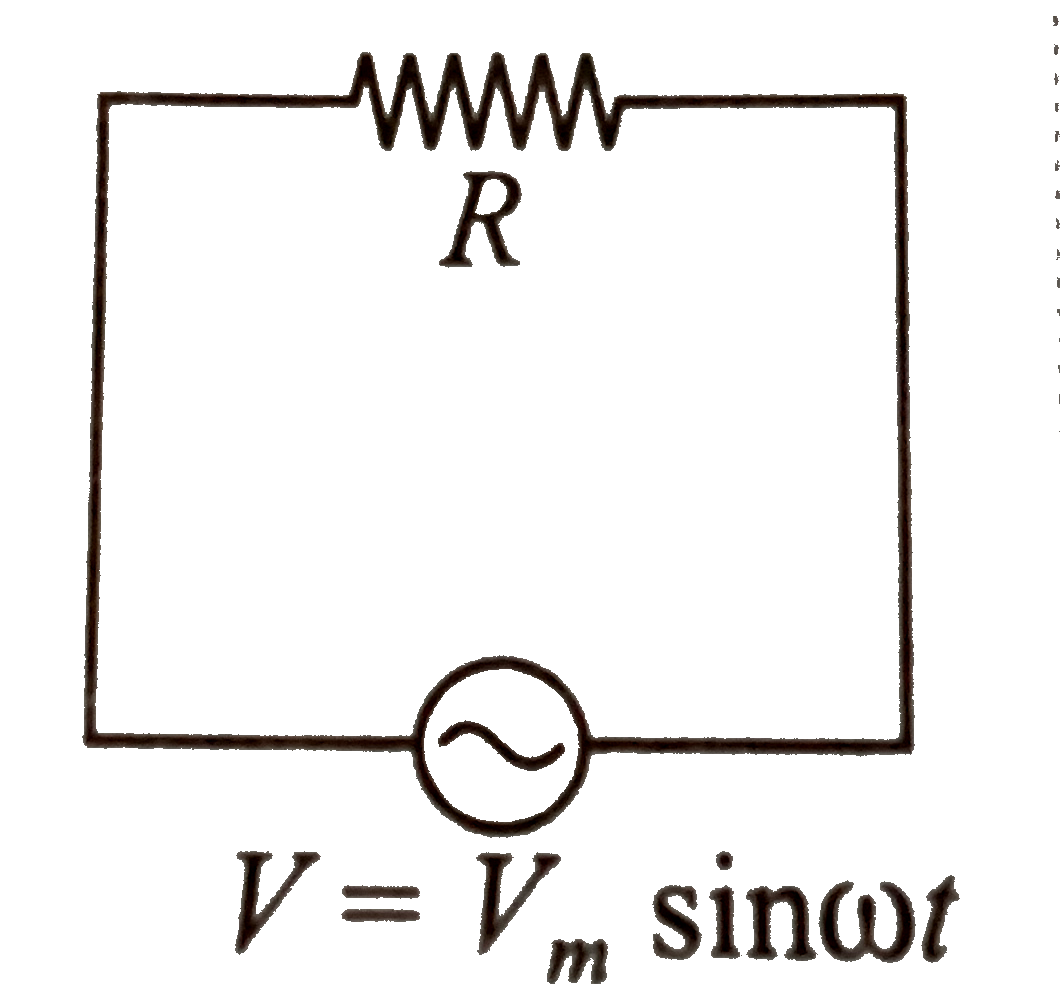 Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
Aboth are in phaseBboth are out of phase by 90∘Cboth are out of phase by 120∘Dboth are out of phase by 180∘
(a) An AC source of voltage V=V0sinωt is connected across a series combination of an inductor a capacitor and a resistor . Use the phasor diagram to obtain the expression for the impedance of the circuit and phase angle between the voltage and the current.
(b) A capacitor of unknown capacitance a resistor of 100 Ω and an inductor of self - inductance L =(4/π2) henry are in series connected to an AC source of 200 V and 50 Hz . Calculate the value of the capacitance and the current that flows in the circuit when the current is in phase with the voltage .
View SolutionA source of a.c. voltage V=Vmsinωt is connected to a series combination of a capacitor C and a resistor R. Draw the phasor diagram and use it to obtain the expression for (i) impedance of the circuit, and (ii) phase angle.
View Solution(a) An a.c. source of voltage V=Vmsinωt is connected across a series combination of an inductor, a capacitor and a resistor. Use the phasor diagram to obtain the expression for
(i) impedance of the circuit, and
(ii) phase angle between the voltage and the current
(b) A capacitor of unknown capacitor, a resistor of 100Ω and an inductor of self-inductance L=4π2H are connected in series to an a.c. source of 200 V and 50 Hz. Calculate the value of the capacitance and the current that flows in the circuit when the current is in phase with the voltage.
View SolutionWith the help of a phasor diagram find an expression for impedance (Z) in a series L-C-R circuit.
View SolutionAn a.c. source, of voltage V=Vmsinωt , is applied across a series LCR circuit. Draw the phasor diagram for the circuit when the
(i) capacitive reactance exceeds the inductive reactance,
(ii) inductive reactance exceeds the capacitive reactance.
View SolutionDraw the phasor diagram for a series RC circuit connected to an a.c. source.
View Solutiona) Derive the expression for the current flowing in an ideal capacitor and its reactance when connected to an ac source of voltage V=V0sinωt
b) Draw its phasor diagram.
c) If resistance is added in series to capacitor what changes will occur in the current flowing in the circuit and phase angle between voltage and current.
View Solution
