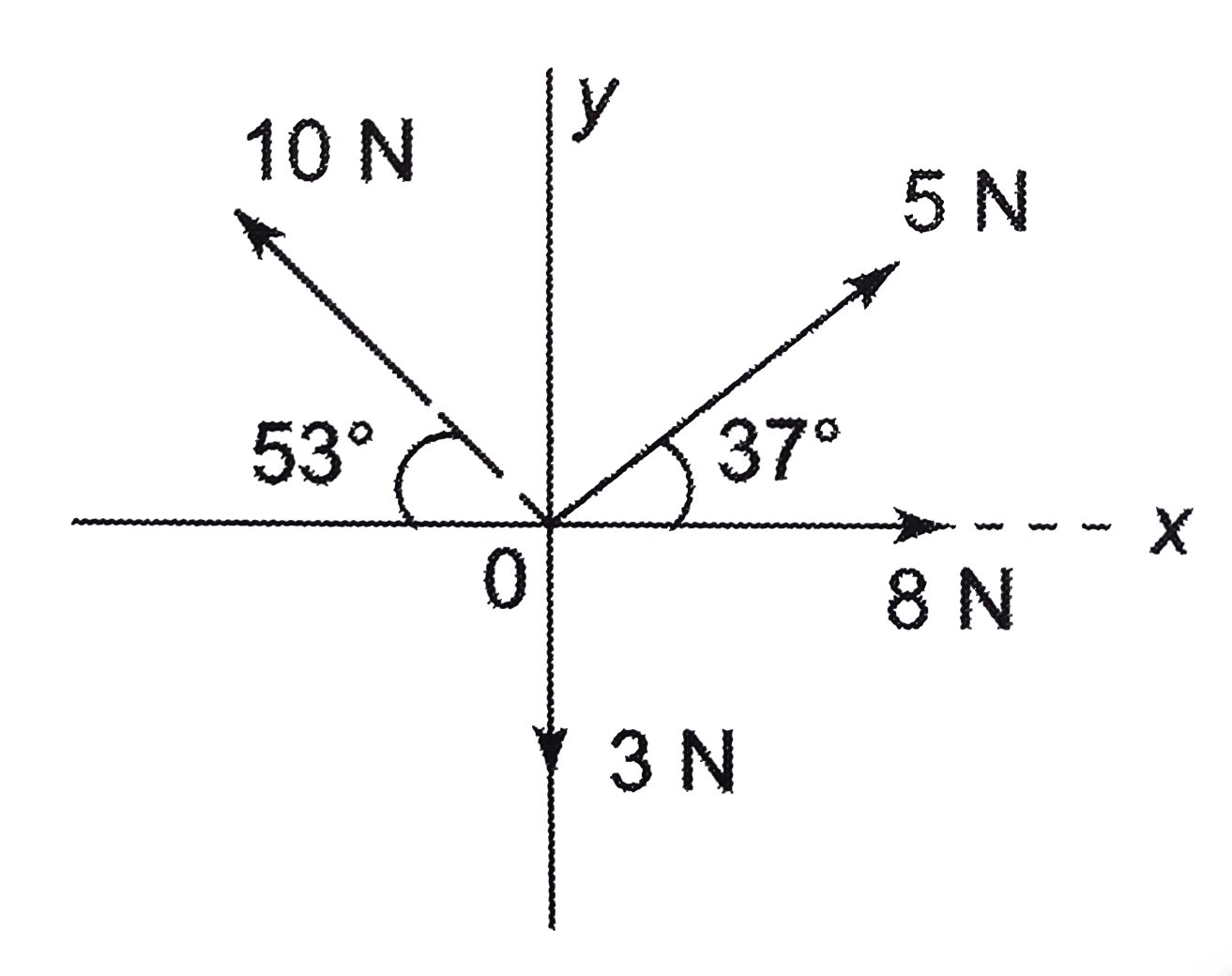
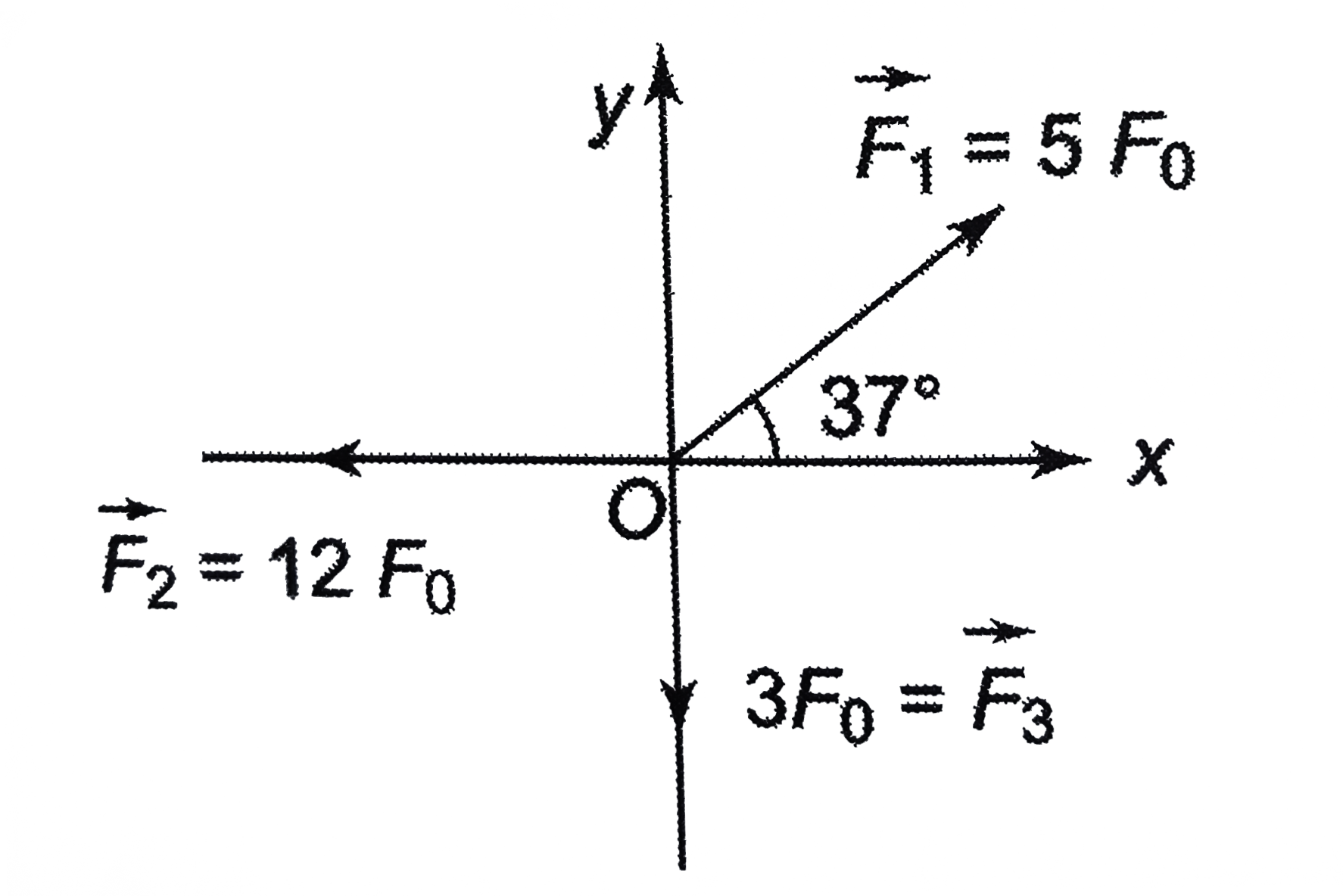
Find the resultant of −→F1+−→F2−−→F3(sin37∘=35,cos37∘=45)
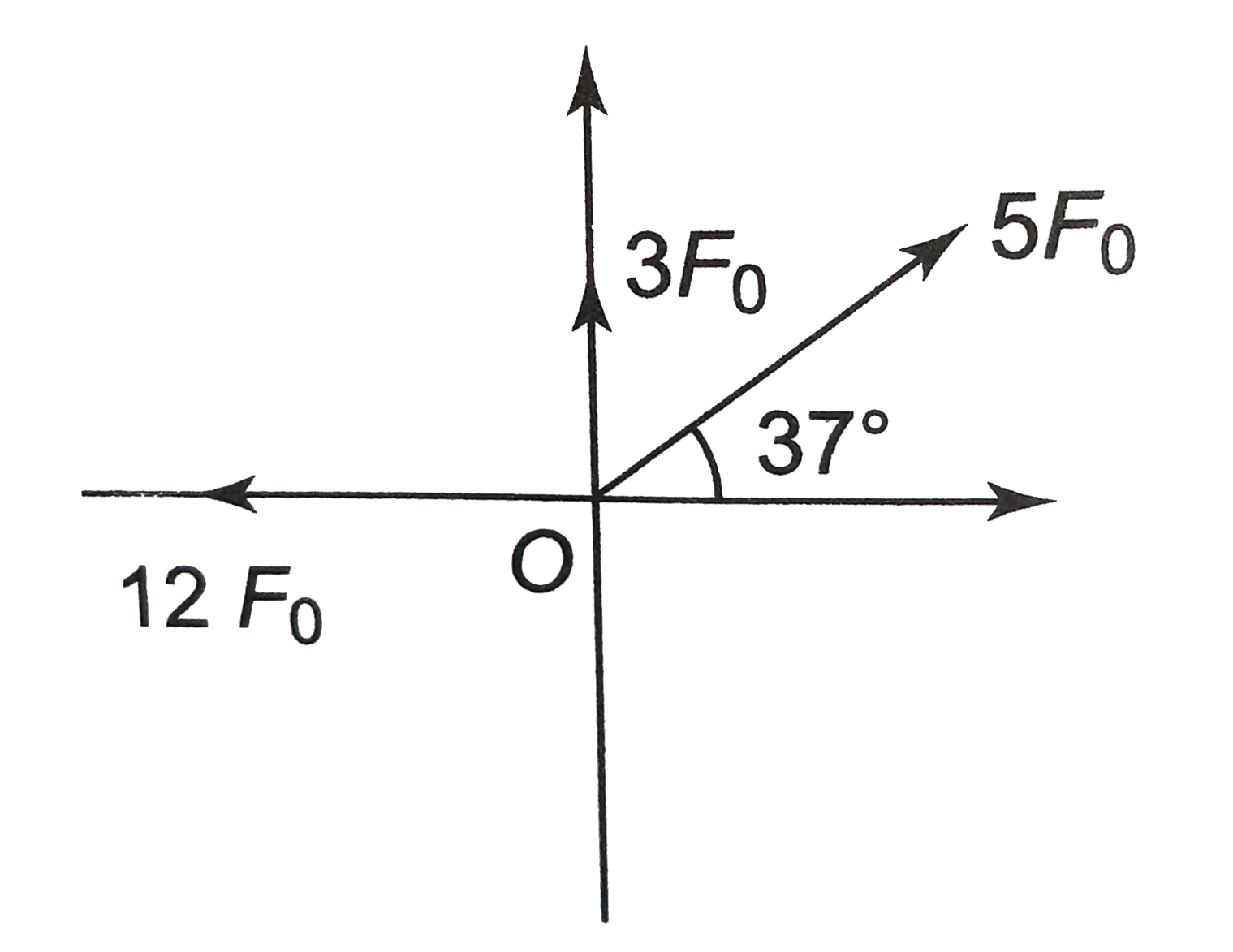
→R=−→F1+−→F2−−→F3=−→F1+−→F2+(−−→F3)
Reverse the direction of −→F3 and add vectors by the component approach.
Fx=5F0cos37∘−12F0
=5F0×45−12F0=−8F0
Fy=5F0sin37∘+3F0
=3F0×35+3F0=6F0
F=√(8F0)2+(6F0)2=10F0
tanθ=6F08F0=34⇒θ=37∘
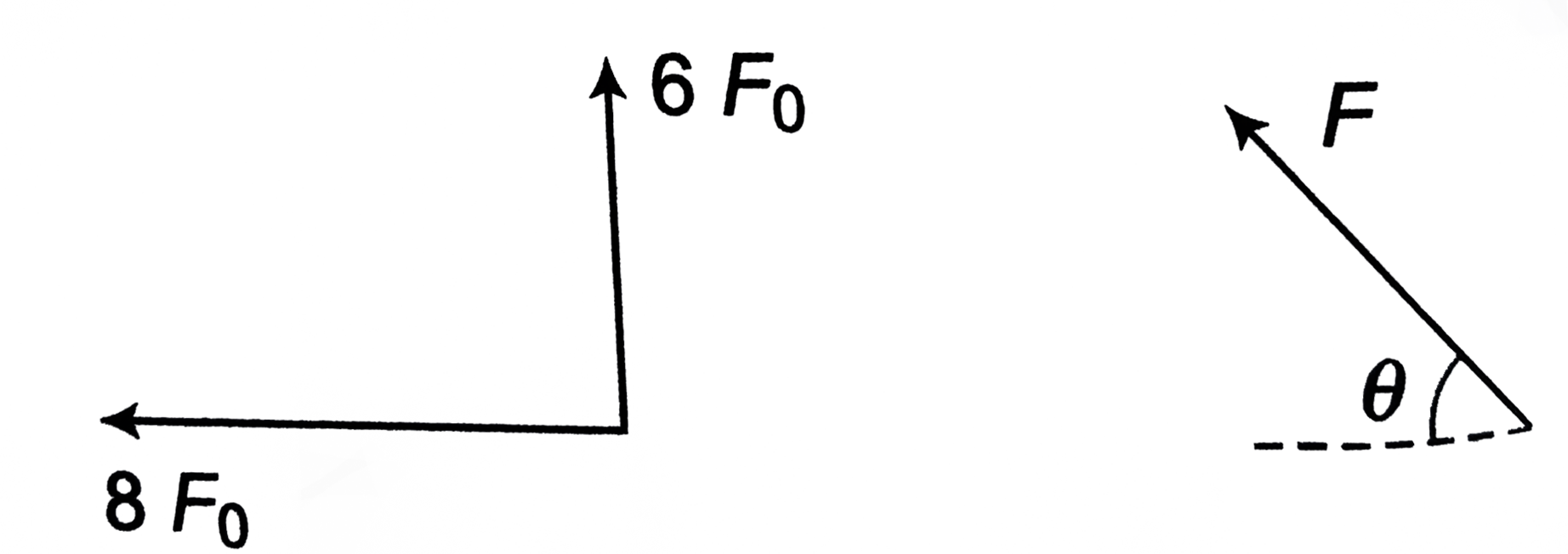
Topper's Solved these Questions
Similar Questions
Knowledge Check
Five forces →F1,→F2,→F3,→F4 , and →F5 , are acting on a particle of mass 2.0kg so that is moving with 4m/s2 in east direction. If →F1 force is removed, then the acceleration becomes 7m/s2 in north, then the acceleration of the block if only →F1 is action will be:
A16m/s2B√65ms2C√260ms2D√233ms2A body placed in free space, is simultaneously acted upon by three forces −→F1,−→F2 and −→F3. The body is in equilibrium and the forces −→F1 and −→F2 are known ot be 36 N due north and 27 N due east respectively. Which of the following best describes the force −→F3?
A36N due southB53N due 60∘ south of eastC45N due 53∘ south of westD45N due 37∘ north of west.A moving perticle of mass m is acted upon by five forces →F1,→F2,→F3,→F4 and →F5. Forces →F2 and →F3 are conservative and their potential energy funcations are U and W respectively. Speed of the particle changes from Va to Vb when it moves from position a to b. Choose the correct option :
ASum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−WaBSum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−Wa+12m(V2b−V2a)CSum of work done by all five forces =12m(V2b+V2a)DSum of work done by →F2 and →F3=(Ub+Wb)−(Ua+Wa)
A particle, in equilibrium, is subjected to four forces →F1,→F2,→F3 and →F4, →F1=−10ˆk,→F2=u(413ˆi−1213ˆj+313ˆk),→F3=v(−413ˆi−1213ˆj+313ˆk),→F4=w(cosθˆi+sinθˆj) then find the values of u,v and w
View SolutionThe base vectors →a1,→a2,→a3 are given in terms vectors →b1,→b2,→b3, →a1=2→b1+3→b1−→b1,→a2=→a1−2→b2+2→b3,→a3=−2→b1+→b2−2→b3,if →F1=3→b1−→b2+2→b3, Express →F in terms of →a1,→a2,→a3
View SolutionIf three forces −→F1,+−→F2and−→F3 are represented by three sides of a triangle and −→F1+−→F2=−−→F3 , then these three forces are concurrent forces and satisfy the condition for equilibrium .
Statement II : A triangle made up of three forces →F1,→F2and→F3 as sides taken in the same order ,satisfy the condition for translatory equilibrium . In the light of the above statements ,choose the most appropriate answer from the options given below :
View SolutionExamine for coplanarity of the following sets of points
3→a+2→b−5→c,3→a+8→b+5→c,−3→a+2→b+→c,→a+4→b−3→c.
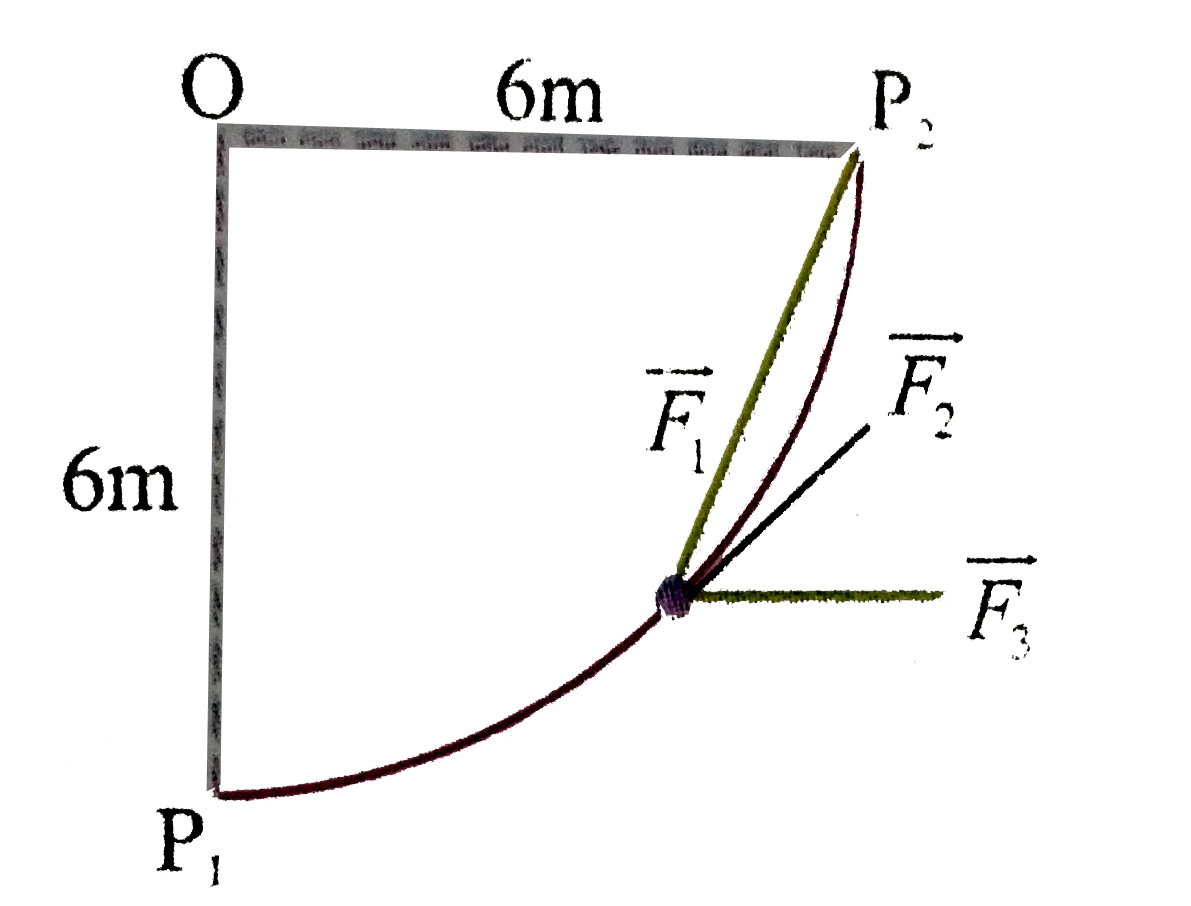
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View Solution