If three forces −→F1,+−→F2and−→F3 are represented by three sides of a triangle and −→F1+−→F2=−−→F3 , then these three forces are concurrent forces and satisfy the condition for equilibrium .
Statement II : A triangle made up of three forces →F1,→F2and→F3 as sides taken in the same order ,satisfy the condition for translatory equilibrium . In the light of the above statements ,choose the most appropriate answer from the options given below :
Both Statement I and Statement II are false
Statement I is true but Satement II is false.
Both Statement I and Statement II are true.
Statement I is false but Statement II is true
To solve the given problem, we need to analyze the statements regarding the forces represented by the sides of a triangle and their conditions for equilibrium.
1. Understanding the Forces and Triangle Representation:
- We have three forces →F1,→F2, and →F3 that are represented by the sides of a triangle.
- According to the problem, the forces are arranged such that →F1+→F2=−→F3.
2. Applying the Equilibrium Condition:
- For three forces to be in equilibrium, the vector sum of the forces must be zero. This means:
→F1+→F2+→F3=0
- From the given condition →F1+→F2=−→F3, we can rearrange this to:
→F1+→F2+→F3=0
- This confirms that the forces are indeed in equilibrium.
3. Analyzing Statement I:
- The first statement claims that the three forces are concurrent and satisfy the condition for equilibrium.
- Since we have established that the sum of the forces is zero, Statement I is true.
4. Analyzing Statement II:
- The second statement asserts that a triangle formed by the forces →F1,→F2, and →F3 satisfies the condition for translatory equilibrium.
- Translatory equilibrium means that the net force acting on a body is zero, which is satisfied by the condition we derived.
- Therefore, Statement II is also true.
5. Conclusion:
- Both statements are true, thus the correct answer is that both statements I and II are true.
Final Answer:
Both statements I and II are true.
- We have three forces →F1,→F2, and →F3 that are represented by the sides of a triangle.
- According to the problem, the forces are arranged such that →F1+→F2=−→F3.
- For three forces to be in equilibrium, the vector sum of the forces must be zero. This means:
→F1+→F2+→F3=0
- From the given condition →F1+→F2=−→F3, we can rearrange this to:
→F1+→F2+→F3=0
- This confirms that the forces are indeed in equilibrium.
- The first statement claims that the three forces are concurrent and satisfy the condition for equilibrium.
- Since we have established that the sum of the forces is zero, Statement I is true.
- The second statement asserts that a triangle formed by the forces →F1,→F2, and →F3 satisfies the condition for translatory equilibrium.
- Translatory equilibrium means that the net force acting on a body is zero, which is satisfied by the condition we derived.
- Therefore, Statement II is also true.
- Both statements are true, thus the correct answer is that both statements I and II are true.
Both statements I and II are true.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A)
81 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS
30 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Statement 1: Three force →f1, →f2 and →f3 are acted at vertices of a triangular body such that →f1+→f2=−→f3 and these force are concurrent forces,
Statement 2: It explain translations equilibrium
View SolutionWhat are concurrent forces ? Obtain a condition for the equilibrium of three concurrent forces
View Solution
Knowledge Check
Three concurrent force of the same magnitude are in equilibrium. What is the angle between the forces? Also name the triangle formed by the forces as sides.
A60∘ equilateral triangleB120∘, equilateral triangleC30∘, an isosceles triangleD120∘, an obtuse angled triangleThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
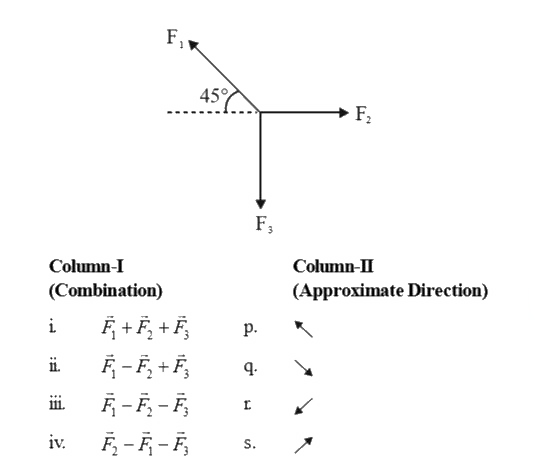
Now match the given columns and select the correct option from the codes given below.Ai-p,ii-q,iii-r,iv-sBi-s,ii-r,iii-q,iv-pCi-q,ii-r,iii-p,iv-sDi-r,ii-s,iii-p,iv-qTwo forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2
If →a,→band→c are represented by three sides of equilateral triangle taken in same order.
P.T.→a+→b+→c=→0 .
View SolutionIf →a, →b, →c represent the sides of a triangle taken in order, then write the value of →a+→b+→c
View SolutionWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
View SolutionWhen force −→F1,−→F2,−→F3…...−→Fn act on a particle , the particle remains in equilibrium . If −→F1 is now removed then acceleration of the particle is
View SolutionTwo forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View Solution
