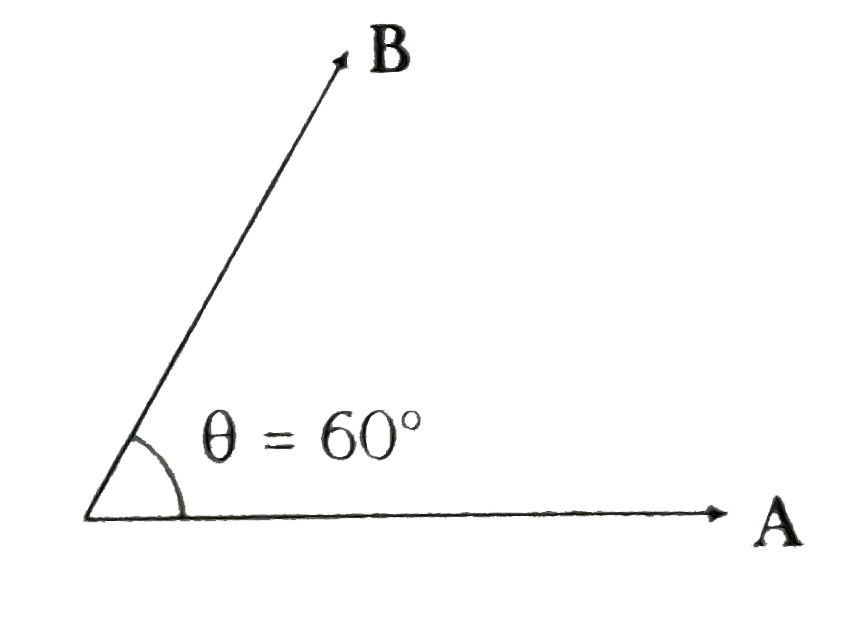
Find the sum of vector A and B as shown in the figure ,also find the direction of sum vector. Given A=4unit and B=3unit .

A
√35unit , α=tan−1(0.472)=25.3∘
B
√25unit , α=tan−1(0.472)=25.3∘
C
√37unit , α=tan−1(0.472)=25.3∘
D
√37unit , α=tan−1(1)=45∘
Video Solution
Text Solution
The correct Answer is:C
According to the question ,we draw the following figure .
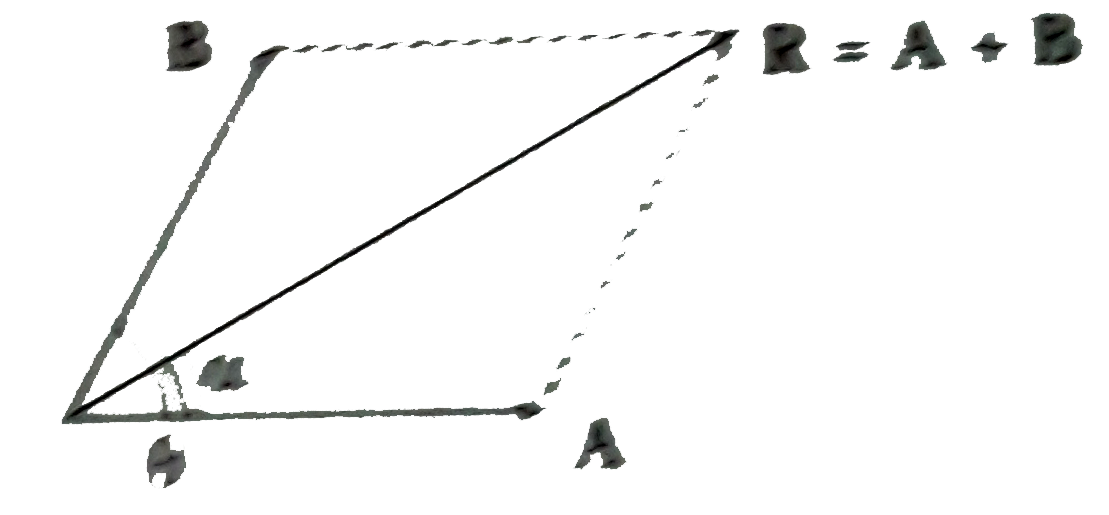
Resultant of the vectors A and B
R=√A2+B2+2ABcosθ
=√16+9+2×4×3cos60∘=√37unit
∴Direction of the sum vector ,
tanα=BsinθA+Bcosθ=3sin60∘4+3cos60∘=0.472
α=tan−1(0.472)=25.3∘
Thus resultant of |A|and|B| is √37 unit at angle 25.3∘ from A in the direction shown in figure .
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the sum of vector A and B as shown in the figure ,also find the direction of sum vector. Given A=4unit and B=3unit .
 A√35unit , α=tan−1(0.472)=25.3∘B√25unit , α=tan−1(0.472)=25.3∘C√37unit , α=tan−1(0.472)=25.3∘D√37unit , α=tan−1(1)=45∘
A√35unit , α=tan−1(0.472)=25.3∘B√25unit , α=tan−1(0.472)=25.3∘C√37unit , α=tan−1(0.472)=25.3∘D√37unit , α=tan−1(1)=45∘Find the subraction of vector A and B as shown in the figure , also find the direction of subtraction vector ,Given A=4 unit and b=3 unit .
 A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘
A=√19unit 60B=√24unit 45∘C=√17unit 46.1∘D=√13unit 46.1∘Find A+B and A-B in the diagram shown in figure. Given A=4 units and B=3 units.
 .A√ 30,√ 22 unitsB√ 40,√ 28C√ 37,√ 15 unitsD√ 37,√ 13
.A√ 30,√ 22 unitsB√ 40,√ 28C√ 37,√ 15 unitsD√ 37,√ 13
Find the unit vector in the direction of sum of vectors →a=ˆ2i−ˆj+ˆk and →b=2ˆj+ˆk.
View SolutionFind the unit vector in the direction of the vector →a=ˆi+ˆj+2ˆk.
View SolutionFind unit vector in the direction of vector →a=2ˆi+3ˆj+ˆk.
View SolutionFind a unit vector in the direction of vector →A=(ˆi−2ˆj+ˆk)
View SolutionFind a unit vector in the direction of vector: →a=2ˆi+3ˆ+ˆk
View Solution
