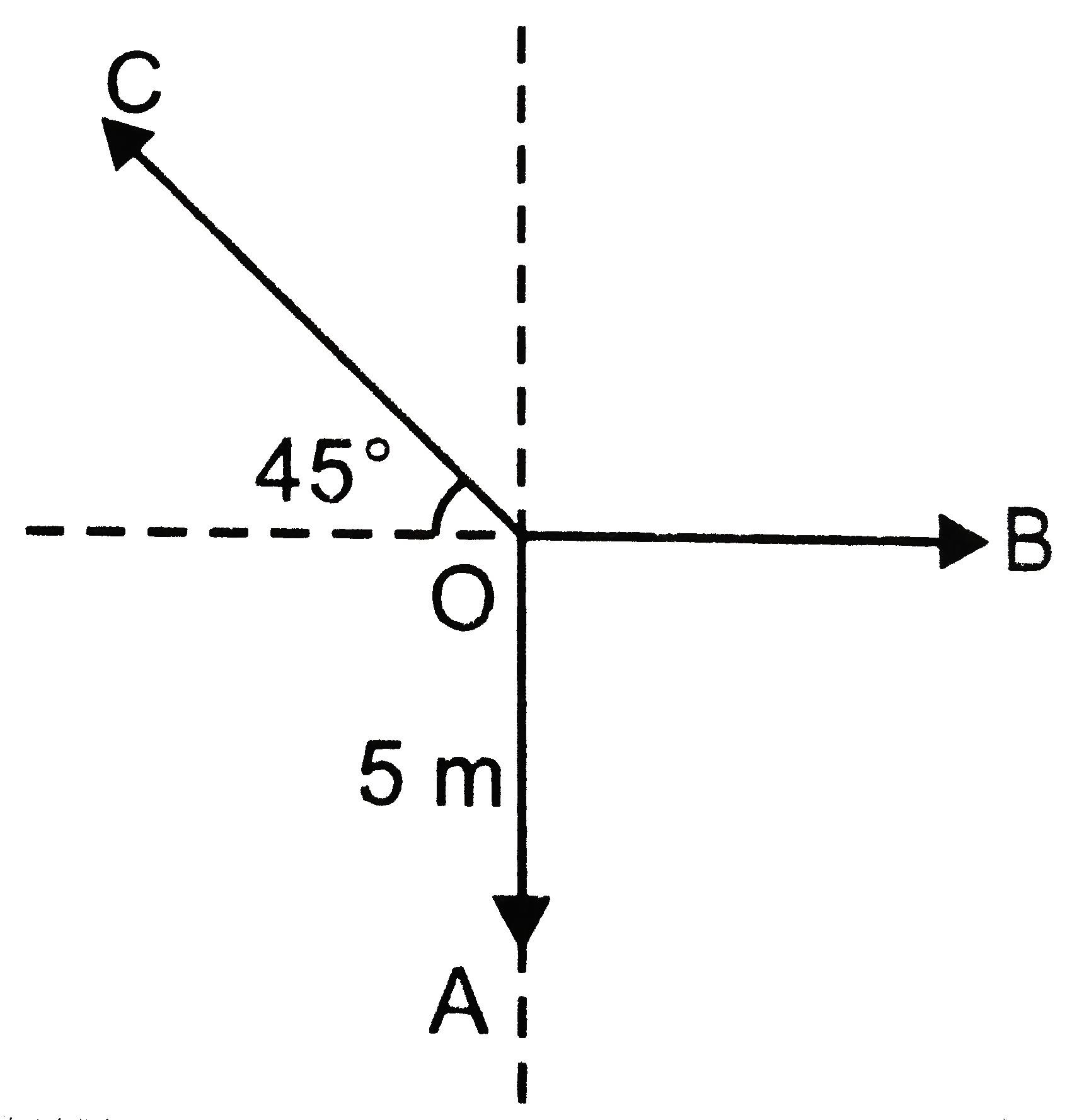
The sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
To solve the problem of finding the magnitudes of the vectors →OB and →OC given that the sum of three vectors →OA, →OB, and →OC is zero, we can follow these steps:
Step 1: Define the vectors
- The vector →OA has a magnitude of 5 units and is directed downwards along the negative y-axis. Therefore, we can express it as:
→OA=−5^j
Step 2: Define the vector →OB
- Let the magnitude of vector →OB be OB and assume it is directed along the positive x-axis. Thus, we can express it as:
→OB=OB^i
Step 3: Define the vector →OC
- Let the magnitude of vector →OC be OC. Since it is in the xy-plane and forms an angle of 45 degrees with the negative x-axis, we can express its components as:
→OC=−OCcos(45∘)^i+OCsin(45∘)^j
Since cos(45∘)=sin(45∘)=1√2, we can write:
→OC=−OC√2^i+OC√2^j
Step 4: Set up the equation for the sum of the vectors
- According to the problem, the sum of the three vectors is zero:
→OA+→OB+→OC=0
Substituting the expressions we have for each vector:
−5^j+OB^i+(−OC√2^i+OC√2^j)=0
Step 5: Combine the components
- Combining the i and j components:
- For the i-component:
OB−OC√2=0(1)
- For the j-component:
−5+OC√2=0(2)
Step 6: Solve the equations
- From equation (2):
OC√2=5⟹OC=5√2
- Substitute OC into equation (1):
OB−5√2√2=0⟹OB−5=0⟹OB=5
Final Results
- The magnitudes of the vectors are:
|→OB|=5 units
|→OC|=5√2 units
- The vector →OA has a magnitude of 5 units and is directed downwards along the negative y-axis. Therefore, we can express it as:
→OA=−5^j
- Let the magnitude of vector →OB be OB and assume it is directed along the positive x-axis. Thus, we can express it as:
→OB=OB^i
- Let the magnitude of vector →OC be OC. Since it is in the xy-plane and forms an angle of 45 degrees with the negative x-axis, we can express its components as:
→OC=−OCcos(45∘)^i+OCsin(45∘)^j
Since cos(45∘)=sin(45∘)=1√2, we can write:
→OC=−OC√2^i+OC√2^j
- According to the problem, the sum of the three vectors is zero:
→OA+→OB+→OC=0
Substituting the expressions we have for each vector:
−5^j+OB^i+(−OC√2^i+OC√2^j)=0
- Combining the i and j components:
- For the i-component:
OB−OC√2=0(1)
- For the j-component:
−5+OC√2=0(2)
- From equation (2):
OC√2=5⟹OC=5√2
- Substitute OC into equation (1):
OB−5√2√2=0⟹OB−5=0⟹OB=5
- The magnitudes of the vectors are:
|→OB|=5 units
|→OC|=5√2 units
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 1
6 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
Similar Questions
The sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
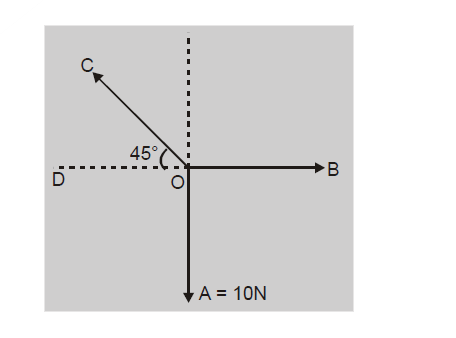
(ii) What is the magnitude of vector −−→OC ?
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector −−→OB?<br>(b)Wˆisthemagnitudeofthe→−−→r vec (OC) ?
View Solution
Knowledge Check
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of theseThe magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8What is the magnitude of the sum of the vectors →P=3ˆIand→Q=4ˆj ?
A3B4C5D7
A vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionThe resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionGiven that →A+→B+→C=→0. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionFind the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

View Solution
