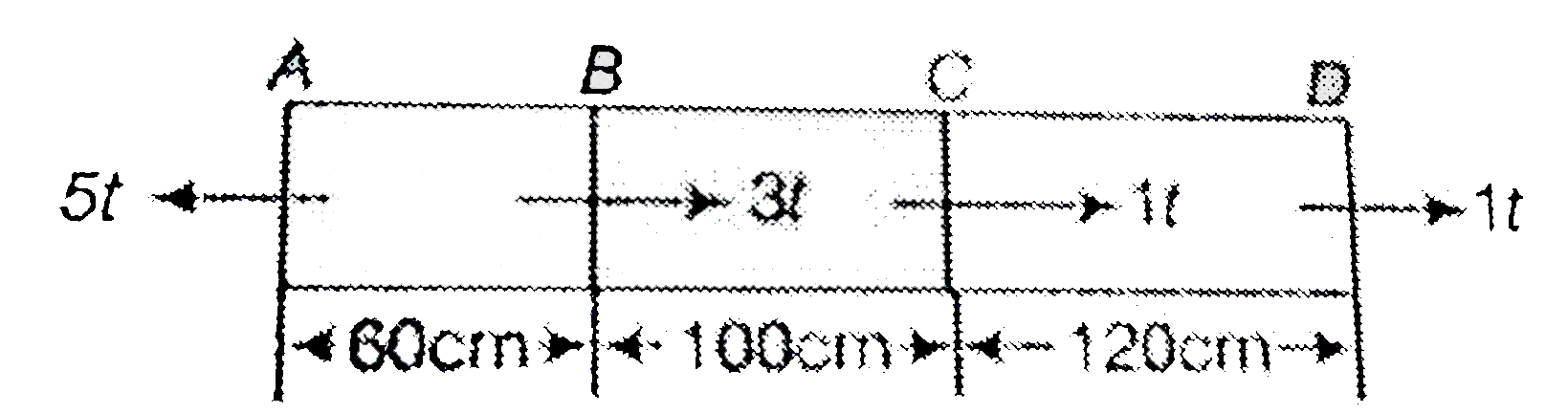
Find the total elongation of the bar, if the bar is subjected to axical froces as shown in figure . The cross-section area of bar is 10cm2 .
[TakeE=8×102dyne/cm2]
0.01 cm
0.5 cm
0.0675 cm
0.775 cm
The correct Answer is:C
Let δl= total enlogation of the bar, A = area,
E=8×102. Let make the free body diagram .

Using equation δl=1AE(F1l1+F2l2+F3l3)
δl=110×8×102(5×60+2×60+1×120)
δl=0.0675cm
Topper's Solved these Questions
Similar Questions
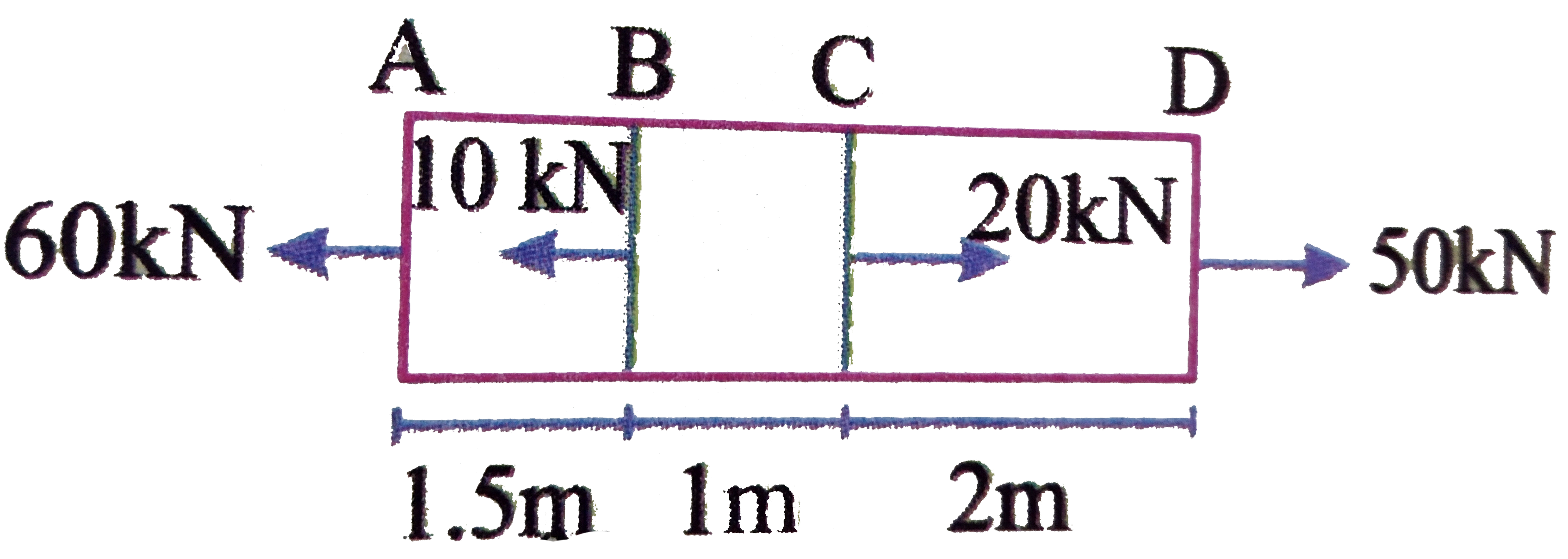
A steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
View SolutionA bar is subjected lu axial forces as shown. is the modulus of elasticity of the bar is E and A is it cross-section area. Its elongation will be

View Solution
Knowledge Check
To double the length of a iron wire having 0.5cm2 area of cross-section, the required force will be (Y=1012dyne/cm2)
A1.0×10−7NB1.0×107NC0.5×10−7ND0.5×1012 dyneThe magnetization of a bar magnet of length 5 cm,cross-sectional area 2cm2 and magnetic moment 1 Am2 is
A1×105AmB2×105AmC3×105AmD4×105AmIf a magnetising field of 1600A/m produces a magnetic flux of 14×10−5Wb in an iron bar of cross-sectional area 0.2cm2. Then,
Amagnetic permeability of iron rod is around 1000Bmagnetic susceptibility is very larger than unityCmagnetic susceptibility is 340DNone of the above
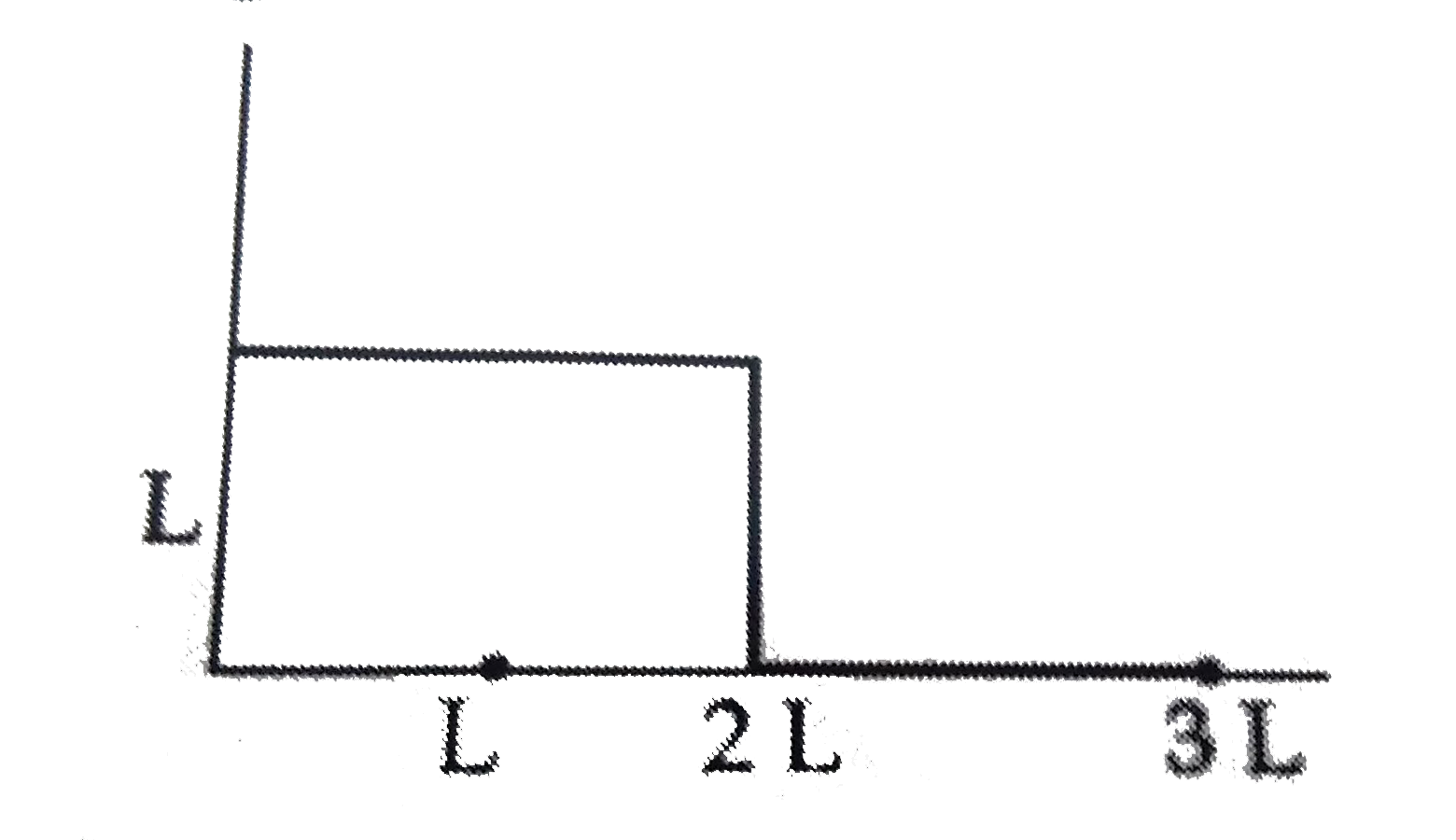
the position vector of the centre of mass lt
→
r cm of an asymmetric uniform bar of negligible area of cross - section as shown in figure is :
View SolutionTwo short bar moment each 200A−m2 are placed as shown in the figure at the corners of a square of side 10 cm.The magnetic induction at P is

View SolutionDetermine the elongation of the steel bar 1m long and 1.5cm2 cross-sectional area when subjected to a pull of 1.5×104N.
(TakeY=2.0×1011N/m2).
View SolutionTwo short bar magnets of moment each 100A−m2are placed as shown in figure at the corners of a square of side 10 cm.The magnetic induction at P is
View SolutionTwo bars are untressed and have lengths of 25cm and 30cm at 20∘C as shown in Figure. Bar(1) is of aluminium and bar (2) is of steel. The croos-sectional area of bars are 20cm2 for aluminium and 10cm2 for steel. Assuming that the top and bottom supports are rigid, stress in Nmm2 when the temperature is 700C. (Nearly)
(Ya=0.70×105N/mm2Ys=2.1×105N/mm2.αa=24×10−6/0C and αs=12.×10−6/0C)
_E01_126_Q01.png)
View Solution
