Determine the elongation of the steel bar 1m long and 1.5cm2 cross-sectional area when subjected to a pull of 1.5×104N.
(TakeY=2.0×1011N/m2).
The correct Answer is:A, D
To determine the elongation of the steel bar, we will use the formula for elongation (ΔL) given by:
ΔL=F⋅LA⋅Y
where:
- F = applied force (in Newtons)
- L = original length of the bar (in meters)
- A = cross-sectional area (in square meters)
- Y = Young's modulus (in Newtons per square meter)
1. Identify the given values:
- Length of the steel bar, L=1m
- Cross-sectional area, A=1.5cm2=1.5×10−4m2 (conversion from cm² to m²)
- Applied force, F=1.5×104N
- Young's modulus, Y=2.0×1011N/m2
2. Substitute the values into the elongation formula:
ΔL=F⋅LA⋅Y
ΔL=(1.5×104)⋅(1)(1.5×10−4)⋅(2.0×1011)
3. Calculate the denominator:
A⋅Y=(1.5×10−4)⋅(2.0×1011)=3.0×107N
4. Calculate the elongation:
ΔL=1.5×1043.0×107
ΔL=0.5×10−3m
5. Convert the elongation to millimeters:
ΔL=0.5mm
Final Answer:
The elongation of the steel bar is 0.5mm.
---
- F = applied force (in Newtons)
- L = original length of the bar (in meters)
- A = cross-sectional area (in square meters)
- Y = Young's modulus (in Newtons per square meter)
- Length of the steel bar, L=1m
- Cross-sectional area, A=1.5cm2=1.5×10−4m2 (conversion from cm² to m²)
- Applied force, F=1.5×104N
- Young's modulus, Y=2.0×1011N/m2
ΔL=F⋅LA⋅Y
ΔL=(1.5×104)⋅(1)(1.5×10−4)⋅(2.0×1011)
A⋅Y=(1.5×10−4)⋅(2.0×1011)=3.0×107N
ΔL=1.5×1043.0×107
ΔL=0.5×10−3m
ΔL=0.5mm
The elongation of the steel bar is 0.5mm.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.115videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.215videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective10videos
ELASTICITY
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions434videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
A steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
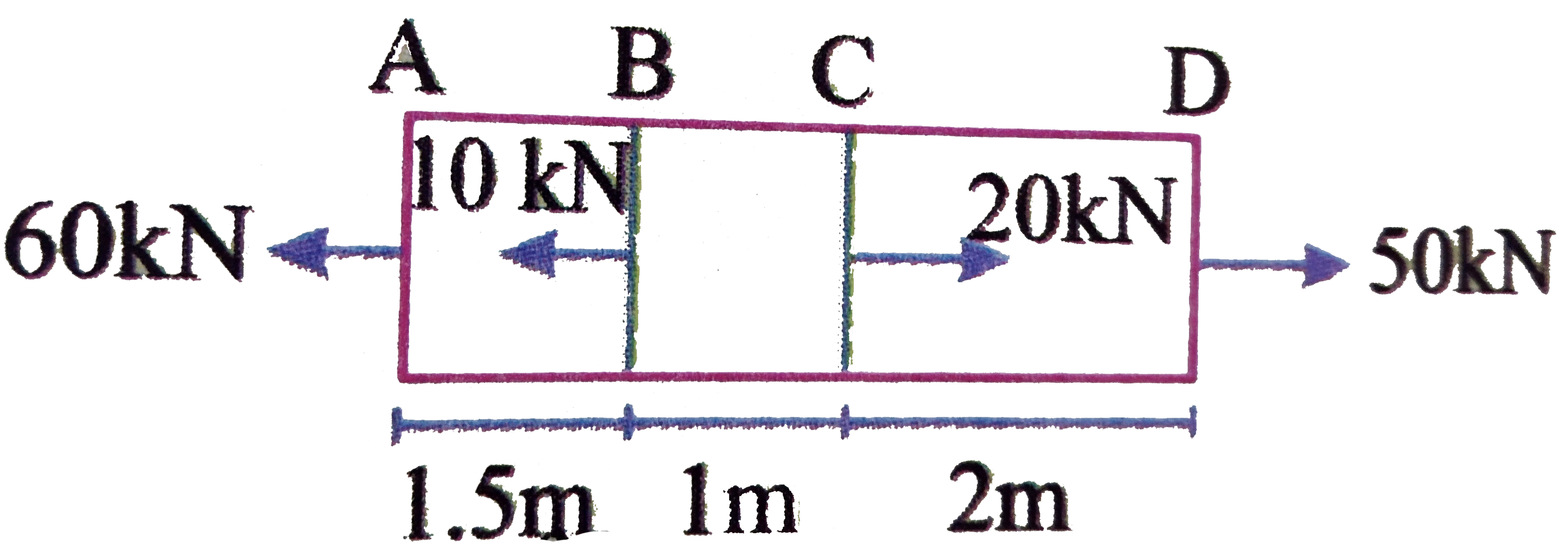 View Solution
View SolutionA copper rod with length 1.4 m and area of cross-section of 2cm2 is fastened to a steel rod with length L and cross-sectional area 1cm2. The compound rod is subjected to equal and opposite pulls to magnitude 6.00×104 N at its ends .
(a) Find the length L of the steel rod if the elongation of the two rods are equal .
(b) What is stress in each rod ?
(c ) What is the strain in each rod ? [Ysteel=2×1011Pa,YCu=1.1×1011Pa]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnitude of force developed by raising temperature from 0∘ to 100∘C of an iron bar 1.00 m long and 1cm2 cross-sectional area (α=10−5/.∘CandY=1011N/m2)
A103NB104NC105ND109N - Question 2 - Select One
A brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2A1.5mB1.8mC1mD2m - Question 3 - Select One
Find the total elongation of the bar, if the bar is subjected to axical froces as shown in figure . The cross-section area of bar is 10cm2 .
[TakeE=8×102dyne/cm2]
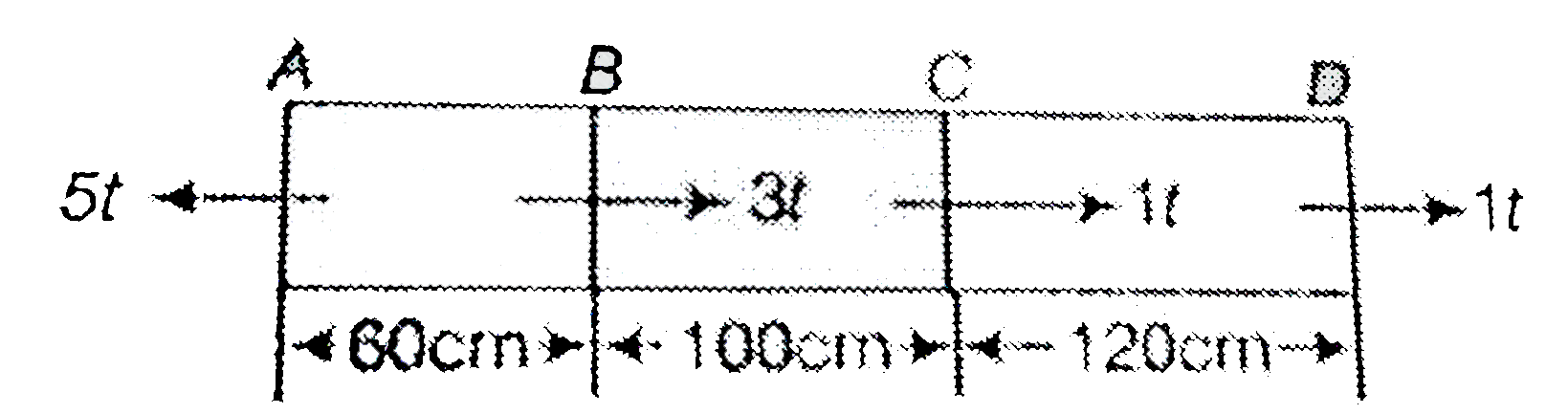 A0.01 cmB0.5 cmC0.0675 cmD0.775 cm
A0.01 cmB0.5 cmC0.0675 cmD0.775 cm
A uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View SolutionA brass rod of length 2 m and corss-sectinal area 2.0cm2 is attached to end to a steel rod of length L and corss-sectinal area 1.0cm2. The compound rod is subjected to equal and opposite pulls of magnitude 5×104N at its ends.
If the elongations of the two rods are equal, then the length of the steel rod L is (Ybrass=1.0×1011Nm−2 and ysteel=2.0×1011Nm−2)View SolutionWhat is the force requiredto stretch a steel wire of 1cm2 cross-section to 1.1 times its length ? (Y=2×1011N/m2)
View SolutionTwo exactly similar wire of steel and copper are stretched by equal force. If the difference in their elongations is 0.5 cm, the elongation (l) of each wire is
Ys(steel)=2.0×1011N/m2
Yc(copper)=1.2×1011N/m2View SolutionA 1 m long steel wire of cross-sectional area 1mm2 is extended 1 mm. If Y=2×1011Nm−2, then the work done is
View Solution

