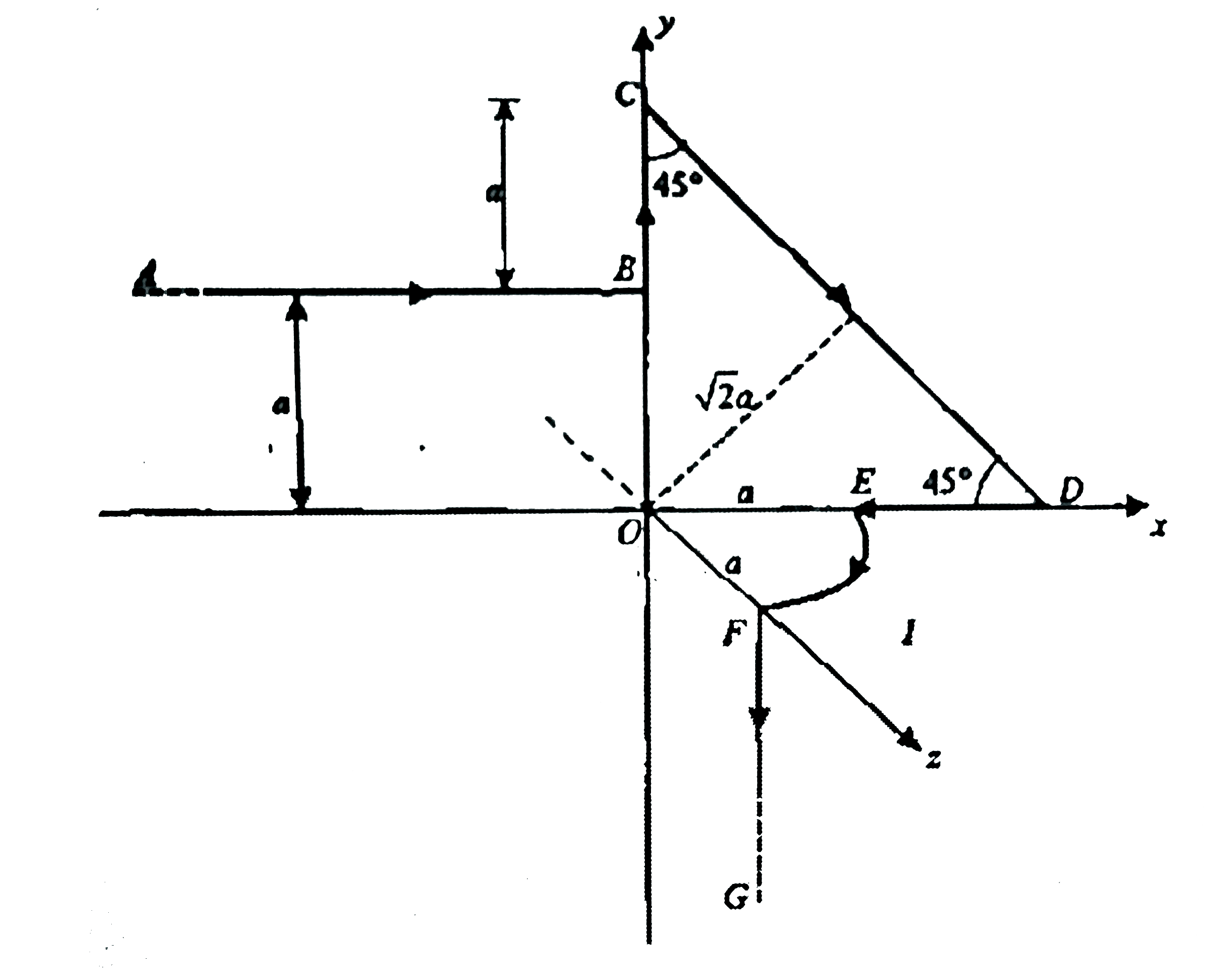
Find →B at the origin due to the long wire carrying current I.

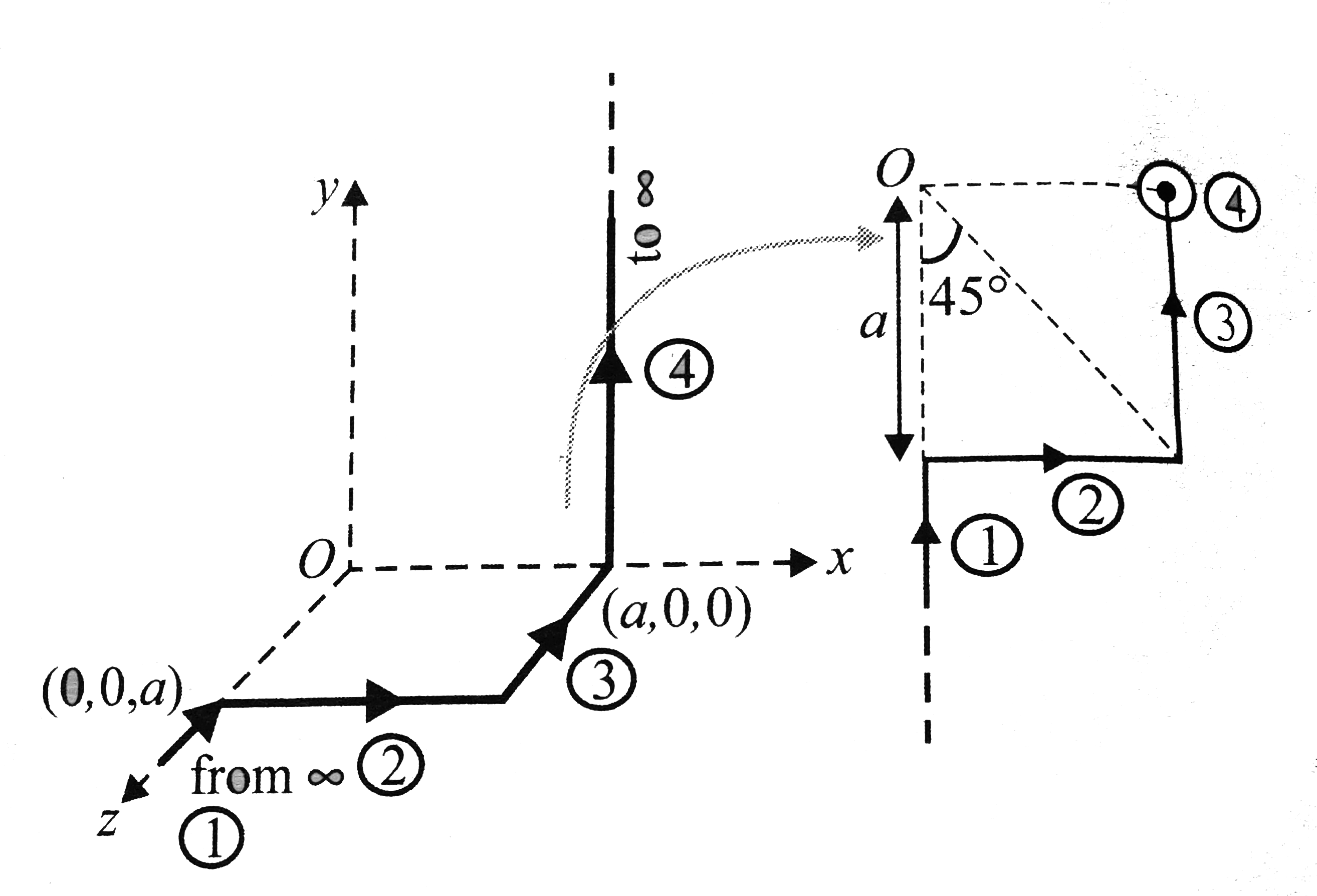
Net magnetic field at origin is the vector sum of magnetic fields
due to wires (1) ,(2),(3), and (4).
→B=→B1+→B2+→B3+→B4
where B1=0, as direction of current wire passes through origin.
Magnetic field due to wire (2),
→B2=μ04πIA[sin0∘+sin45∘]ˆj
Magnetic field due to wire (2) and wire (3) is equal to →B2=→B3
⇒→B2=→B3=μ0I4√2πaˆj
Magnetic field due to wire (4),
→B4=μ04πIa[sin0∘+sin90∘]ˆk=μ0I4πaˆk
So, →B=2→B2+→B4=μ0I4πa[√2ˆj+ˆk]
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Find the magnitude of the magnetic field at the origin O due to very long conductor carrying current I of the shape as shown in figure.
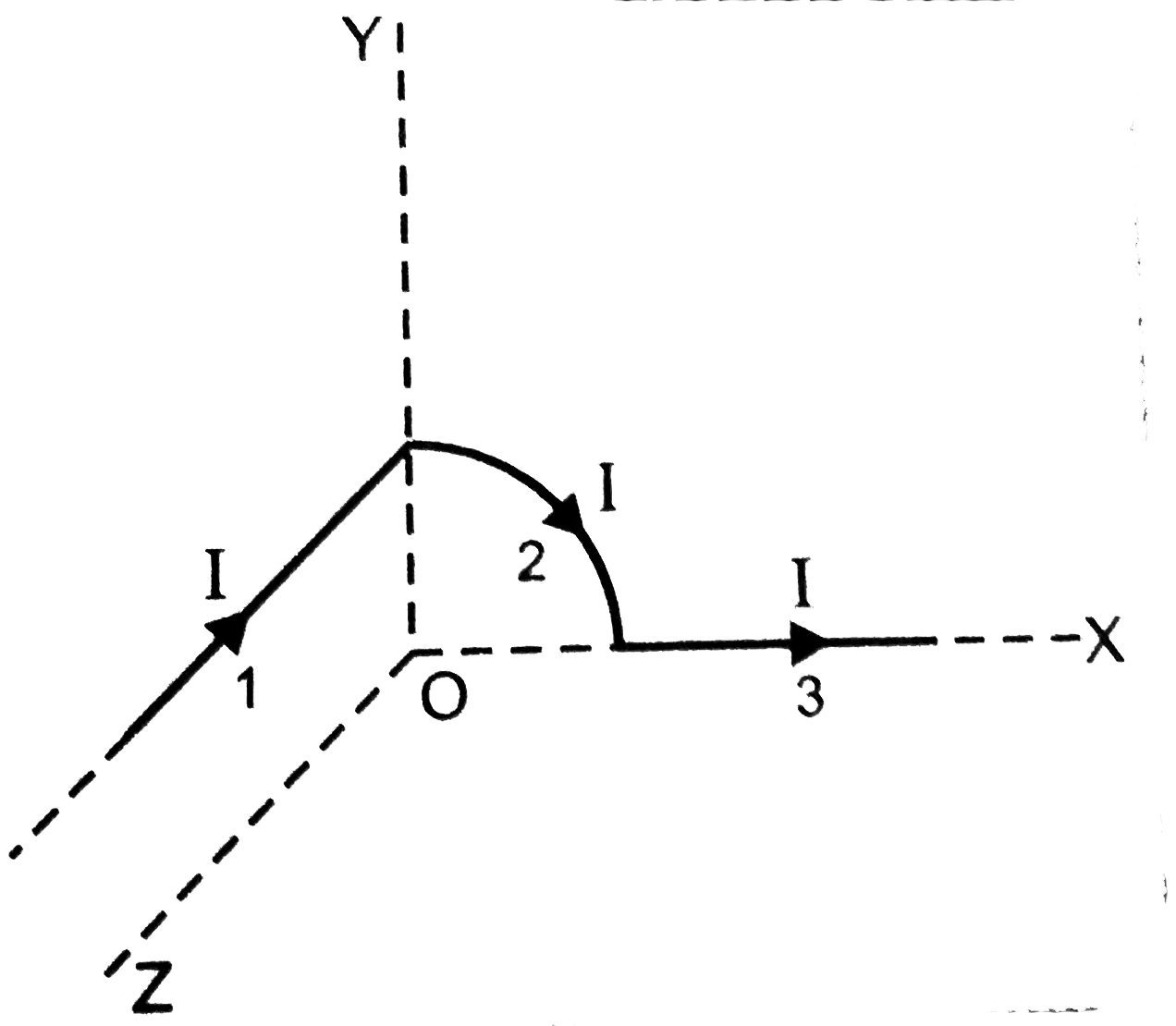 View Solution
View SolutionFind the magnetic induction at the point O if the wire carrying a current I=8.0A has the shwon in Fig.


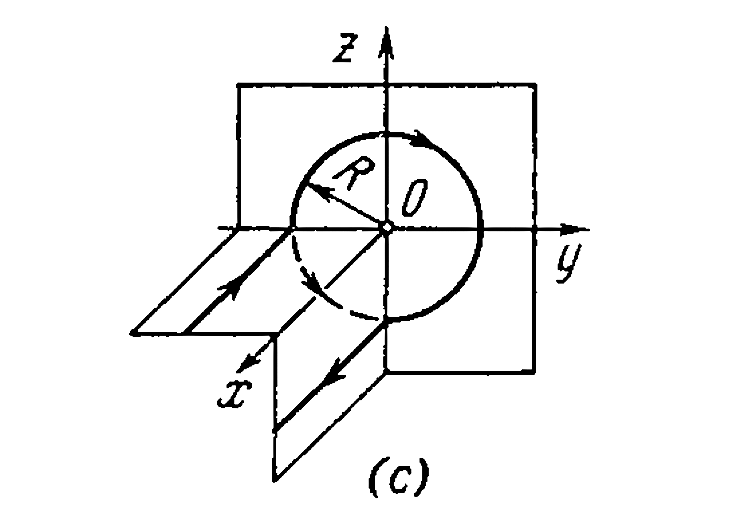
The radius of the curved part of the wire is R=100mm, the linear parts of the wire are very long.View Solution
Knowledge Check
- Question 1 - Select One
The direction of magnetic field at a point due to an infinitely long wire carrying current is
Aparallel to the currentBantiparallel to the currentCalong the perpendicular drawn from a point on the wireDperpendicular to the plane containing the conductor and the point - Question 2 - Select One
The magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distance
A rod CD of length b carrying a current I2 is placed in a magentic field due to a thin long wire AB carrying current I1 as shown in figure. Then find the net force experience by the wire
View SolutionFind the field at the origin O due to the current i=2A.
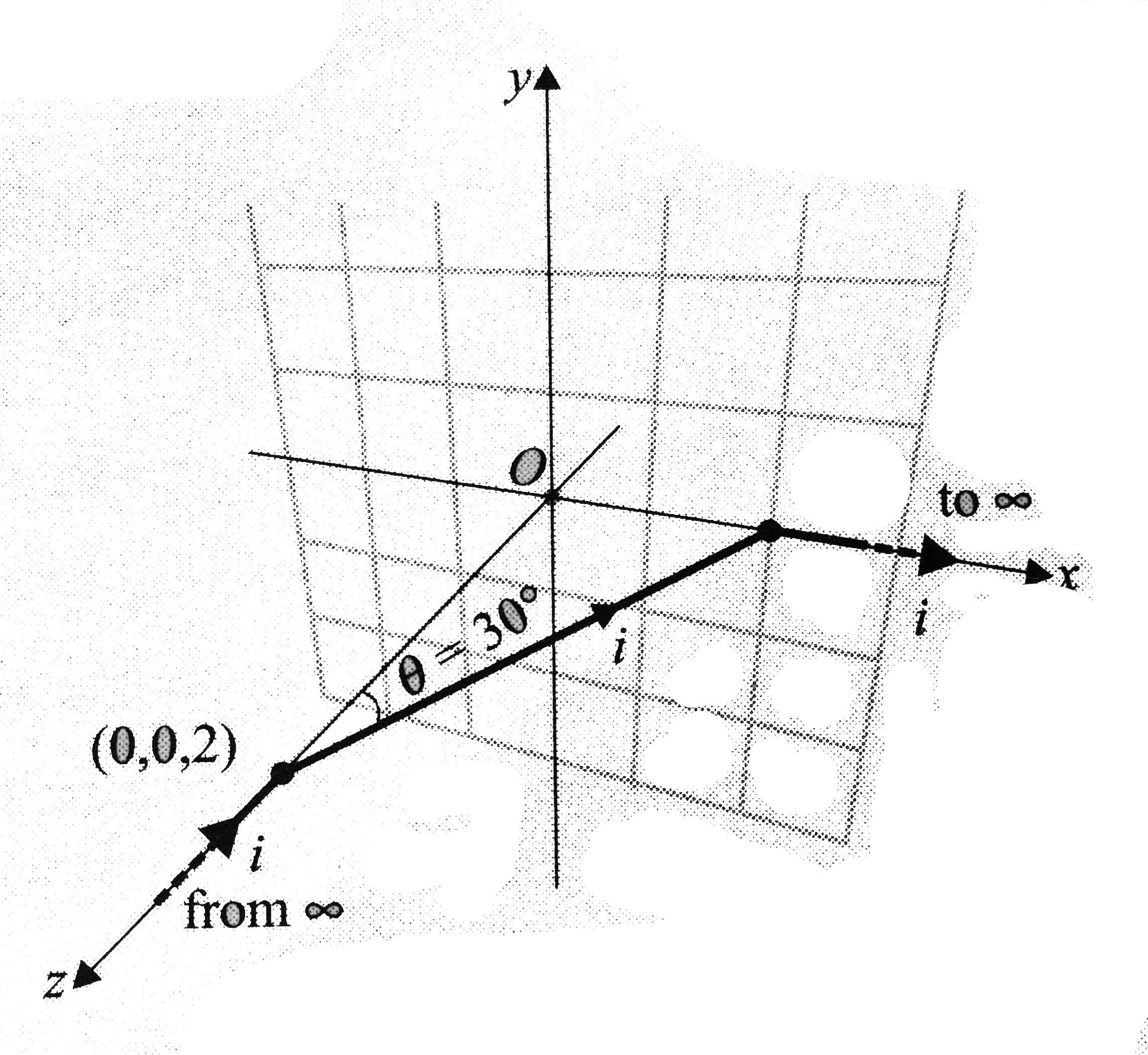 View Solution
View SolutionFind the magnetic induction vector at origin O due to the current carrying wire configuration as shown in figure-4.33.
 View Solution
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
 View Solution
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.
 View Solution
View Solution

