For a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
(2Dλ)a
Dλa
Daλ
2Daλ
The correct Answer is:A
For the condition of maxima sinθ=λa
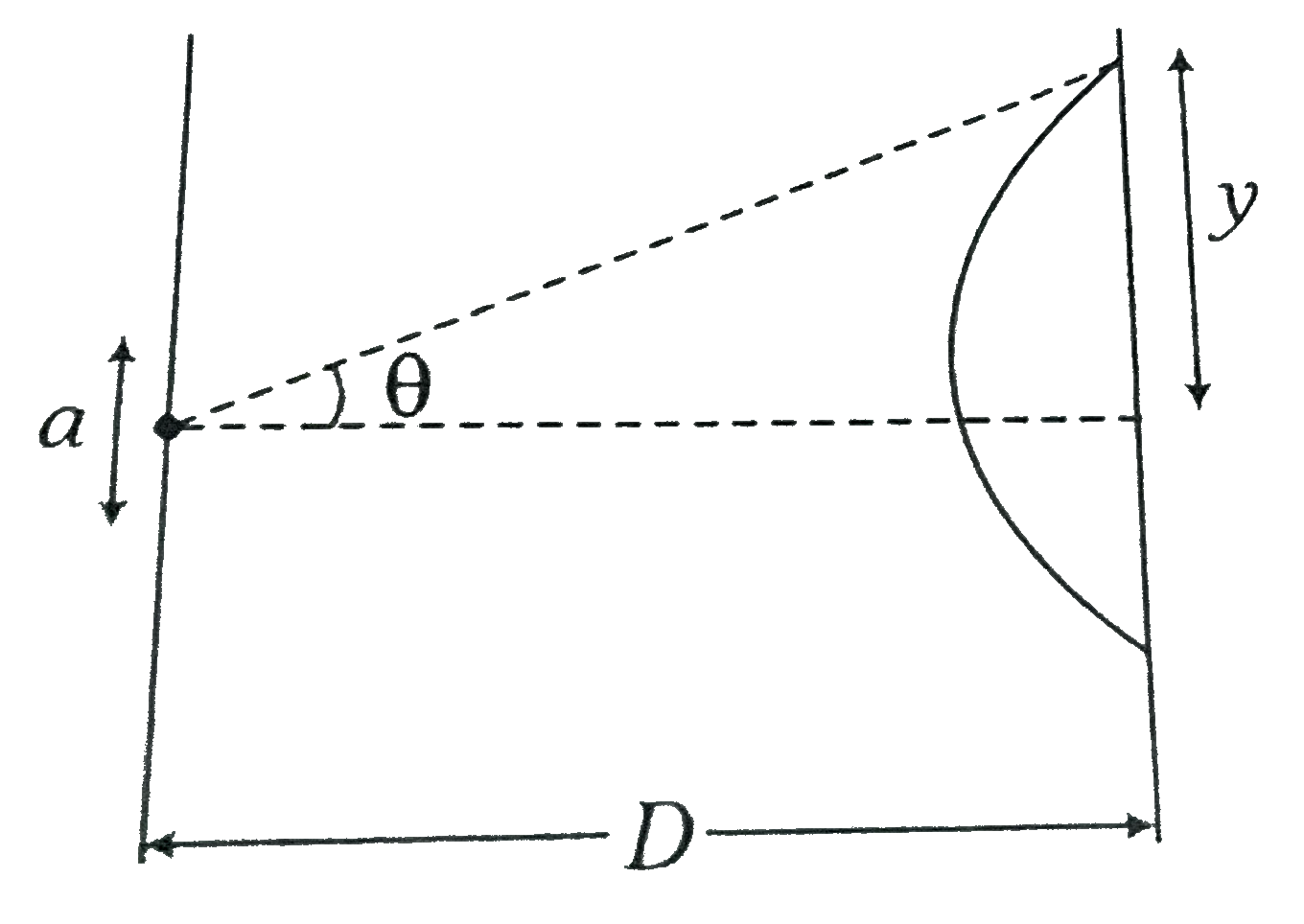
From the geometry
sinθ=θ=yD
So, yD=λa⇒y=λDa
Hence, width of central maxima =2y=2λDa
Topper's Solved these Questions
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE main (Only one option is Correct )
22 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced Only one option is correct
23 Videos
- WAVE OPTICSBOOK - DC PANDEYCHAPTER - WAVE OPTICSEXERCISE - match column
4 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEYCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER
22 Videos
Similar Questions
A parallel beam of light of wavelength 6000Å gets diffracted by a single slit of width 0.3 mm. The angular position of the first minima of diffracted light is :
View SolutionA single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View Solution
Knowledge Check
For a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
ADλaBDa/λC12D/aD2DλaFor a parallel beam of monochromatic light of wavelength 'λ' differaction is produced by a single slit whose width 'a' is of the order as wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
ADλaBDλaC2DaλD2DλaA monochromatic light of wavelength λ falls on a single slit. The first secondary maximum occurs at 30∘ if the width of the slit is equal to
Aλ2B3λ2CλD2λ.
A single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View SolutionA single slit of width 0.20mm is illuminated with light of wavelength 500nm. The observing screen is placed 80cm from the slit. The width of the central bright fringe will be
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View SolutionLight of wavelength λ is incident on a single sht of width. 'a' and the distance between slit and screen is 'D. In diffraction pattern, if slit width is equal to the width of the central maximum then 'O is equal to
View SolutionLight of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
View Solution
