For an LCR circuit driven at frequency ω, the equation reads Ldidt+Ri+qC=υi=υmsinωt
(i) Multiply the equation by I and simplify where possible. (ii) Interpret each term physically.
(iii) Cast the equation in the form of a conservation of energy statement.
(iv) Intergrate the equation over one cycle to find that the phase difference between υ and i must be acute.
For an LCR circuit driven at frequency ω, the given eqn. is
Ldidt+Ri+qC=υ1=υmsinωt
Multiplying both sides by I, we get Lididt+Ri2+qiC=υi
Now, LIdidt=ddt(12Li2)= rate of change of energy stored in inductor, R2i = rate of Joule heating loss
qCi=ddt(q22C) = rate of change of energy stroe in capacitor
υ×i = rate at which driving force pours in energy Hence, eqn. (ii) is in the form of convervation of energy statement.
Integrating both sides of (ii) w.r.t. t over one full cycle (0→T), we may write
∫T0ddt(12Li2+q22C)dt+∫T0Ri2dt=∫T0υidt
zero + positive = ∫T0υ i dt
∴∫T0υidt>0, which is possible only when phase diff. between υ and i is an acute angle.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)A6 unitsB5 unitsC1 unitsD7 units - Question 2 - Select One
If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
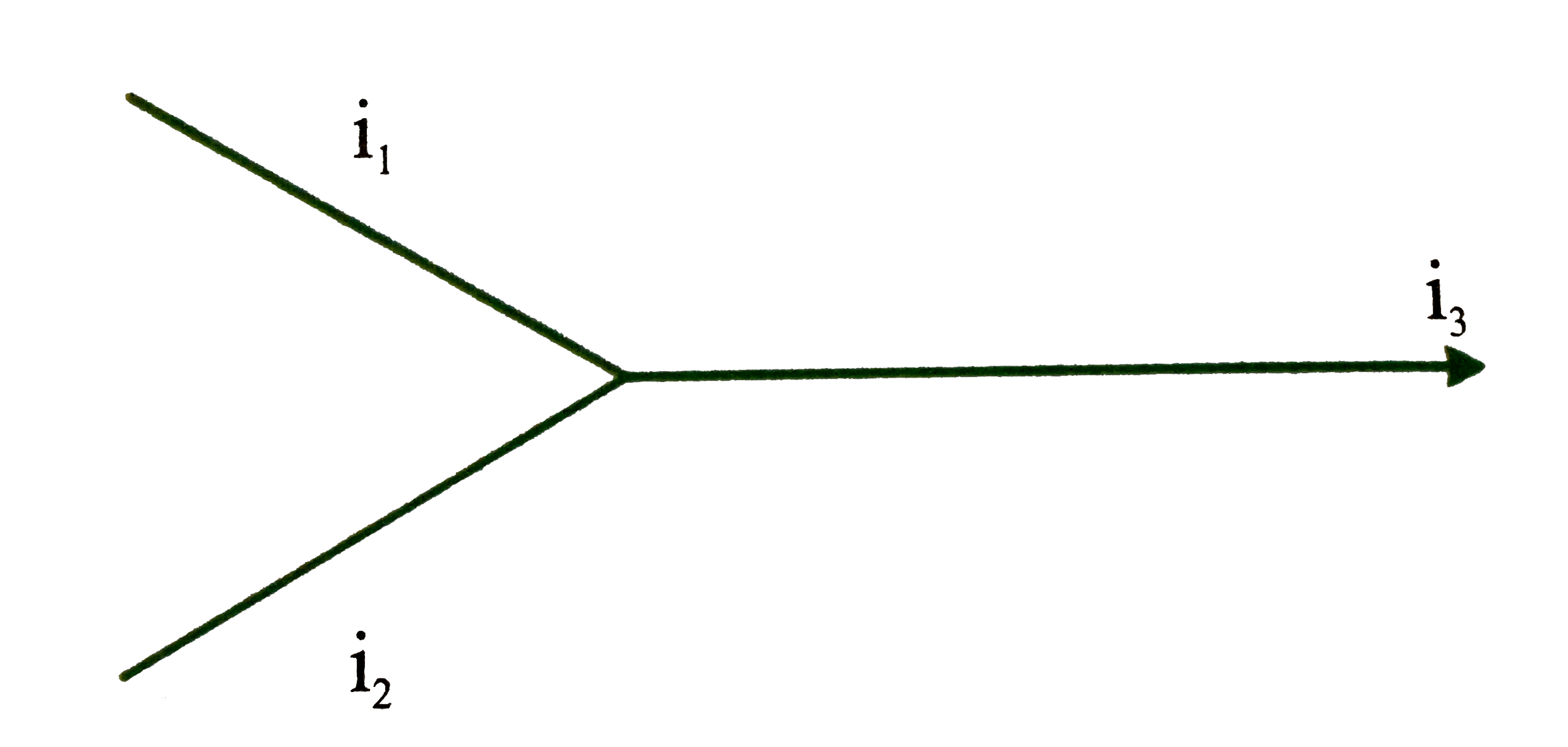 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ] - Question 3 - Select One
The displacement of a particle is represented by the equation y=sin2ωt the motion is
Anon - periodicBperiodic but not simple harmonicCsimple harmonic with period 2π/ωDsimple harmonic with period π/ω
The equation of an alternating current is I=20sin300 pi t .Calculate the frequency and r.m.s value of current
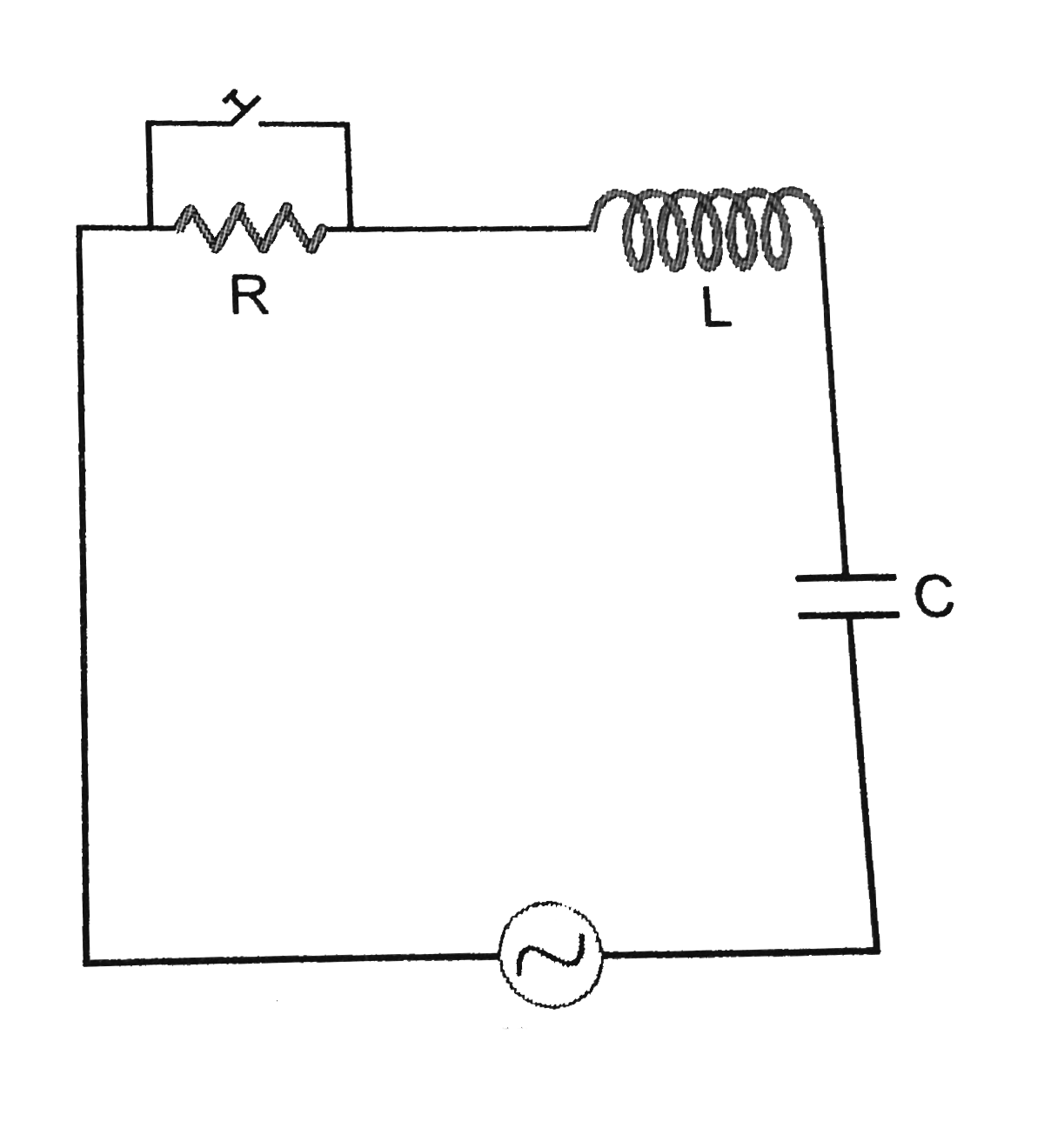
View SolutionIn the LCR circuit shown in Fig., the ac driving voltage is υ=υmsinωt.
(i) Write down the equation of motion for q (t).
(ii) At t=t0, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.
 View Solution
View SolutionIn terms of q, the voltage equation for series L-C-R circuit is given by
View SolutionFor an ac circuit V=15sinωt and I=20cosωt the average power consumed in this circuit is
View Solutiony=Acosωt+Bsinωt is a solution of the differential equation
View Solution

