For capacitors in series combination, total capacitance C is given by
1C=1C1+1C2+....
C=C1+C2+....
C=C1C2+C2C3+ . . . .
C+1C1+C2+.....
The correct Answer is:A
To find the total capacitance C for capacitors in series, we can follow these steps:
1. Understanding the Configuration:
When capacitors are connected in series, they are connected end to end, and the same charge q flows through each capacitor. This means that the charge on each capacitor is the same.
2. Identifying the Potential Differences:
Let’s denote the capacitances of the capacitors as C1,C2, and C3. The potential differences across these capacitors will be V1,V2, and V3 respectively. The total potential difference V across the series combination is given by:
V=V1+V2+V3
3. Using the Definition of Capacitance:
The capacitance C of a capacitor is defined as:
C=qV
Therefore, for each capacitor, we can write:
V1=qC1,V2=qC2,V3=qC3
4. Substituting the Values:
Substituting these values into the total potential difference equation gives:
V=qC1+qC2+qC3
5. Factoring Out the Charge:
Since q is common in all terms, we can factor it out:
V=q(1C1+1C2+1C3)
6. Expressing Total Capacitance:
From the definition of capacitance, we can express the total capacitance Ceq for the series combination as:
Ceq=qV
Substituting for V gives:
Ceq=qq(1C1+1C2+1C3)=1(1C1+1C2+1C3)
7. Final Expression:
Therefore, the total capacitance Ceq for capacitors in series is given by:
1Ceq=1C1+1C2+1C3
When capacitors are connected in series, they are connected end to end, and the same charge q flows through each capacitor. This means that the charge on each capacitor is the same.
Let’s denote the capacitances of the capacitors as C1,C2, and C3. The potential differences across these capacitors will be V1,V2, and V3 respectively. The total potential difference V across the series combination is given by:
V=V1+V2+V3
The capacitance C of a capacitor is defined as:
C=qV
Therefore, for each capacitor, we can write:
V1=qC1,V2=qC2,V3=qC3
Substituting these values into the total potential difference equation gives:
V=qC1+qC2+qC3
Since q is common in all terms, we can factor it out:
V=q(1C1+1C2+1C3)
From the definition of capacitance, we can express the total capacitance Ceq for the series combination as:
Ceq=qV
Substituting for V gives:
Ceq=qq(1C1+1C2+1C3)=1(1C1+1C2+1C3)
Therefore, the total capacitance Ceq for capacitors in series is given by:
1Ceq=1C1+1C2+1C3
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MBD -HARYANA BOARDCHAPTER - ELECTROSTATICSEXERCISE - LONG ANSWER TYPE QUESTIONS
14 Videos
- Electromagnetic WavesBOOK - MBD -HARYANA BOARDCHAPTER - Electromagnetic WavesEXERCISE - Example
7 Videos
- MAGNETISMBOOK - MBD -HARYANA BOARDCHAPTER - MAGNETISMEXERCISE - OBJECTIVE TYPE QUESTIONS
17 Videos
Similar Questions
Derive expresion for capacitance of a parallel plate capacitor and explain the combination of capacitors in series.
Or.
Write expression for three capacitors in series and parallel combinations.
View SolutionIf the total capacitance of the combination of identical capacitors shown in figure between A and B is given by nC then find n.
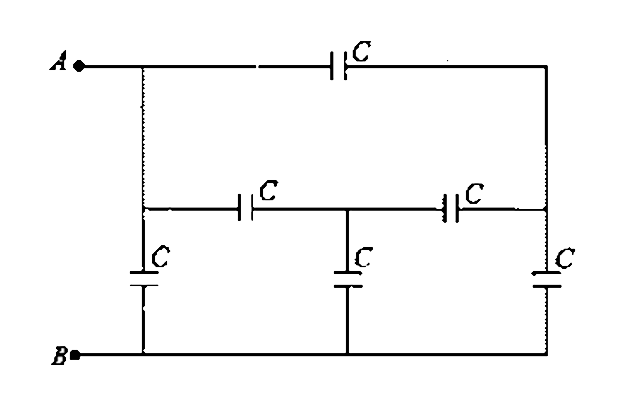
View Solution
Knowledge Check
Two capacitors of capacity C1andC2 are connected in series. The combined capacity C is given by
AC1+C2BC1−C2CC1C2(C1+C2)D(C1+C2)C1C2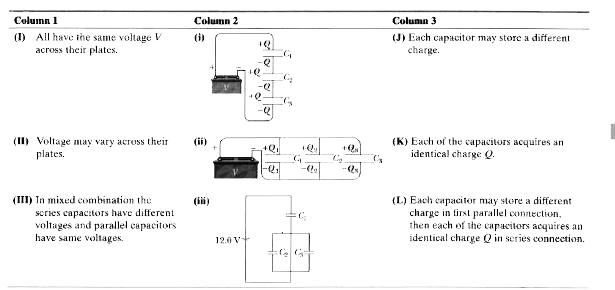
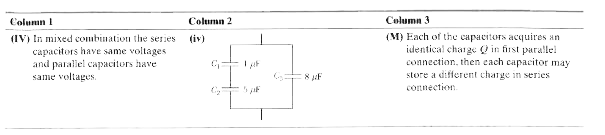 What are the conditions when capacitors is in mixed combination, that is parallel and series combination respectively?A(III) (IV) (K)B(IV) (I) (M)C(III) (III) (L)D(I) (I) (M)
What are the conditions when capacitors is in mixed combination, that is parallel and series combination respectively?A(III) (IV) (K)B(IV) (I) (M)C(III) (III) (L)D(I) (I) (M)A capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by
 AC0(V0−V)V0BC0(V−V0)V0CC0(V+V0)VDC0(V0−V)V
AC0(V0−V)V0BC0(V−V0)V0CC0(V+V0)VDC0(V0−V)V
Total energy stored in series or parallel combination of capacitor is equal to ………. stored in ………...
View SolutionThree capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination ?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply ?
View SolutionIn a series combination of two capacitances C and C (Cgt C) (as shown in the circuit),
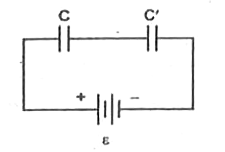
View SolutionWhen two capacitors are connected in series, the equivalent capacitance is 1.2μF. When they are connected in parallel, the equivalent capacitance is 5μF. The capacitances of the capacitors are
View SolutionIf there are n capacitors each of capacitance C in series combination connected to a V volt source, then the energy stored in each capacitor is equal to :
View Solution
