For photoelectric effect with incident photon wavelength λ, the stopping potential is V0 Select the correct graph.


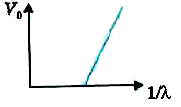

The correct Answer is:A, C
To solve the problem regarding the photoelectric effect and the stopping potential V0 as a function of the incident photon wavelength λ, we can follow these steps:
1. Understand the Photoelectric Effect:
The photoelectric effect occurs when light (photons) hits a material and causes the emission of electrons. The energy of the incident photons is given by the equation:
E=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
2. Energy Considerations:
For an electron to be emitted, the energy of the photon must be greater than the work function ϕ of the material. The kinetic energy K of the emitted electrons can be expressed as:
K=E−ϕ=hcλ−ϕ
3. Relate Kinetic Energy to Stopping Potential:
The kinetic energy of the emitted electrons can also be related to the stopping potential V0 by the equation:
K=eV0
where e is the charge of the electron. Therefore, we can equate the two expressions for kinetic energy:
eV0=hcλ−ϕ
4. Rearranging the Equation:
Rearranging the equation gives us:
V0=hce⋅1λ−ϕe
This equation is in the form of a linear equation y=mx−c, where:
- y=V0
- x=1λ
- m=hce (slope)
- c=ϕe (y-intercept)
5. Graph Interpretation:
From the equation V0=hce⋅1λ−ϕe, we can see that the graph of V0 versus 1λ will be a straight line with a positive slope. The x-intercept occurs when V0=0, which gives us the threshold wavelength where photoemission starts.
6. Select the Correct Graph:
Based on the linear relationship derived, we can identify that the correct graph will show a straight line with V0 on the y-axis and 1λ on the x-axis. The line will intersect the x-axis at the point corresponding to the threshold wavelength.
Final Answer:
The correct graph is the one that depicts a straight line with V0 on the y-axis and 1λ on the x-axis, indicating a linear relationship.
The photoelectric effect occurs when light (photons) hits a material and causes the emission of electrons. The energy of the incident photons is given by the equation:
E=hcλ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the incident light.
For an electron to be emitted, the energy of the photon must be greater than the work function ϕ of the material. The kinetic energy K of the emitted electrons can be expressed as:
K=E−ϕ=hcλ−ϕ
The kinetic energy of the emitted electrons can also be related to the stopping potential V0 by the equation:
K=eV0
where e is the charge of the electron. Therefore, we can equate the two expressions for kinetic energy:
eV0=hcλ−ϕ
Rearranging the equation gives us:
V0=hce⋅1λ−ϕe
This equation is in the form of a linear equation y=mx−c, where:
- y=V0
- x=1λ
- m=hce (slope)
- c=ϕe (y-intercept)
From the equation V0=hce⋅1λ−ϕe, we can see that the graph of V0 versus 1λ will be a straight line with a positive slope. The x-intercept occurs when V0=0, which gives us the threshold wavelength where photoemission starts.
Based on the linear relationship derived, we can identify that the correct graph will show a straight line with V0 on the y-axis and 1λ on the x-axis. The line will intersect the x-axis at the point corresponding to the threshold wavelength.
The correct graph is the one that depicts a straight line with V0 on the y-axis and 1λ on the x-axis, indicating a linear relationship.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( D - Multiple Choice Questions) )5videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS))11videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (JEE (Advanced) for IIT Entrance))15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test15videos
CURRENT ELECTRICITY
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
For photo - electric effect with incident photo wavelength λ the stopping is V0 identify the correct variation(s) of V0 with λand1/λ
A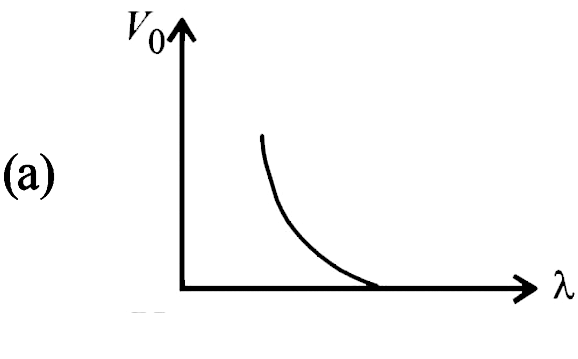 B
B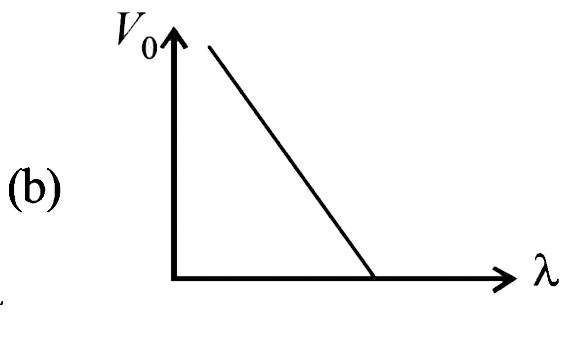 C
C D
D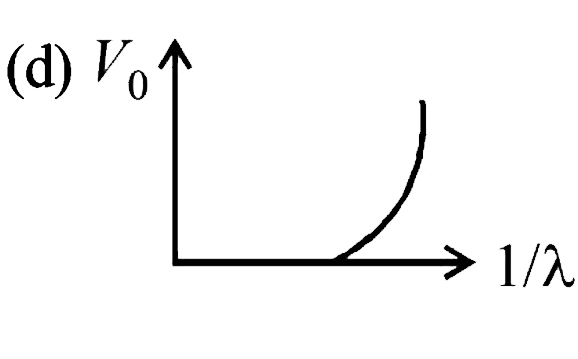
- Question 2 - Select One
When a photosensitive surface is illuminated with light of wavelength λ, the stopping potential is V0. But when light of wavelength 2λ is incident on the same surface, the stopping potential is V04. What is the threshold wavelength for the surface ?
A2λB3λC4λD5λ - Question 3 - Select One
In an experiment on photoelectric effect the frequency f of the incident light is plotted against the stopping potential V0. The work function of the metal is given by ( e is the electronic charge)
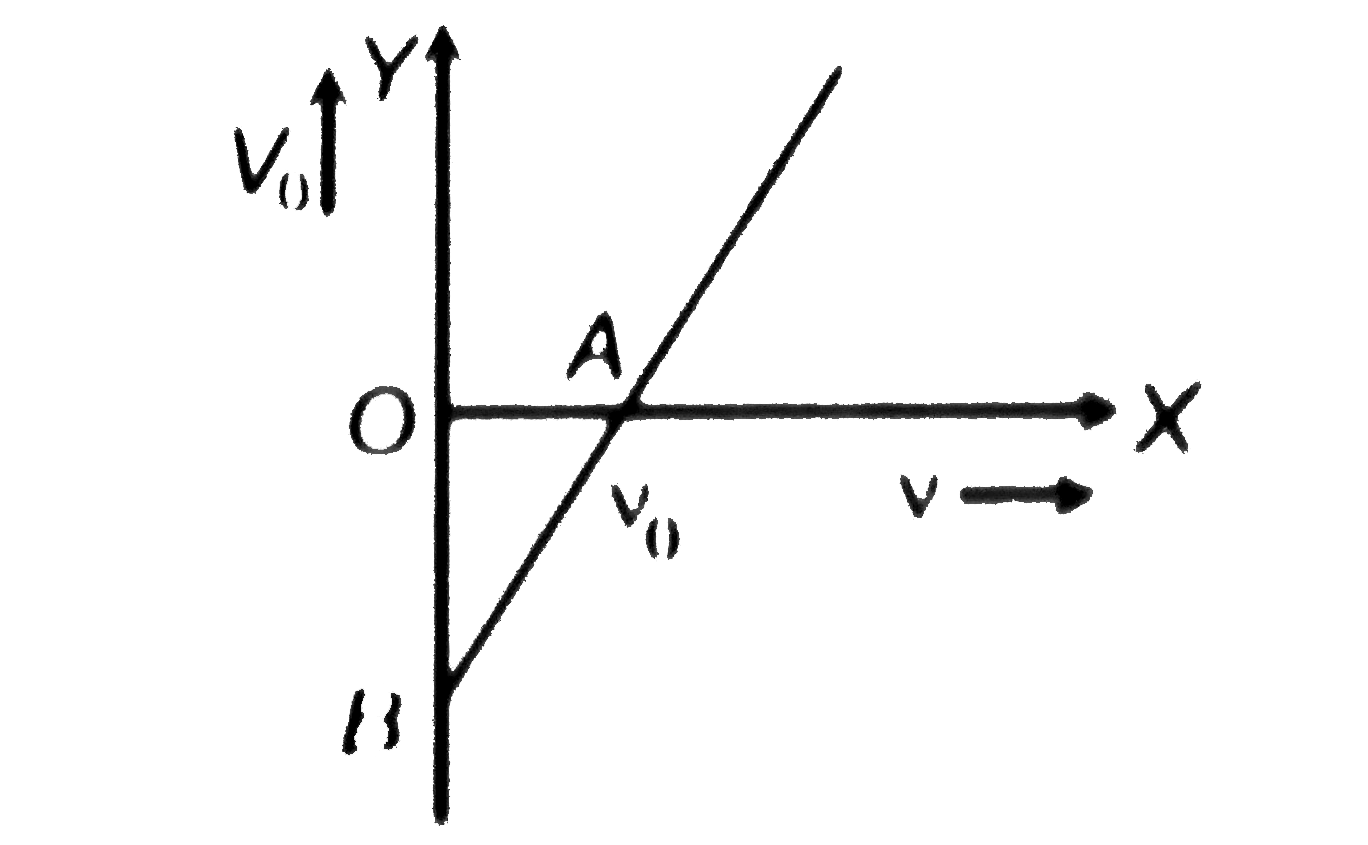 AOB×e in eVBOB in VoltCOA in VoltDThe slope of the line AB
AOB×e in eVBOB in VoltCOA in VoltDThe slope of the line AB
In photoelectric effect, stopping potential depends on
View SolutionWhen a centimeter thick surface is illuminated with light of wavelength λ, the stopping potential is V. When the same surface is illuminated by light of wavelength 2λ, the stopping potential is V3. Threshold wavelength for the metallic surface is
View SolutionWhen a certain metallic surface is illuminated with monochromatic light of wavelength λ, the stopping potential for photoelectric current is 3V0 and when the same surface is illuminated with light of wavelength 2λ, the stopping potential is V0. The threshold wavelength of this surface for photoelectrice effect is
View SolutionWhen a metallic surface is illuminated with radiation of wavelength λ , the stopping potential is V . If the same surface is illuminated with radiation of wavelength 2λ , the stopping potential is V4 . The threshold wavelength for the metallic surface is
View SolutionWhen a metallic surface of threshold wavelength 4λ is illuminated with light of wavelength λ the stopping potential is V. When the same surface is illuminated by the light of wavelength 2λ Stopping potential is V3 Threshold wavelength for the metallic surface is
View Solution

