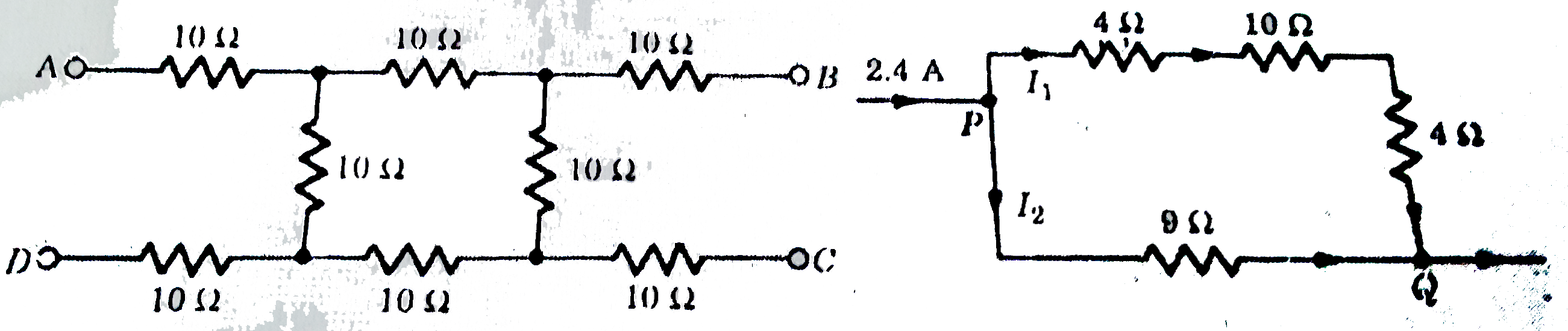For the combination of resistors shown in (fig.)
(a) find the equivalent resistance between
(i) C and D and
(ii) A and B.
 .
.
Video Solution
Text Solution
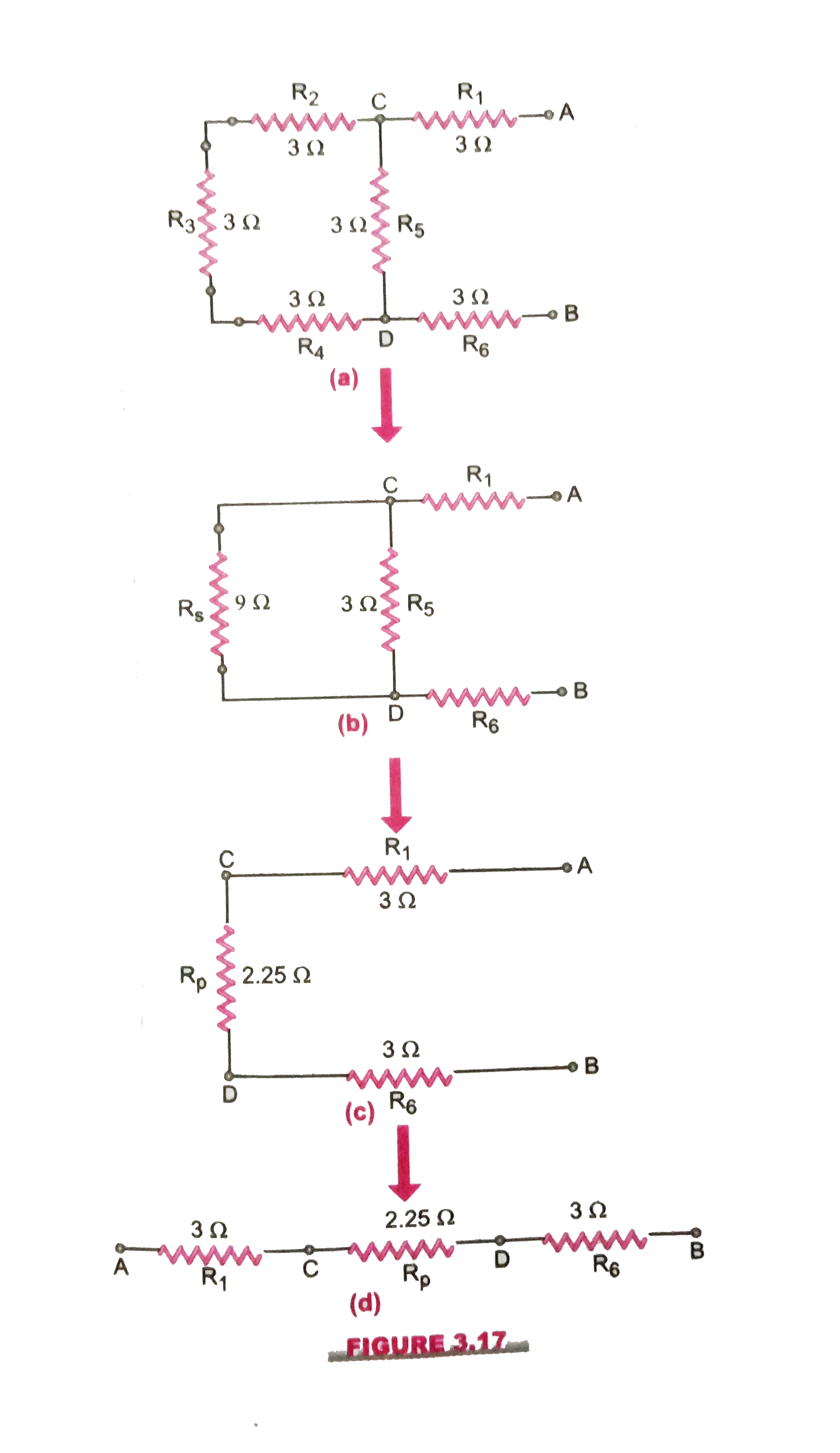
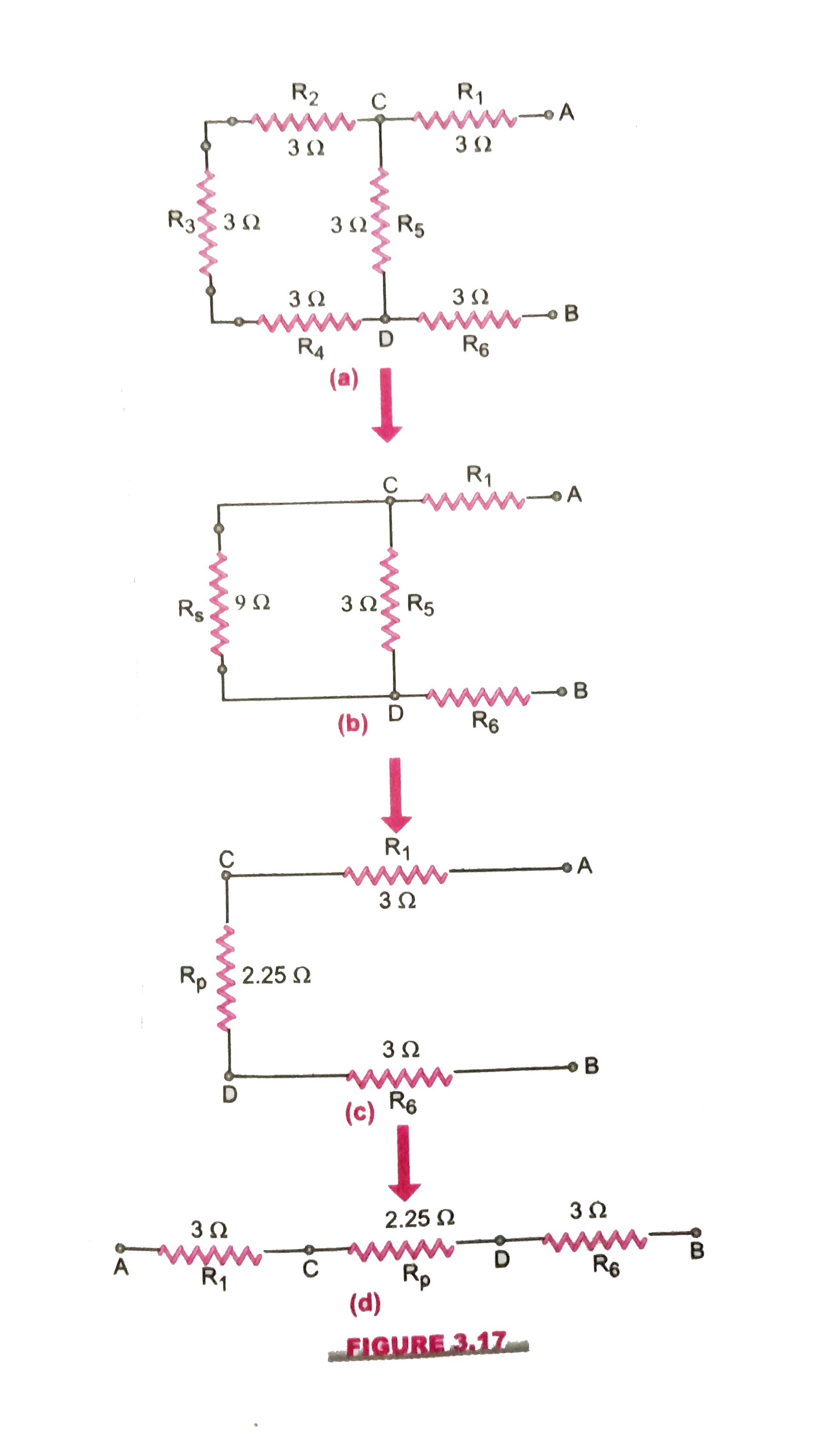
(i) The resistors R2,R3andR4 are in series. Their equivalent resistance Rs is given by
Rs=3Ω+3Ω+3Ω
=9Ω
Further, Rs(=9Ω)andR5(=3Ω) are in parallel, (Fig. 3.17) (b) and their equivalent resistance is given by
Rp=product of two resistancessum of two resistances
=9×39+3ω=2712Ω=2.25Ω
Thus, the equivalent resistance between C and D is 2.25Ω.
(ii) Now R1(=3Ω),Rp(=2.25Ω)
and R6(=3Ω)
are in series, (Fig. 3.17).
Thus,equivalent resistance between A and B, (Fig. 3.17)(d),
=R1+Rp+R6
=3Ω+2.25Ω+3Ω
=8.25Ω
 .
.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find equivalent resistance between A and D
 A2ΩB3ΩC1ΩD5Ω
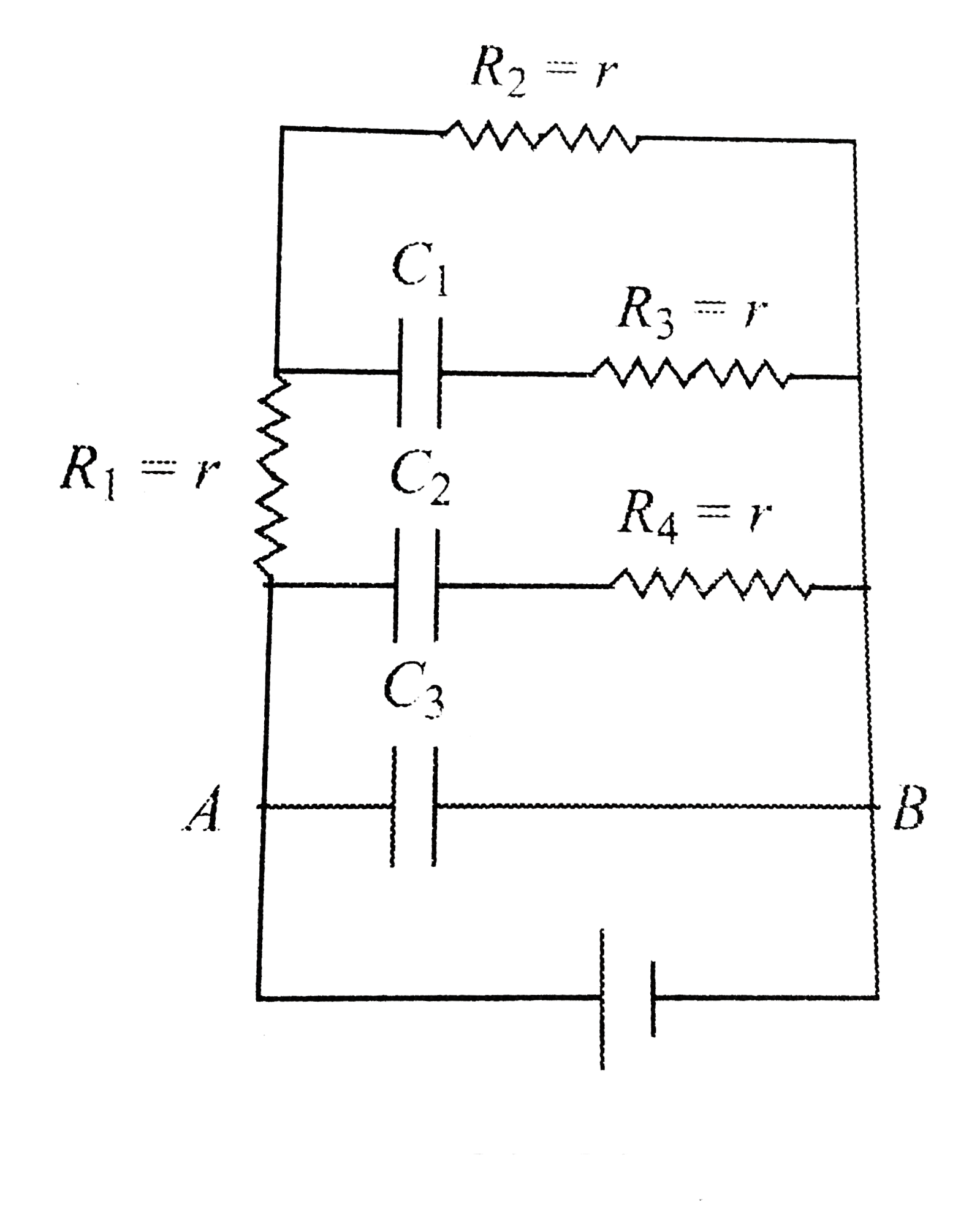
A2ΩB3ΩC1ΩD5ΩEquivalent resistance between A and B in Fig. is
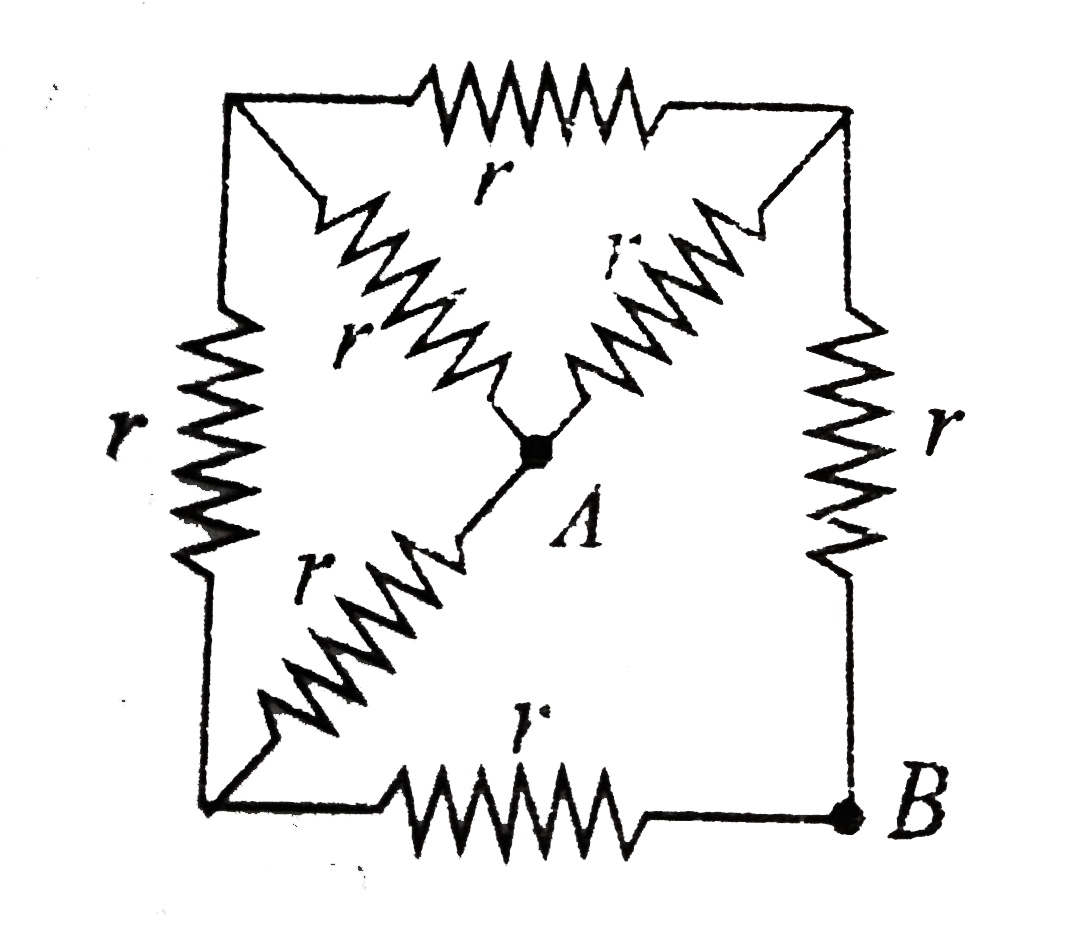 A8r/7B7r/8C3r/4Dr
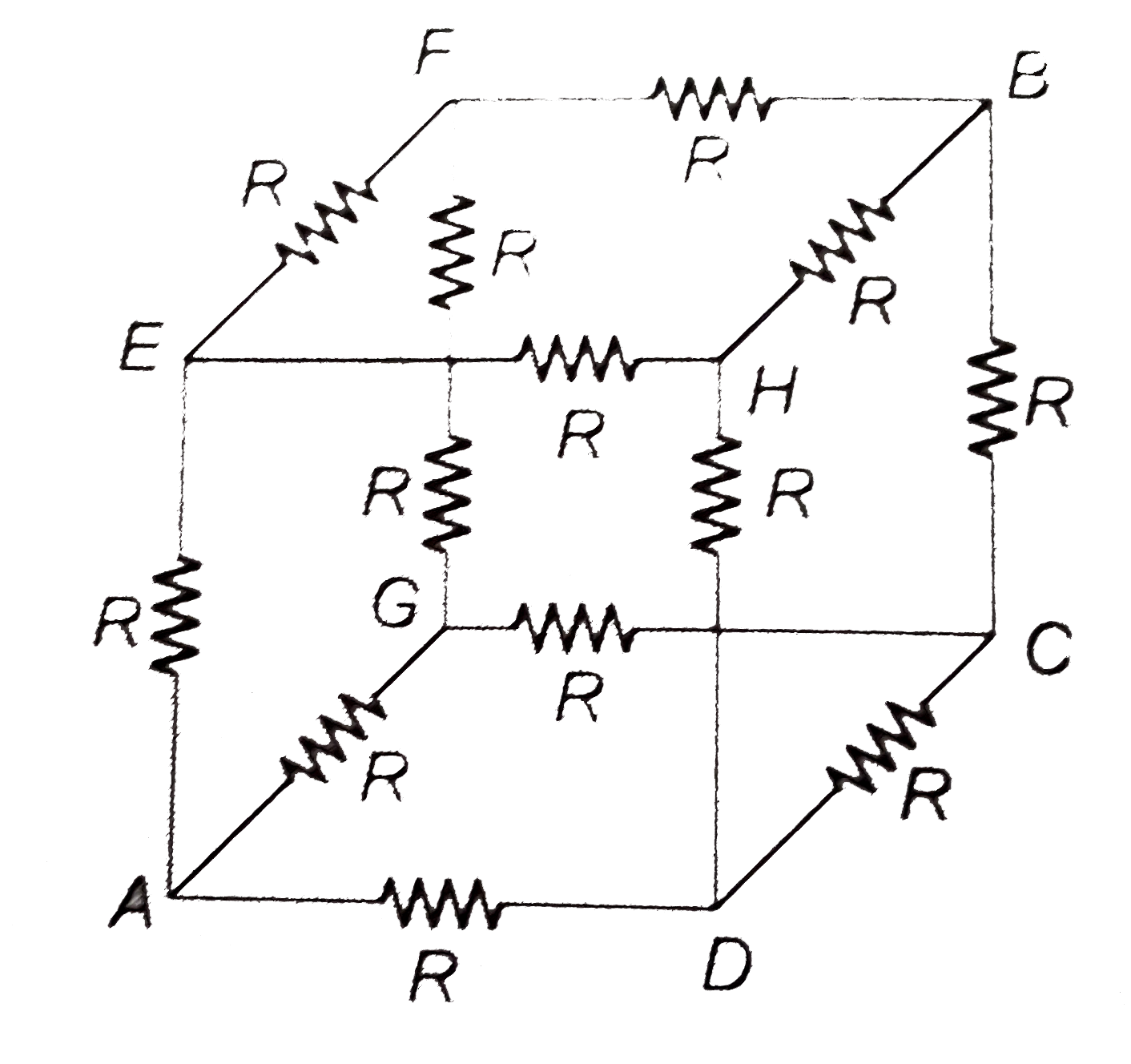
A8r/7B7r/8C3r/4DrEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4
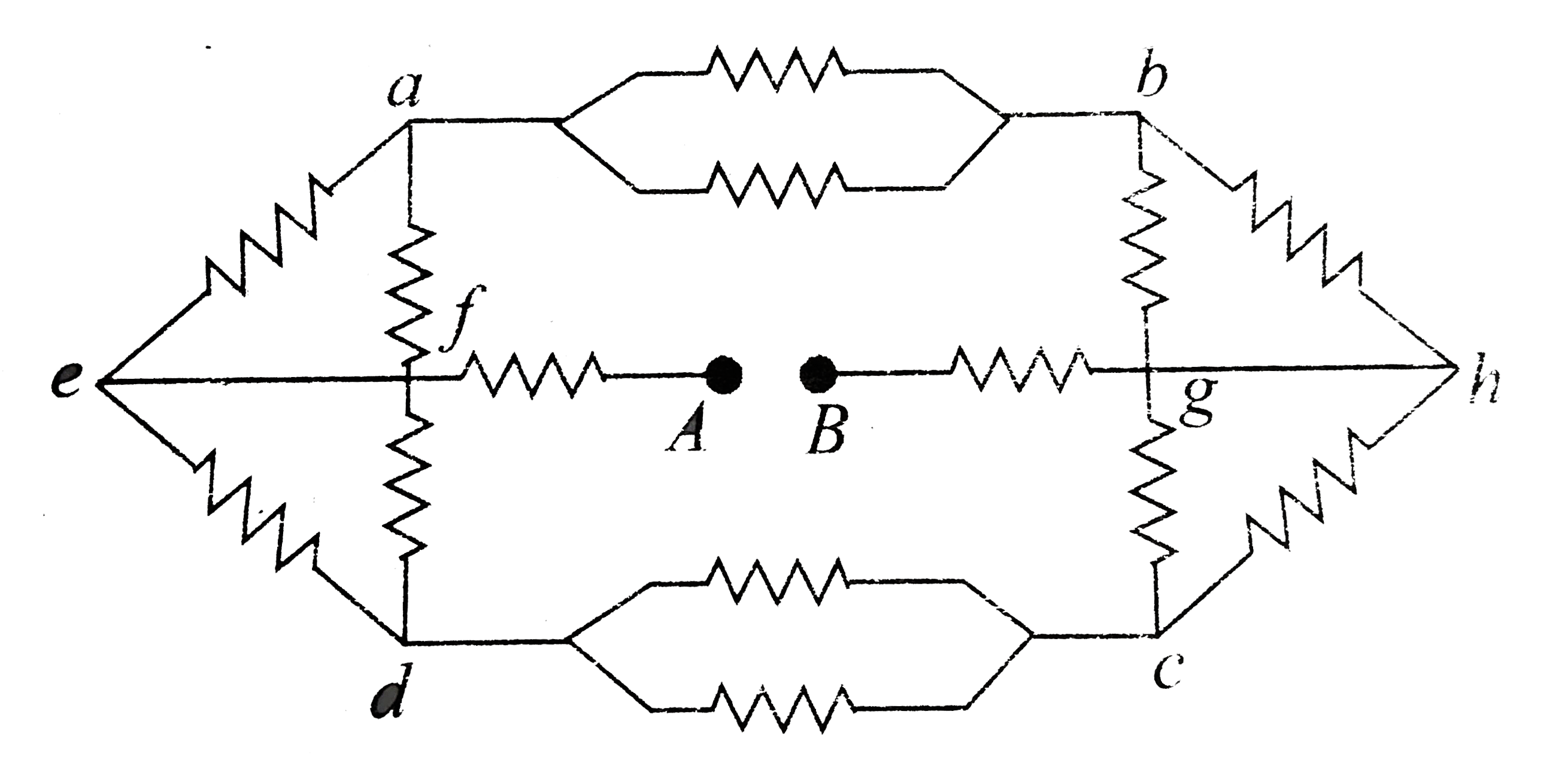
Find the equivalent resistance between point a and b in the network shown in figure.
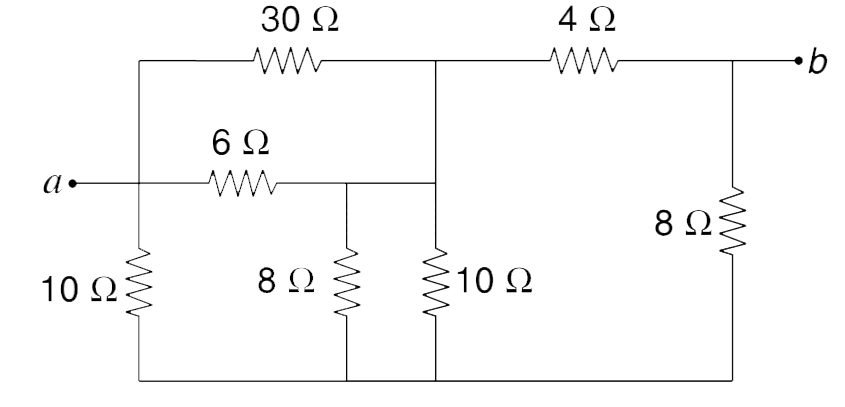
View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is

View SolutionFor the circuit shown in fig. the equivalent resistance between A and C is

View SolutionThe equivalent resistance between A and B in the network in fig.,
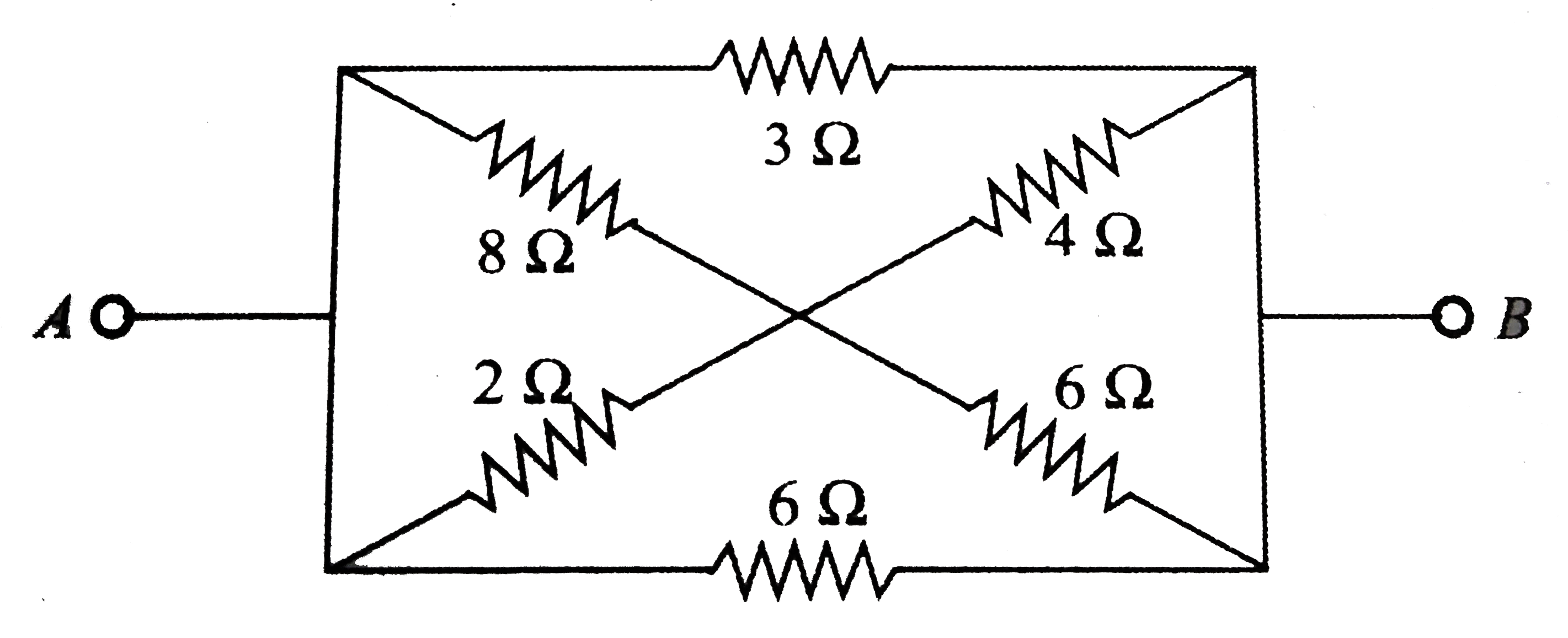
View SolutionThe equivalent resistance between A and B in fig. at steady state will be
View Solution

 .
.