For the equilibrium of a body on an inclined plane of inclination 45∘, the coefficient of static friction will be
greater than one
less than one
zero
less than zero
The correct Answer is:A
To find the coefficient of static friction (μ) for a body in equilibrium on an inclined plane with an inclination of 45∘, we can follow these steps:
Step 1: Identify the Forces Acting on the Body
On an inclined plane, the forces acting on the body include:
- The gravitational force (mg), which can be resolved into two components:
- Perpendicular to the incline: mgcos(45∘)
- Parallel to the incline: mgsin(45∘)
- The normal force (N), which balances the perpendicular component of the weight.
- The frictional force (f), which opposes the motion down the incline and is given by f=μN.
Step 2: Write the Equilibrium Conditions
For the body to be in equilibrium, the net force acting parallel to the incline must be zero. Therefore, we can set up the following equation:
mgsin(45∘)=f
Since the frictional force f is given by f=μN, we can substitute this into the equation:
mgsin(45∘)=μN
Step 3: Calculate the Normal Force
The normal force N is equal to the perpendicular component of the weight:
N=mgcos(45∘)
Step 4: Substitute the Normal Force into the Equation
Now, we can substitute N into the equilibrium equation:
mgsin(45∘)=μ(mgcos(45∘))
Step 5: Simplify the Equation
We can cancel mg from both sides (assuming m≠0):
sin(45∘)=μcos(45∘)
Step 6: Solve for the Coefficient of Static Friction
Now, we can solve for μ:
μ=sin(45∘)cos(45∘)
Using the values of sine and cosine for 45∘:
sin(45∘)=cos(45∘)=1√2
Thus,
μ=1√21√2=1
Conclusion
The coefficient of static friction required for equilibrium on a 45∘ incline is μ=1.
---
On an inclined plane, the forces acting on the body include:
- The gravitational force (mg), which can be resolved into two components:
- Perpendicular to the incline: mgcos(45∘)
- Parallel to the incline: mgsin(45∘)
- The normal force (N), which balances the perpendicular component of the weight.
- The frictional force (f), which opposes the motion down the incline and is given by f=μN.
For the body to be in equilibrium, the net force acting parallel to the incline must be zero. Therefore, we can set up the following equation:
mgsin(45∘)=f
Since the frictional force f is given by f=μN, we can substitute this into the equation:
mgsin(45∘)=μN
The normal force N is equal to the perpendicular component of the weight:
N=mgcos(45∘)
Now, we can substitute N into the equilibrium equation:
mgsin(45∘)=μ(mgcos(45∘))
We can cancel mg from both sides (assuming m≠0):
sin(45∘)=μcos(45∘)
Now, we can solve for μ:
μ=sin(45∘)cos(45∘)
Using the values of sine and cosine for 45∘:
sin(45∘)=cos(45∘)=1√2
Thus,
μ=1√21√2=1
The coefficient of static friction required for equilibrium on a 45∘ incline is μ=1.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTION AND FRICTIONBOOK - BITSAT GUIDECHAPTER - NEWTONS LAWS OF MOTION AND FRICTIONEXERCISE - BITSAT Archives
23 Videos
- MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONBOOK - BITSAT GUIDECHAPTER - MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONEXERCISE - All Questions
86 Videos
- ROTATIONAL MOTIONBOOK - BITSAT GUIDECHAPTER - ROTATIONAL MOTIONEXERCISE - BITSAT Archives
9 Videos
Similar Questions
A solid sphere of mass m rolls without slipping on an inclined plane of inclination 0. what should be the minimum coefficient of static friction to support pure rolling?
View SolutionIf a solid cylinder rolls without slipping on an inclined plane of inclination 45°, then the minimum coefficient of friction required to support pure rolling is
View Solution
Knowledge Check
A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
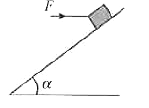 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of theseA block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓A body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
Ag2√2Bg2C3g2√2Dg√2
If a solid cylinder rolls without slipping on an inclined plane of inclination 45° then the minimum coefficient of friction required to support pure rolling is
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View SolutionA solid sphere of mass m rolls without slipping on an inclined plain of inclination θ. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionA body is moving down a long inclined plane in inclination 45∘ with horizontal. The coefficient of friction between the body and the plane varies as μ=x/2, where x is the distance moved down the plane. Initially
x=0&v=0.
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
