For the one dimensional motion, described by x=t−sint
x(t)>0 for all t gt 0
ν(t)>0 for all t>0
a(t)>0 for all t>0
all of these
The correct Answer is:A
To solve the problem of one-dimensional motion described by the equation x=t−sint, we will analyze the position, velocity, and acceleration step by step.
Step 1: Analyze the Position Function
The position function is given by:
x(t)=t−sint
We will evaluate this function for various values of t.
- For t=0:
x(0)=0−sin(0)=0
- For t=π2:
x(π2)=π2−sin(π2)=π2−1
Since π2≈1.57, π2−1>0.
- For t=π:
x(π)=π−sin(π)=π−0=π>0
- For t=2π:
x(2π)=2π−sin(2π)=2π−0=2π>0
From the evaluations, we can see that x(t) is greater than 0 for t>0.
Step 2: Calculate the Velocity
Velocity is the derivative of the position function:
v(t)=dxdt=ddt(t−sint)=1−cost
Now, we will evaluate the velocity for various values of t:
- At t=0:
v(0)=1−cos(0)=1−1=0
- At t=π2:
v(π2)=1−cos(π2)=1−0=1
- At t=π:
v(π)=1−cos(π)=1−(−1)=2
- At t=2π:
v(2π)=1−cos(2π)=1−1=0
The velocity v(t) varies between 0 and 2, indicating that it is not always greater than 0 for t>0.
Step 3: Calculate the Acceleration
Acceleration is the derivative of the velocity function:
a(t)=dvdt=ddt(1−cost)=sint
Now, we will evaluate the acceleration for various values of t:
- At t=0:
a(0)=sin(0)=0
- At t=π2:
a(π2)=sin(π2)=1
- At t=π:
a(π)=sin(π)=0
- At t=2π:
a(2π)=sin(2π)=0
The acceleration a(t) varies between -1 and 1, and is not always 0 for t>0.
Conclusion
Based on the evaluations:
1. The position x(t) is greater than 0 for all t>0.
2. The velocity v(t) is not always greater than 0 for t>0.
3. The acceleration a(t) is not always 0 for t>0.
Thus, the only correct option is that the position is always greater than 0 for all t>0.
The position function is given by:
x(t)=t−sint
We will evaluate this function for various values of t.
x(0)=0−sin(0)=0
- For t=π2:
x(π2)=π2−sin(π2)=π2−1
Since π2≈1.57, π2−1>0.
x(π)=π−sin(π)=π−0=π>0
x(2π)=2π−sin(2π)=2π−0=2π>0
Velocity is the derivative of the position function:
v(t)=dxdt=ddt(t−sint)=1−cost
v(0)=1−cos(0)=1−1=0
v(π2)=1−cos(π2)=1−0=1
v(π)=1−cos(π)=1−(−1)=2
v(2π)=1−cos(2π)=1−1=0
Acceleration is the derivative of the velocity function:
a(t)=dvdt=ddt(1−cost)=sint
a(0)=sin(0)=0
a(π2)=sin(π2)=1
a(π)=sin(π)=0
a(2π)=sin(2π)=0
Based on the evaluations:
1. The position x(t) is greater than 0 for all t>0.
2. The velocity v(t) is not always greater than 0 for t>0.
3. The acceleration a(t) is not always 0 for t>0.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - INSTANTANEOUS VELOCITY AND SPEED
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Force on a particle in one-dimensional motion is given by F=Av+Bt+CxAt+D, where F= force, v= speed, t= time, x= position and A, B, C and D are constants. Dimension of C will be-
View SolutionIn the one-dimensional motion of a particle, the relation between position x and time t is given by x2+2x=t (here x>0). Choose the correct statement
View Solution
Knowledge Check
In one dimensional motion, instantaneous speed v satisfies (0≤v<v0) then
A1. The displacement in time T must always take on-negative values.B2. The displacement x in time T satifies - voT< x < voT.C3. The acceleration is always a non-negative number.D4. The motion has no turning points.The velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval t1 to t2?
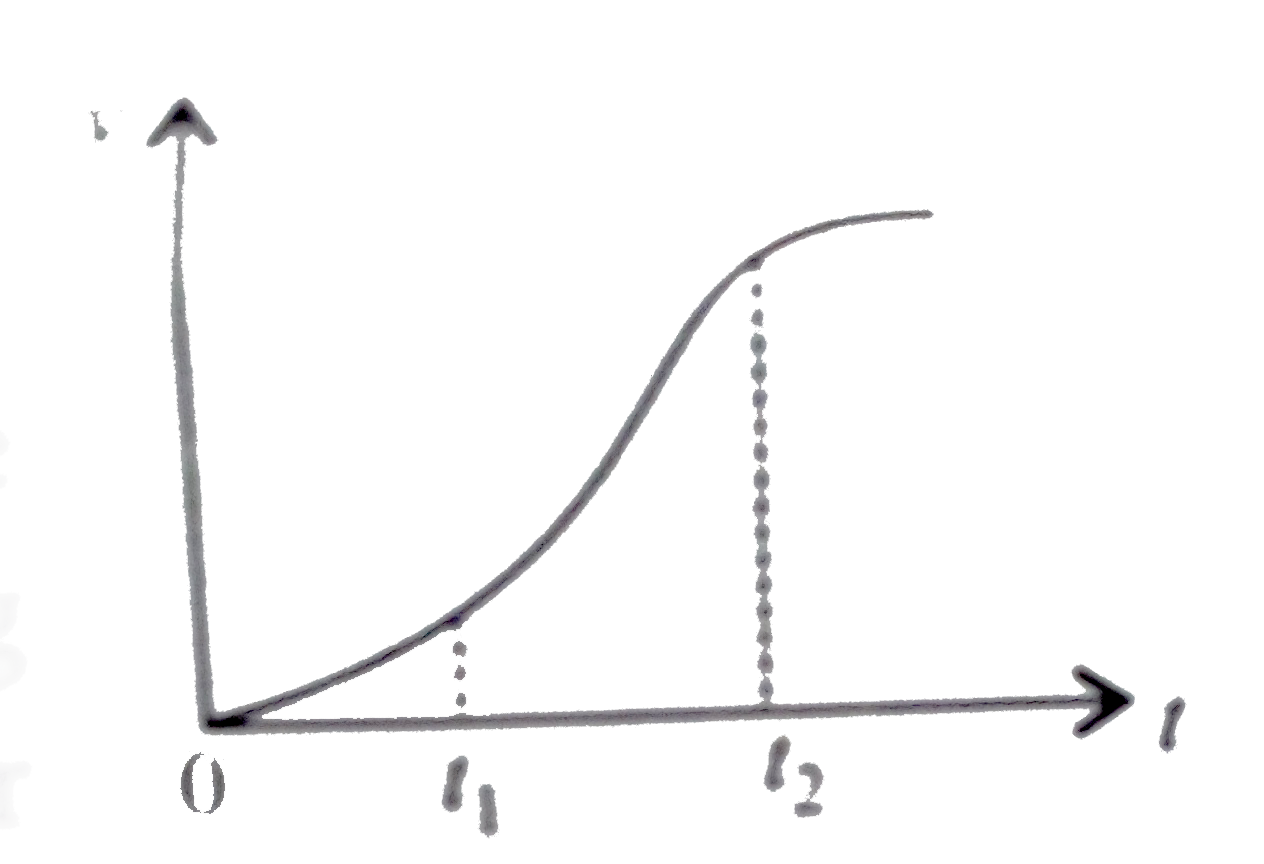 Ax(t2)=x(t1)+v(t1)(t2−t1)+(12)a(t2−t1)2Bv(t2)=v(t1)+a(t2−t1)Cvaverage=x(t2)+x(t1)t2−t1Daaverage=v(t2)−v(t1)t2−t1
Ax(t2)=x(t1)+v(t1)(t2−t1)+(12)a(t2−t1)2Bv(t2)=v(t1)+a(t2−t1)Cvaverage=x(t2)+x(t1)t2−t1Daaverage=v(t2)−v(t1)t2−t1
In one dimensional motion, instantaneous speed v satisfies (0≤v<v0) then
View SolutionA body in one dimensional motion has zero speed at an instant. At that instant, it must have
View SolutionThe linear momentum P of a body varies with time and is given by the equation P=x+yt2, where x and y are constants. The net force acting on the body for a one dimensional motion is proportional to-
View SolutionFig. show the x−t plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least? Give the sign of average speed for each interval.
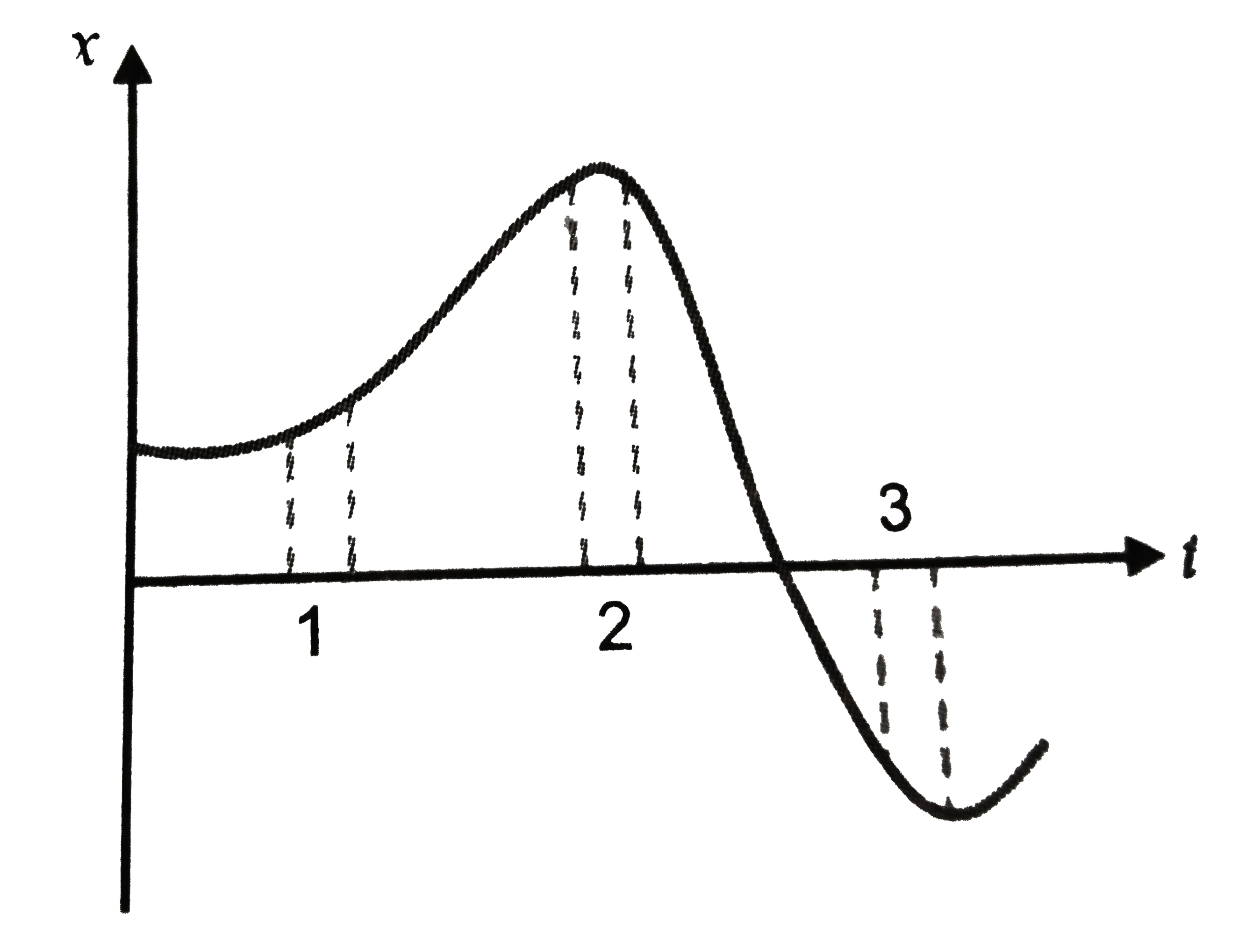 .
.
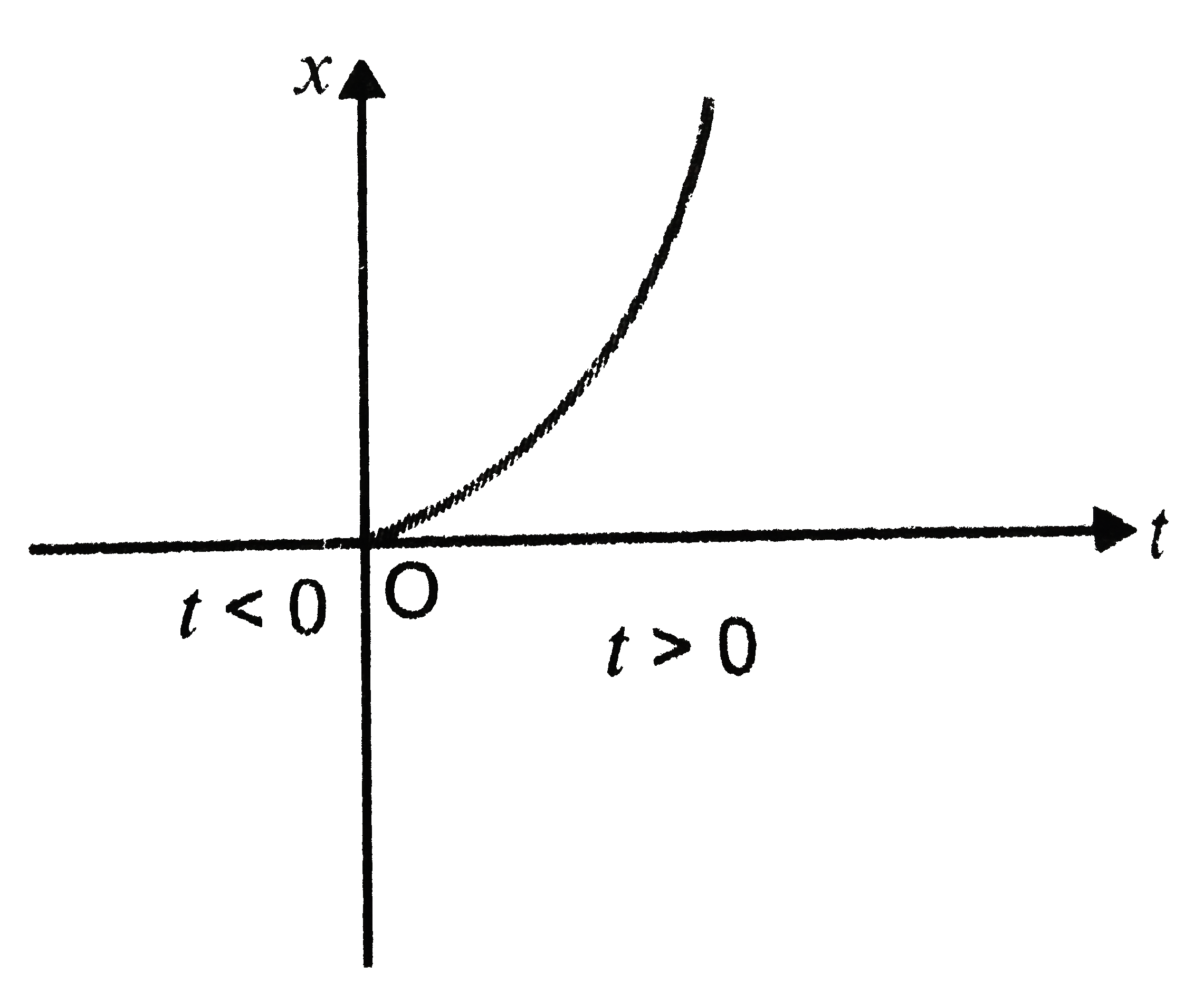
View SolutionFig. shows x−t plot of one dimensional motion a particle. Is it correct to say from the graph that the particle moves in a straight line for t<0 and on a parabolic path form t>0? If not, suggest a suitable physical context for this graph.
View SolutionA body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
View Solution
