For the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

Let F1 and F2 are applied in such a way that m1andm2 do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m1>m2.
(m1+m2)gM+m1+m2
(m1−m2)gM
(m1−m2)gM+m1+m2
F1−F2M
The correct Answer is:C
a=Net forceNet mass=F1−F2M+m1+m2=m1g−m2gM+m1+m2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Find the acceleration of masses m1 and m2 moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
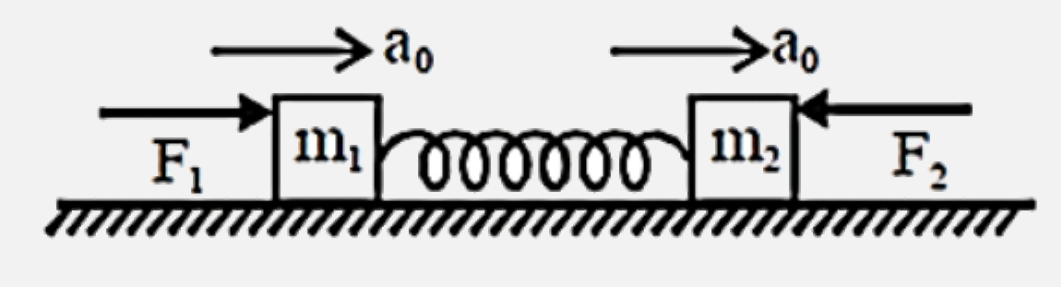 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

According to the above passage, which is correct?AIt is not possible for the entire system to be in equilibrium.BFor some values F1andF2, it is possible that the entire system is in equilibrium.CIt is possble that F1 and F2 are applied in such a way that m1 and m2 remain in equilibrium but M does not.DNone of the above - Question 2 - Select One
In the system shown in fig the pulley is frictionless and the string massless if m1=m2 thrust on the pulley will be:
 Aless than(m1+m2)gBgreater than(m1+m2)gCequal to (m1+m2)gDnone of the above
Aless than(m1+m2)gBgreater than(m1+m2)gCequal to (m1+m2)gDnone of the above - Question 3 - Select One
All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–
 A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2
A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2
What force F must be applied so that m1 and m2 are at rest on m3 in
View SolutionColumn 1 gives four different situations involving two blocks of mass m1andm2 placed in different ways on smooth horizontal surface as shown. In each of the situations, horizontal forces F1andF2 are applied on blocks of mass m1andm2, respectively and also m2F1<m1F2. Match the statements in column I with the corresponding results in column II.
 View Solution
View SolutionIn the system shown in the fig. there is no friction and string is light. Mass of movable pulley P2isM2. If pulley P1 is massless, what should be value of applied force F to keep the system in equilibrium?
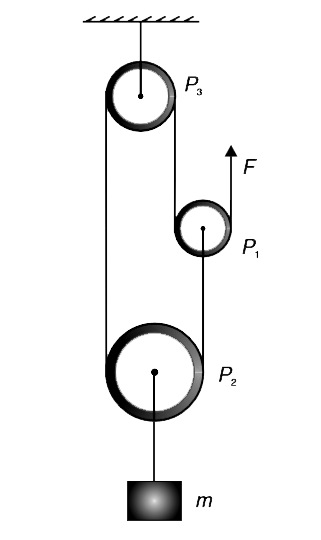 View Solution
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be
 View Solution
View SolutionIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
View Solution

