For the wave described in the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs ? In which aspects does the oscillatory motion in a travelling wave differ from one point to another : amplitude, frequency or phase ?
y(x,t)=3sin[36t+0.018x+π4]
For x = 0
y(0,t)=3sin[36t+0.018×0+π4]
=3sin[36t+π4]
ω=36,2πT=36
T=2π36orT=π18 sec.
For different values of t, the calculated values of y are tabulated as
t0T/82T/83T/84T/85T/86T/87T/8Ty3√233√20−3√2−3−3√203√2

Similarly, we can get (y, t) graphs for x = 2 cm and x = 4 cm. All the curves are sinusoidal in nature. They have same amplitude, same frequency but different initial phase.
Topper's Solved these Questions
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - NCERT ADDITIONAL EXERCISES
6 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - NCERT EXEMPLAR PROBLEMS
31 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CONCEPTUAL QUESTIONS
25 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
For the wave described in exercise 27 plot the displacement (y) versus (t) graphs for x=0,2 and 4m. What are the shaps of these graphs ? In which aspects does the oscillatory motion in travelling wave differ from one point to another amplitude, frequency or phase?
View SolutionFor the wave y= 3.0 sin(36t + 0.018x + pi/4) plot the displacement (y) versus (t) graphs for x=0,. What is the shaps of the graph ? In which aspects does the oscillatory motion in travelling wave differ from one point to another amplitude, frequency or phase?
View Solution
Knowledge Check
For the harmonic travelling wave y=2cos2pi(10t-0.0080x+3.5) where x and y ar in cm and t is in second. What is the phase diffference between the oscillatory motion at two points separated by a distance of
A4mB0.5mCλ2D3λ4 (at a given instant of time)The equation y=4+2sin(6t−3x) represents a wave motion. Then, wave speed and amplitude, respectively are
Awave speed 1 unit, amplitude 6 unitBwave speed 2 unit, amplitude 2 unitCwave speed 4 unit, amplitude 1/2 unitDwave speed 1/2 unit, amplitude 5 unitFor the travelling harmonic wave
y(x, t) = 2 cos2π(10t - 0.008x + 0.35) where X and Y are in cm and t is in s. The phase difference between oscillatory motion of two points separated by distance of 0.5 m isA0.2πradB0.4πradC0.6πradD0.8πrad
For the harmonic travelling wave y=2cos2pi(10t-0.0080x+3.5) where x and y ar in cm and t is in second. What is the phase diffference between the oscillatory motion at two points separated by a distance of
View SolutionIn the following graph. the displacements of a particle of a progressive wave at different times are shown. Refer to this graph and answer the questions given below.
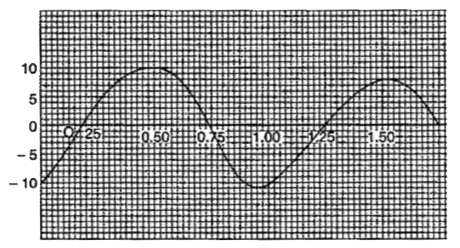
Which one ·or the following is the amplitude of the wave?
View SolutionA transverse harmonic wave on a string is described by y(x,t)=3.0sin(36t+0.018n+π/4), where x and y are in cm an t in sec. The positive direction of x is from left to right.
(a) Is this a travelling wave or a stationary wave?
(b) What are its amplitude and frequency?
View Solutiongraphs of the same harmonic wave are shown below. The graph (1) on the left shows the displacement of wave y, as a function of position x for a given instant of time. The graph (2) on the right shows the displacement of wave as a function to time 't' for a given position. The speed of the wave is
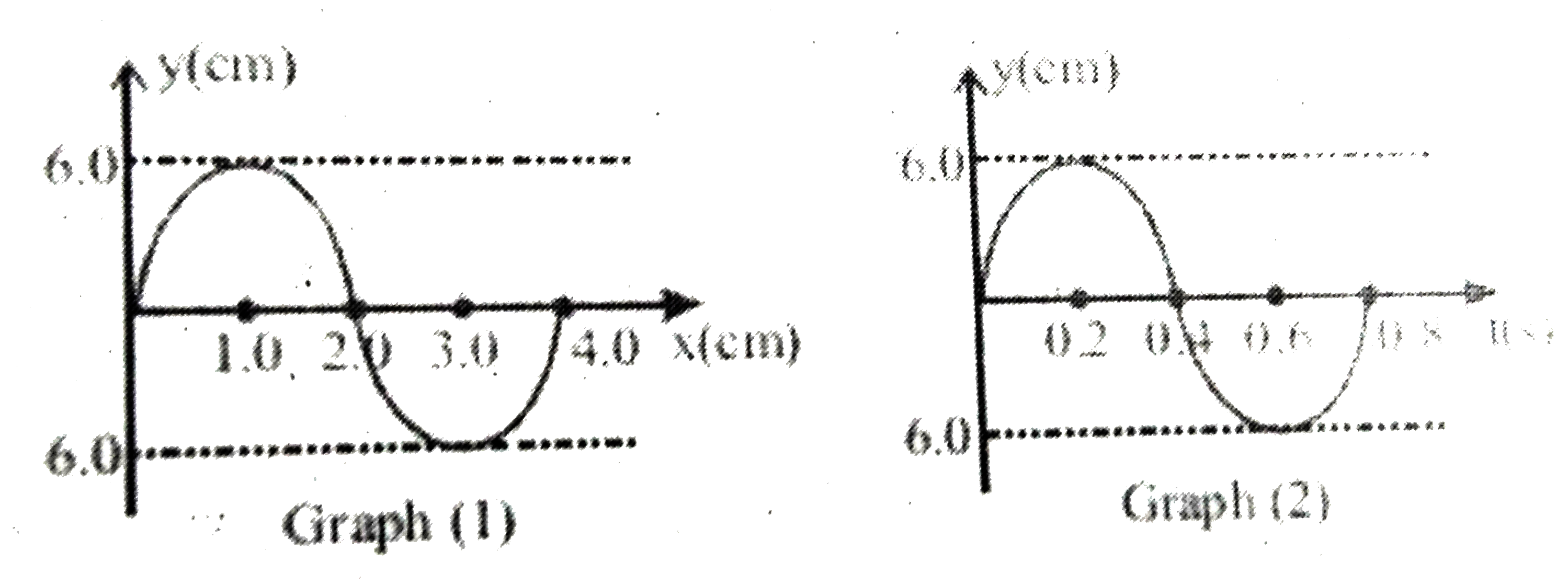
View SolutionFor the travelling harmonic wave
y(x, t) = 2 cos2π(10t - 0.008x + 0.35) where X and Y are in cm and t is in s. The phase difference between oscillatory motion of two points separated by distance of 0.5 m is
View Solution
