Force acting on a block moving along x-axis is given by
F=−(4x2+2)N
The block is displaced from x=−2m to x=+4m, the work done will be
positive
negative
zero
may be positive or negative
The correct Answer is:B
To find the work done on the block as it moves from x=−2m to x=4m under the influence of the force F=−4x2+2N, we will follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a variable force along a straight path is given by the integral of the force over the displacement:
W=∫x2x1Fdx
where x1 is the initial position and x2 is the final position.
Step 2: Set Up the Integral
In this case, we need to calculate:
W=∫4−2−4x2+2dx
Step 3: Evaluate the Integral
We can simplify the integral:
W=−4∫4−21x2+2dx
The integral ∫1x2+a2dx is known to be 1atan−1(xa)+C. Here, a2=2 implies a=√2.
Thus, we have:
∫1x2+2dx=1√2tan−1(x√2)+C
Step 4: Calculate the Definite Integral
Now we need to evaluate:
W=−4(1√2tan−1(x√2))4−2
Calculating the limits:
1. For x=4:
tan−1(4√2)=tan−1(2√2)
2. For x=−2:
tan−1(−2√2)=tan−1(−√2)
Step 5: Substitute the Limits
Now substituting the limits into the integral:
W=−4(1√2(tan−1(2√2)−tan−1(−√2)))
Step 6: Simplify the Expression
Using the property of the arctangent function:
tan−1(−x)=−tan−1(x)
Thus:
W=−4(1√2(tan−1(2√2)+tan−1(√2)))
Step 7: Final Calculation
Now we can compute the numerical values of tan−1(2√2) and tan−1(√2) using a calculator and substitute them back into the equation to find the work done.
Conclusion
The work done W will be negative since the force is acting opposite to the direction of displacement.
The work done W by a variable force along a straight path is given by the integral of the force over the displacement:
W=∫x2x1Fdx
where x1 is the initial position and x2 is the final position.
In this case, we need to calculate:
W=∫4−2−4x2+2dx
We can simplify the integral:
W=−4∫4−21x2+2dx
The integral ∫1x2+a2dx is known to be 1atan−1(xa)+C. Here, a2=2 implies a=√2.
∫1x2+2dx=1√2tan−1(x√2)+C
Now we need to evaluate:
W=−4(1√2tan−1(x√2))4−2
1. For x=4:
tan−1(4√2)=tan−1(2√2)
tan−1(−2√2)=tan−1(−√2)
Now substituting the limits into the integral:
W=−4(1√2(tan−1(2√2)−tan−1(−√2)))
Using the property of the arctangent function:
tan−1(−x)=−tan−1(x)
Thus:
W=−4(1√2(tan−1(2√2)+tan−1(√2)))
Now we can compute the numerical values of tan−1(2√2) and tan−1(√2) using a calculator and substitute them back into the equation to find the work done.
The work done W will be negative since the force is acting opposite to the direction of displacement.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:A Only One Option is Correct
Explore 42 Videos
- WORK, POWER AND ENERGYBook:DC PANDEY ENGLISHChapter:WORK, POWER AND ENERGYExercise:B More than One Option is Correct
Explore 26 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Consider a variable force F=(3x+5)N acting on a body and if it is displaced from x=2m to x=4m, calculate the work done by this force.
View SolutionA force→F=(7−2x+3x2) N is applied on a 2 kg mass which displaces it from x = 0 to x = 5 m. Work done in joule is -
View SolutionA positon dependent force ,F=8−4x+3x2N acts on a small body of mass 2 kg and displaces it from x=0 to x=5 m. The work done in joule is
View SolutionThe velocity of a block of mass 2kg moving along x− axis at any time t is givne by v=20−10t(m/s) where t is in seconds and v is in m/s. At time t=0, the block is moving in positive x− direction.
The Kinetic energy of block at t=3sec. is :
View SolutionThe velocity of a block of mass 2kg moving along x− axis at any time t is givne by v=20−10t(m/s) where t is in seconds and v is in m/s. At time t=0, the block is moving in positive x− direction.
The work done by net force on the block starting from t=0 till it covers a distance 25 metres will be :
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionA force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
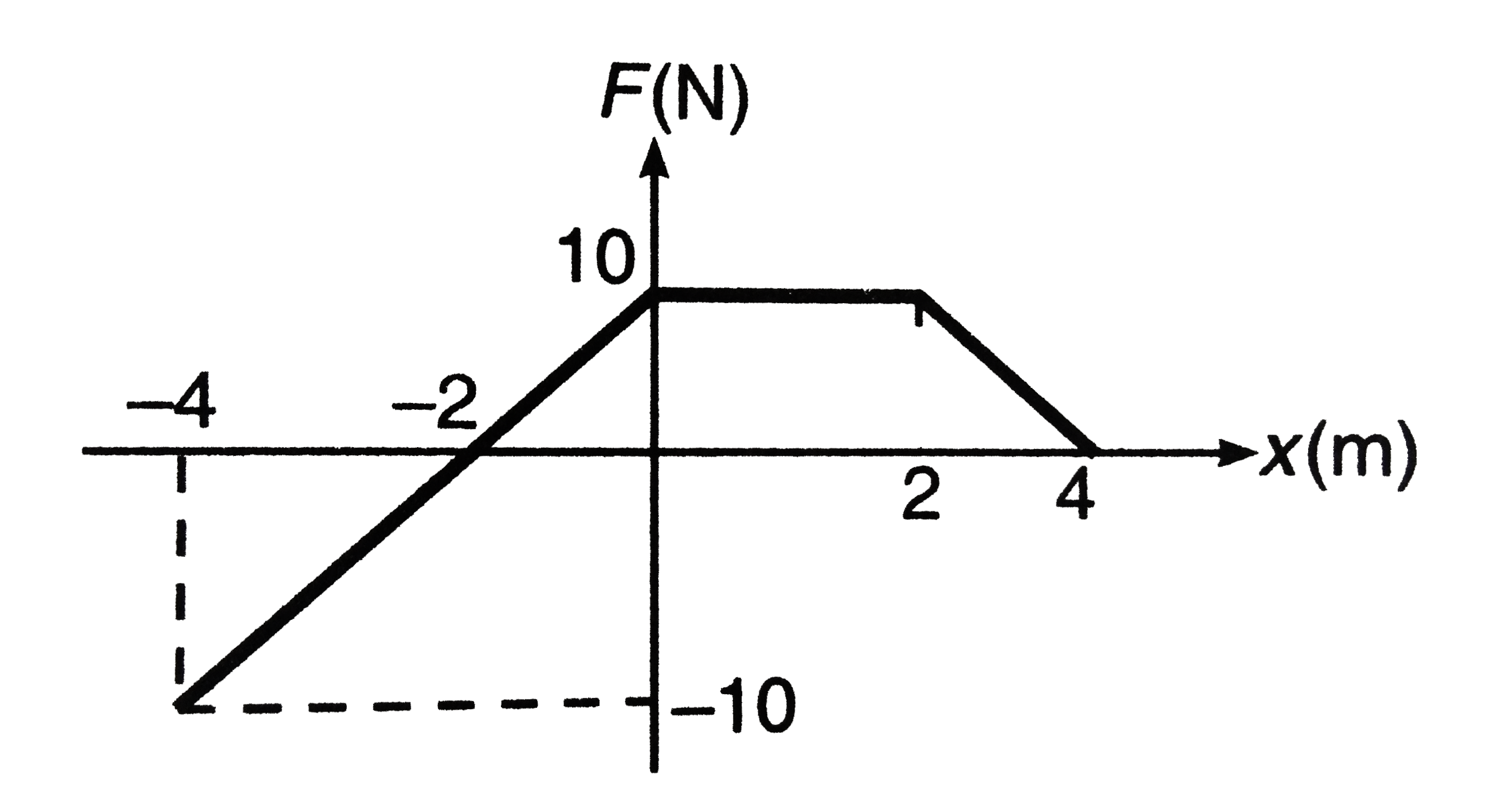 .
.
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View Solution