Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. If O is the center of square.
The electric field at O is.
q√2πε0a2
q√3πε0a2
√3qπε0a2
√2qπε0a2
The correct Answer is:D
To find the electric field at the center O of a square formed by four charges +q,+q,−q,−q at the corners A,B,C, and D respectively, we can follow these steps:
Step 1: Identify the charges and their positions
- Place the charges at the corners of the square:
- Charge +q at corner A (top left)
- Charge +q at corner B (top right)
- Charge −q at corner C (bottom right)
- Charge −q at corner D (bottom left)
Step 2: Determine the distance from the center O to each charge
- The distance from the center O to each corner of the square is given by:
r=a√2
where a is the side length of the square.
Step 3: Calculate the electric field due to each charge at point O
- The electric field E due to a point charge q at a distance r is given by:
E=k|q|r2
where k is Coulomb's constant (k=14πϵ0).
- For each charge, the electric field at O can be calculated:
- For charges +q at A and B:
EA=EB=kq(a√2)2=2kqa2
(directed away from the charges)
- For charges −q at C and D:
EC=ED=kq(a√2)2=2kqa2
(directed towards the charges)
Step 4: Determine the direction of the electric fields
- The electric field EA and EB are directed away from A and B respectively, while EC and ED are directed towards C and D respectively.
Step 5: Resolve the electric fields into components
- The electric fields EA and EB will have components along the x-axis and y-axis:
- For EA (upward and left):
EAx=−EAcos(45∘)=−2kqa2⋅1√2=−2kqa2√2
EAy=EAsin(45∘)=2kqa2⋅1√2=2kqa2√2
- For EB (upward and right):
EBx=EBcos(45∘)=2kqa2⋅1√2=2kqa2√2
EBy=EBsin(45∘)=2kqa2⋅1√2=2kqa2√2
- For EC and ED (downward):
- The components will be:
ECx=ECcos(45∘)=2kqa2⋅1√2=2kqa2√2
ECy=−ECsin(45∘)=−2kqa2⋅1√2=−2kqa2√2
- For ED:
EDx=−EDcos(45∘)=−2kqa2⋅1√2=−2kqa2√2
EDy=−EDsin(45∘)=−2kqa2⋅1√2=−2kqa2√2
Step 6: Sum the components of the electric fields
- The x-components:
Enetx=EAx+EBx+ECx+EDx=−2kqa2√2+2kqa2√2+2kqa2√2−2kqa2√2=0
- The y-components:
Enety=EAy+EBy+ECy+EDy=2kqa2√2+2kqa2√2−2kqa2√2−2kqa2√2=0
Final Result
- The net electric field at point O is:
Enet=Enetx+Enety=0+0=0
- Place the charges at the corners of the square:
- Charge +q at corner A (top left)
- Charge +q at corner B (top right)
- Charge −q at corner C (bottom right)
- Charge −q at corner D (bottom left)
- The distance from the center O to each corner of the square is given by:
r=a√2
where a is the side length of the square.
- The electric field E due to a point charge q at a distance r is given by:
E=k|q|r2
where k is Coulomb's constant (k=14πϵ0).
- For charges +q at A and B:
EA=EB=kq(a√2)2=2kqa2
(directed away from the charges)
EC=ED=kq(a√2)2=2kqa2
(directed towards the charges)
- The electric field EA and EB are directed away from A and B respectively, while EC and ED are directed towards C and D respectively.
- The electric fields EA and EB will have components along the x-axis and y-axis:
- For EA (upward and left):
EAx=−EAcos(45∘)=−2kqa2⋅1√2=−2kqa2√2
EAy=EAsin(45∘)=2kqa2⋅1√2=2kqa2√2
EBx=EBcos(45∘)=2kqa2⋅1√2=2kqa2√2
EBy=EBsin(45∘)=2kqa2⋅1√2=2kqa2√2
- The components will be:
ECx=ECcos(45∘)=2kqa2⋅1√2=2kqa2√2
ECy=−ECsin(45∘)=−2kqa2⋅1√2=−2kqa2√2
EDx=−EDcos(45∘)=−2kqa2⋅1√2=−2kqa2√2
EDy=−EDsin(45∘)=−2kqa2⋅1√2=−2kqa2√2
- The x-components:
Enetx=EAx+EBx+ECx+EDx=−2kqa2√2+2kqa2√2+2kqa2√2−2kqa2√2=0
Enety=EAy+EBy+ECy+EDy=2kqa2√2+2kqa2√2−2kqa2√2−2kqa2√2=0
- The net electric field at point O is:
Enet=Enetx+Enety=0+0=0
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. If O is the center of square.
The electric field at O is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric potential at O is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to F is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to E is.
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionFour point charge q,−q,2Q and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of q/Q is 5√5x. Find the value of x.
View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
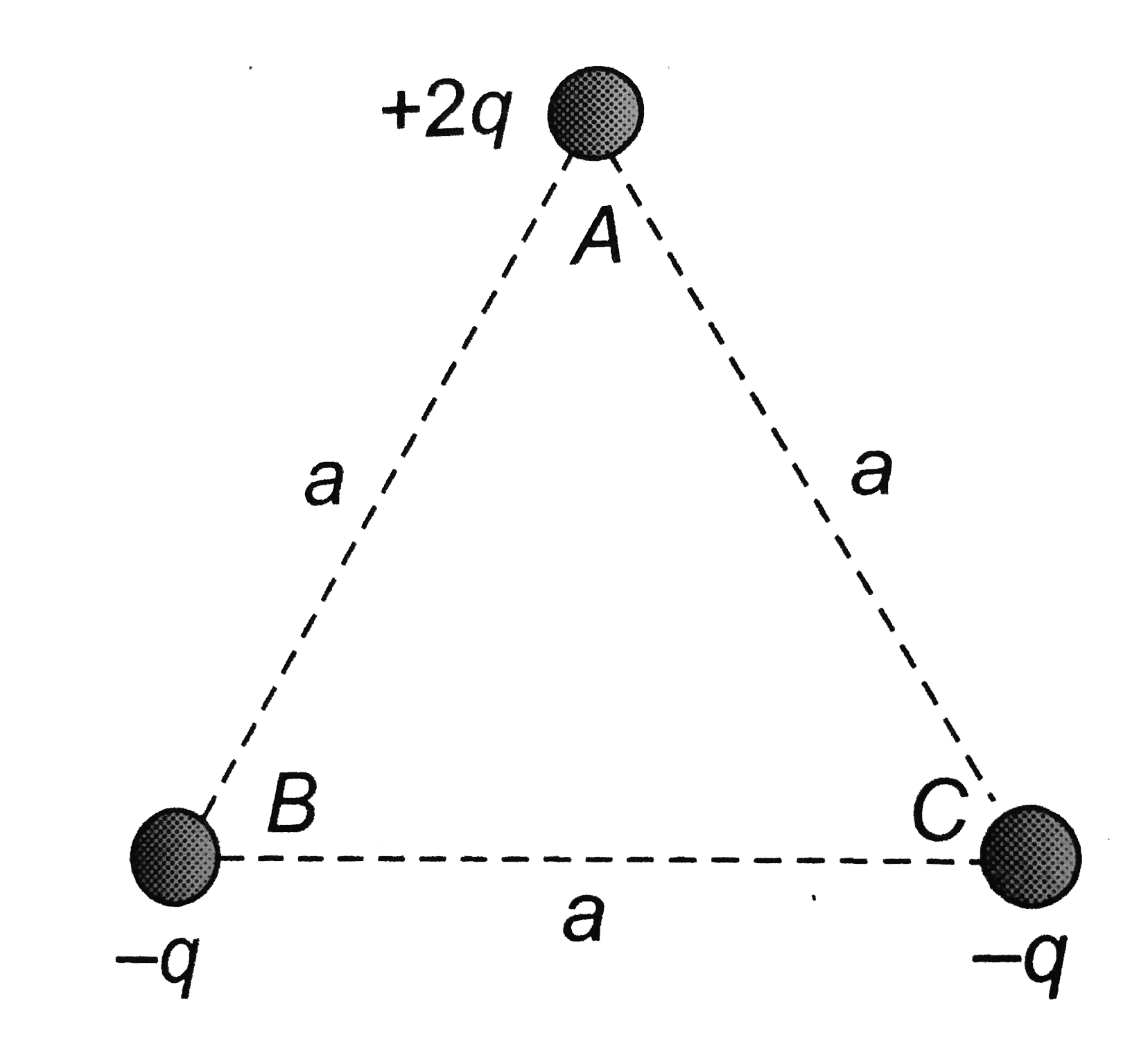
View Solution
