The electrical potential function for an electrical field directed parallel to the x-axis is shown in the given graph.
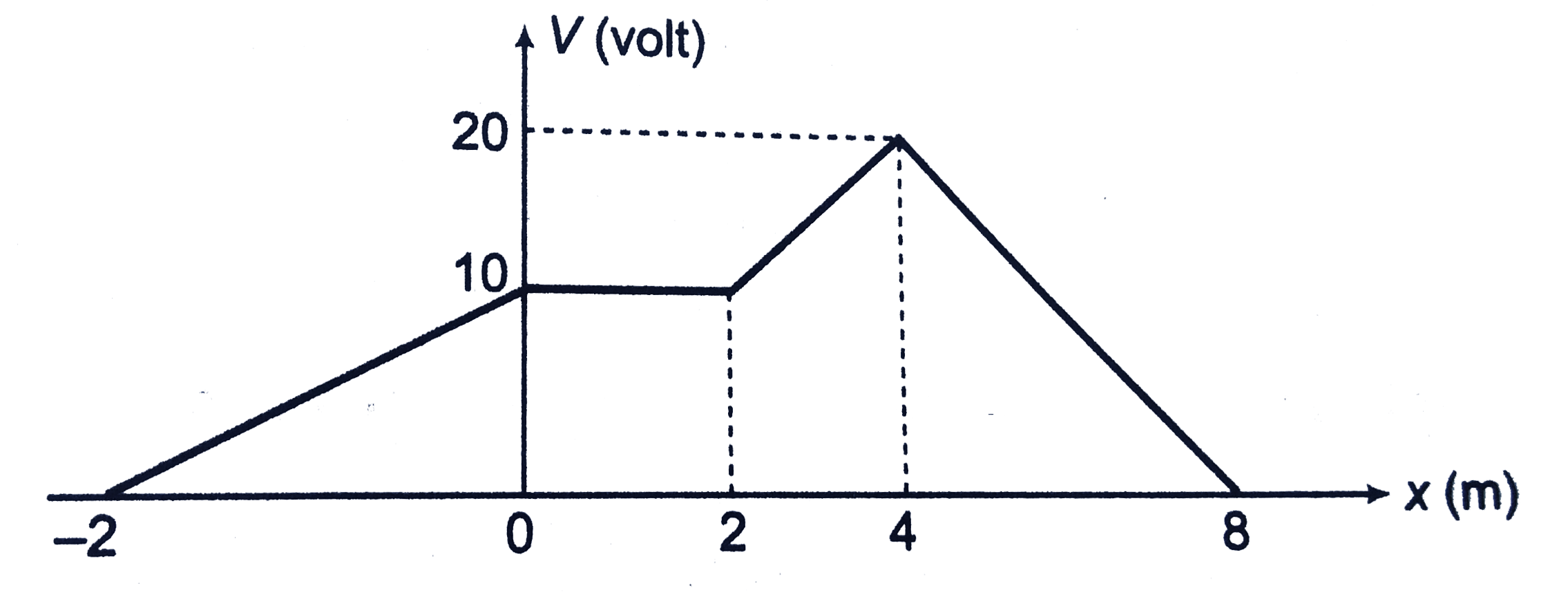 Draw the graph of electric field strength.
Draw the graph of electric field strength.

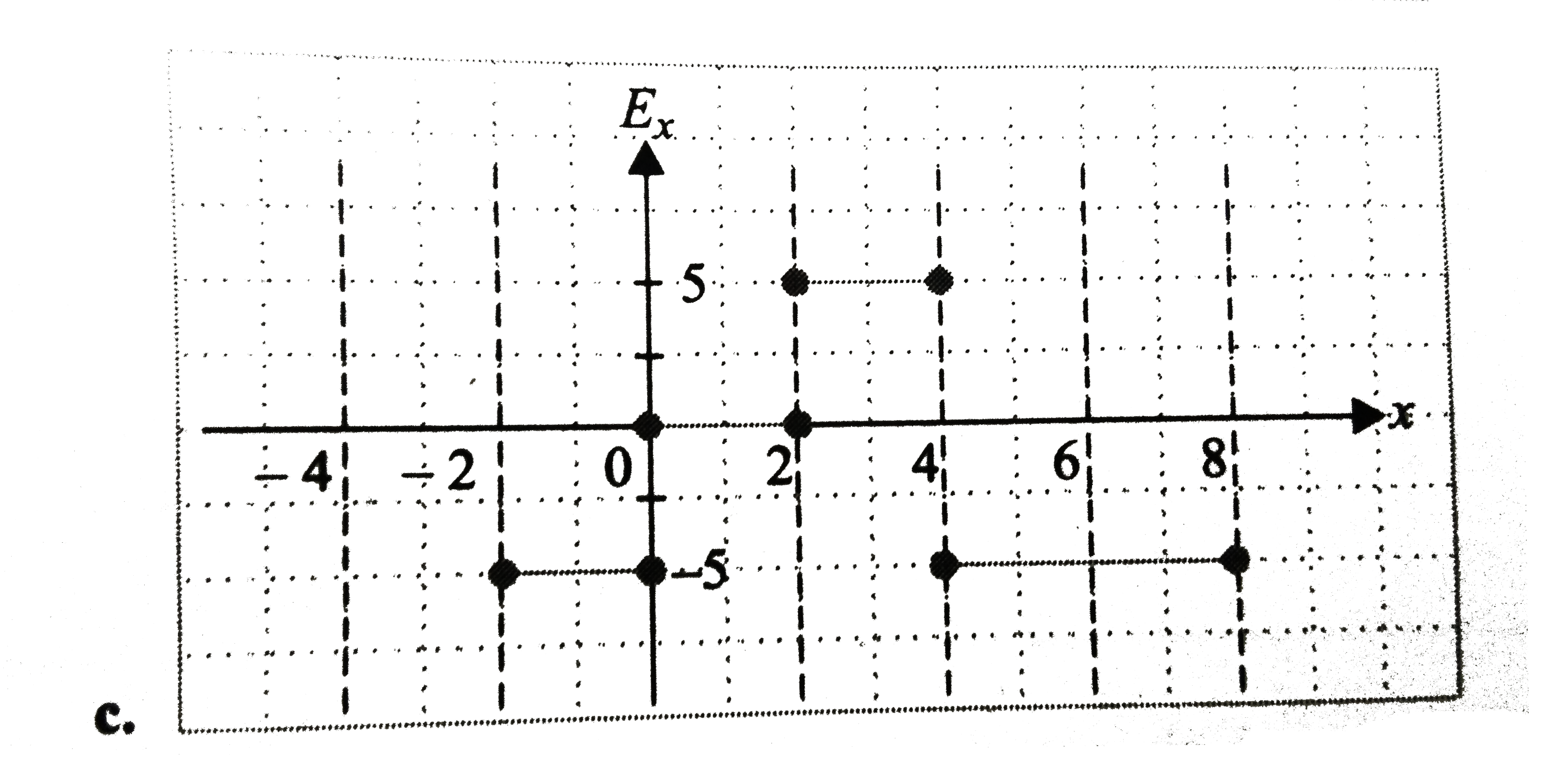
The correct Answer is:A
Er=−ΔVΔr,Ex=−ΔVΔx
For −2≤x≤0,Ex=−(10−0)[0−(−2)]=−5NC−1
For 0≤x≤2,Ex=0
For 2≤x≤4,Ex=−[20−10][4−2]=−5NC−1
For 4≤x≤8,Ex=−[0−20][8−4]=5NC−1
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
The variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
 .
.
View SolutionDue to an electric dipole shown in fig., the electric field intensity is parallel to dipole axis :

View SolutionA uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
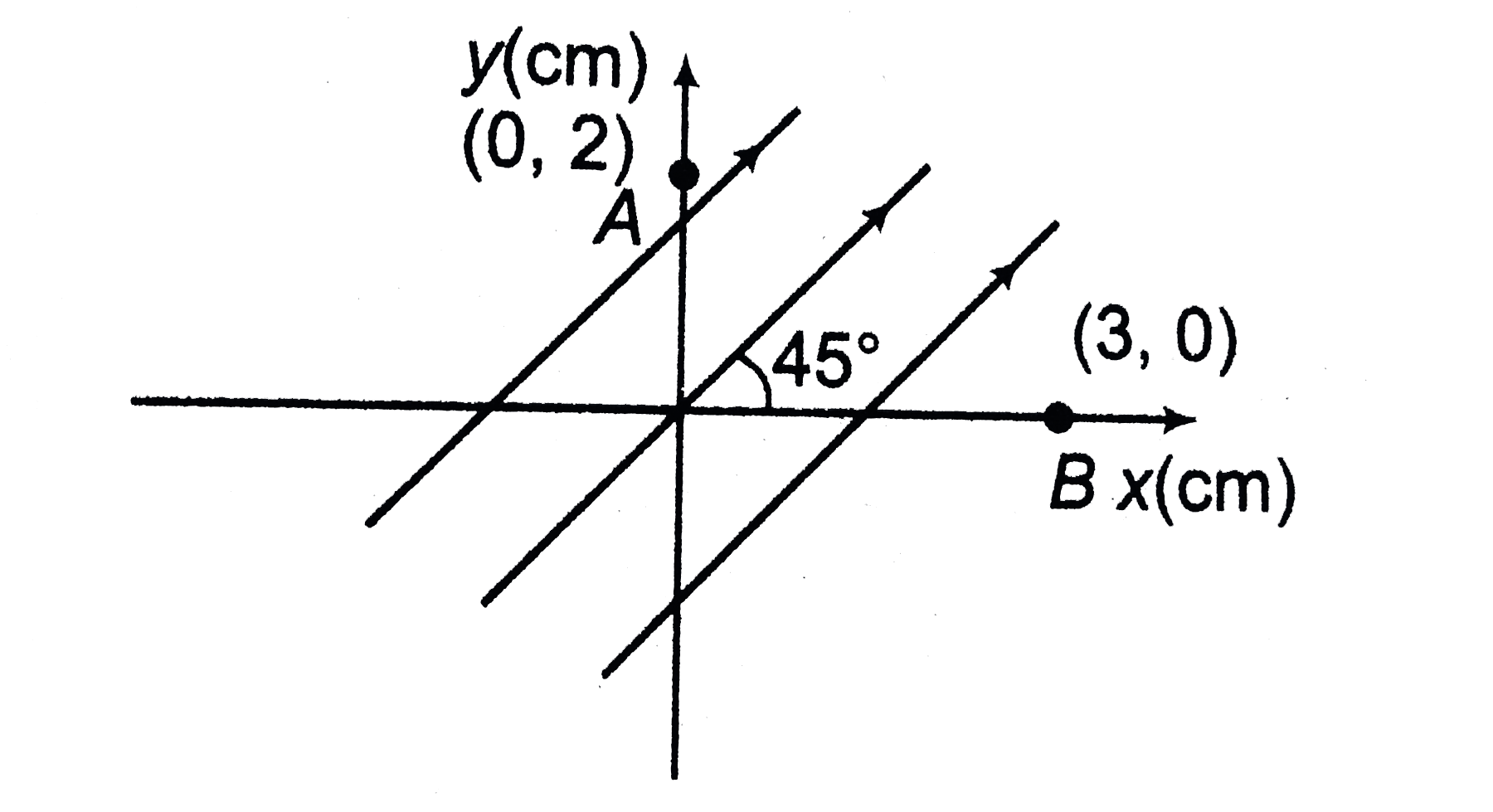
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
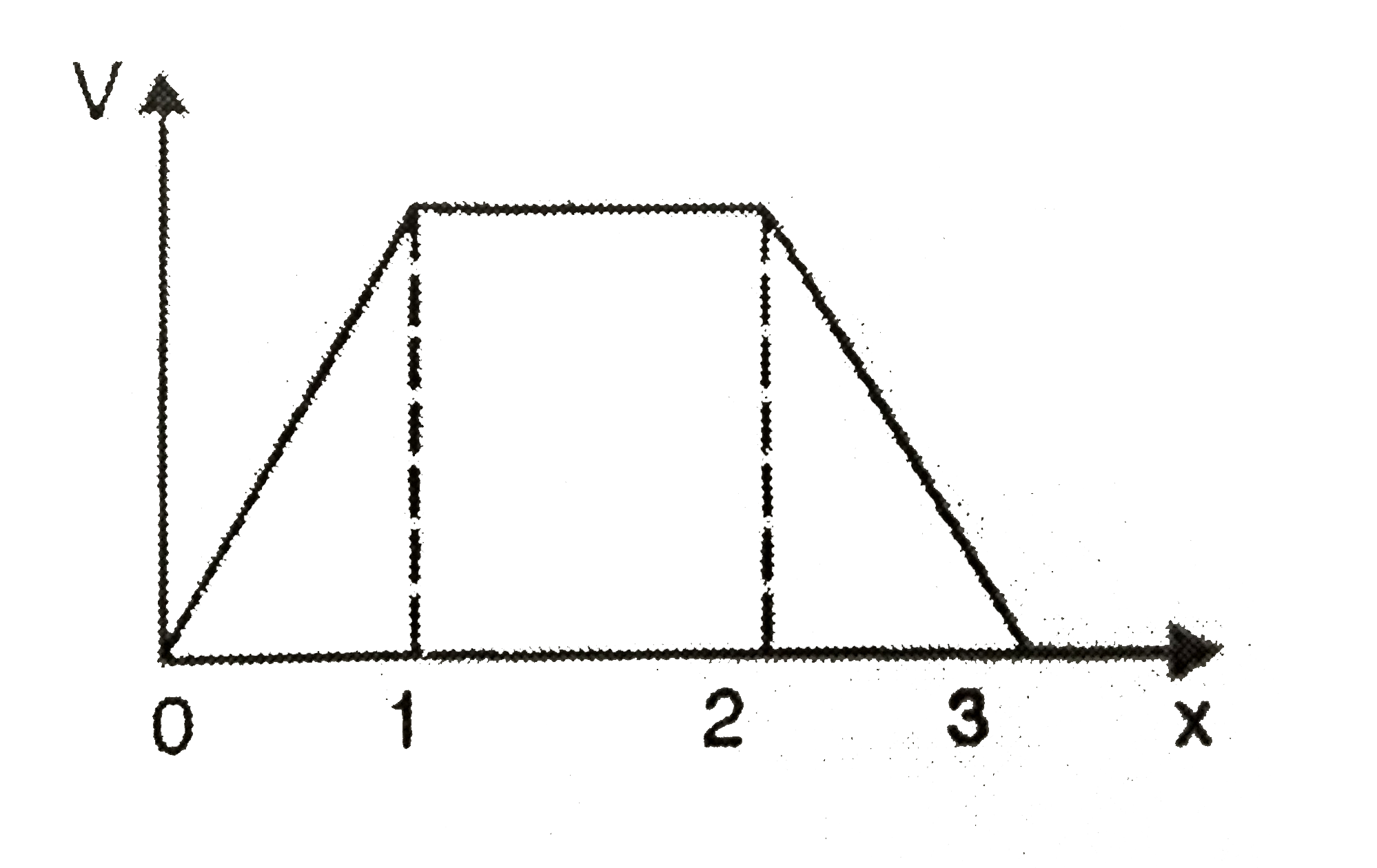
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
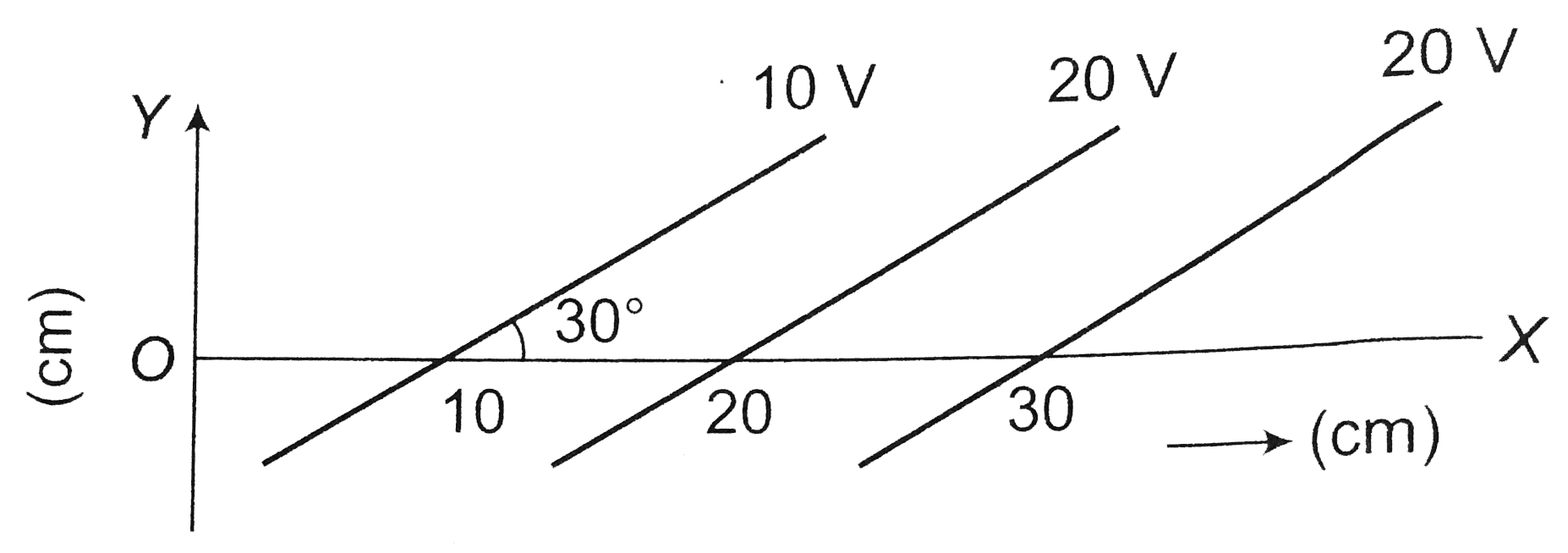
View SolutionEquipotential surfaces are shown in figure. Then the electric field strength will be
View SolutionAt time t1, an electron is sent along the positive direction of x-axis through both an electric field and a magnetic field, with directed parallel to the y-axis Graph gives the y-component Emax of the net force on the electron due to the two fields, as a function of th eelectron's speed V at time t1. Assuming Bx=0, find magnitude of electric field in mN//C and find z component of magnetic field also (Use e=1.6×10−19C)

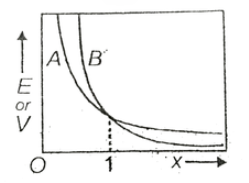
View SolutionA charge (+Q) is placed at the origin O . Variation of electric potential V and magnitude of electric field E along the x-axis is plotted,as shown , in the form of two curves A and B ,then curve A represents the variation of
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionAn electric dipole is placed in an uniform electric field with the dipole axis making an angle θ with the direction of the electric field. The orientation of the dipole for stable equilibrium is
View SolutionFind the direction of electric field at P for the charge distribution as shown infigure.
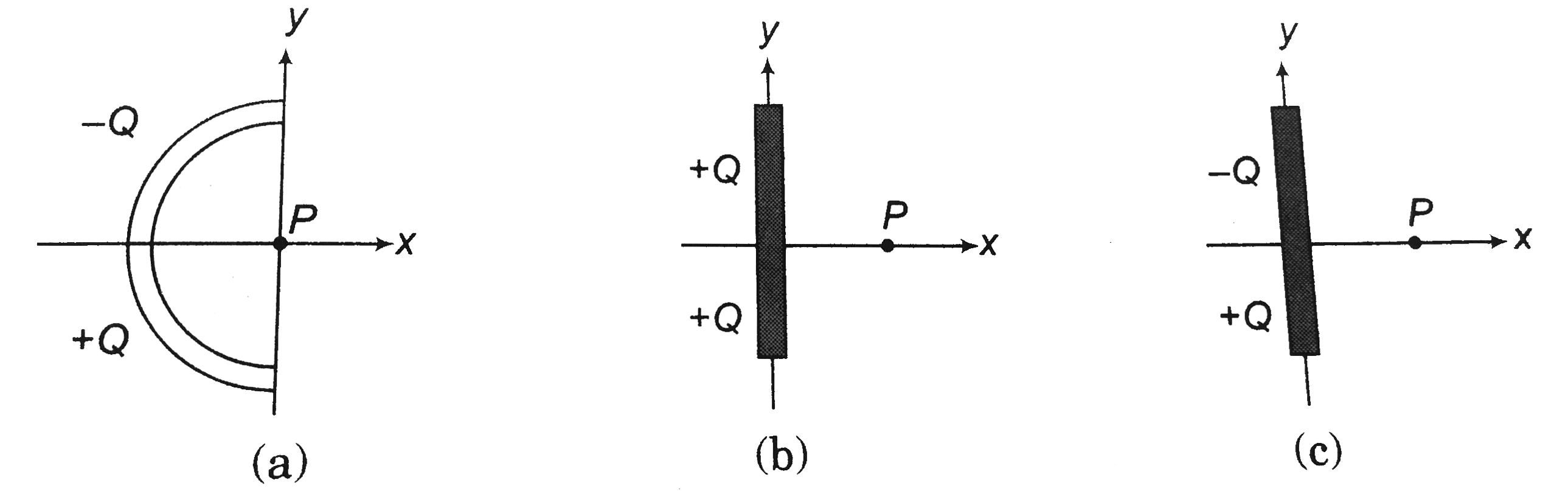
View Solution