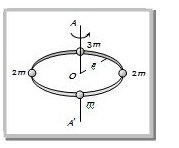
Four masses are rotated about an axis as shown. What is the radius of gyration of the system ?

r
r2
r4
√2r
The correct Answer is:A
Moment of inertia of a mass about an axis = Mass x (Distance)2
∴ Moment of inertia of masses are
I1=2mr2,I2=3mr2,I3=2mr2andI4=mr2
So, total moment of inertia of system of masses
=I1+I2+I3+I4=8πr2
Total mass of system = 8m
If radius of gyration is K, then I=MK2
or K2=IM=8mr28morK=?
Topper's Solved these Questions
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
70 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))
47 Videos
- REFRACTION OF LIGHTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 2
25 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
Similar Questions

Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View Solution
Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View Solution
Knowledge Check

Find the moment of inertia of a solid sphere of mass M and radias R about an axis XX shown in figure.A75MR2B45MR2C35MR2D25MR2Four masses are joined to a light circular frame as shown in the figure. The radius of gyration of this system about an axis passing through the centre of the circular frame and perpendicular to its plane would be
 Aa/√2Ba/2CaD2a
Aa/√2Ba/2CaD2aThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
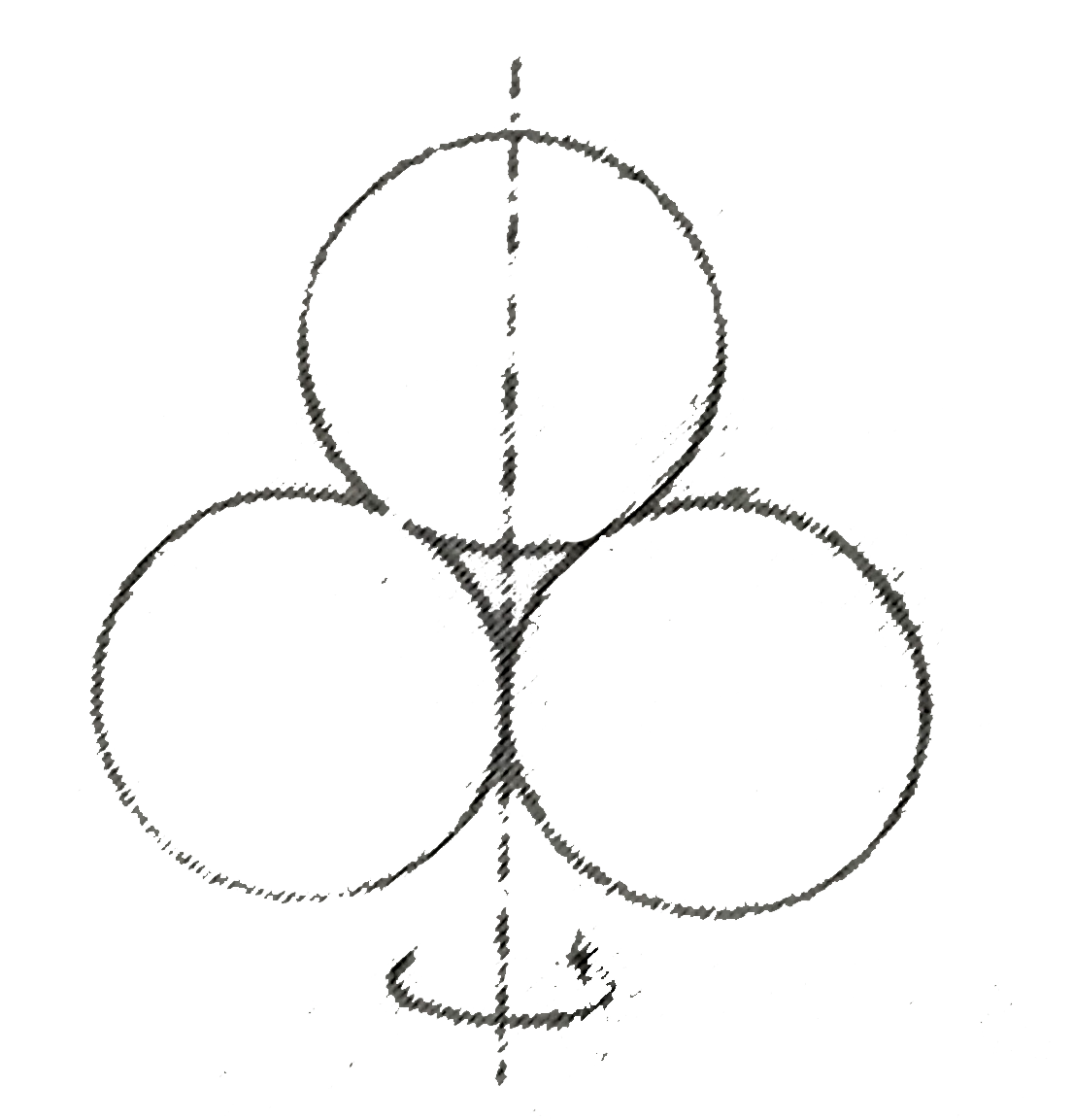 A√65rB√56rC√67rD√76r
A√65rB√56rC√67rD√76r

Find the moment of inertia of a solid sphere of mass M and radias R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
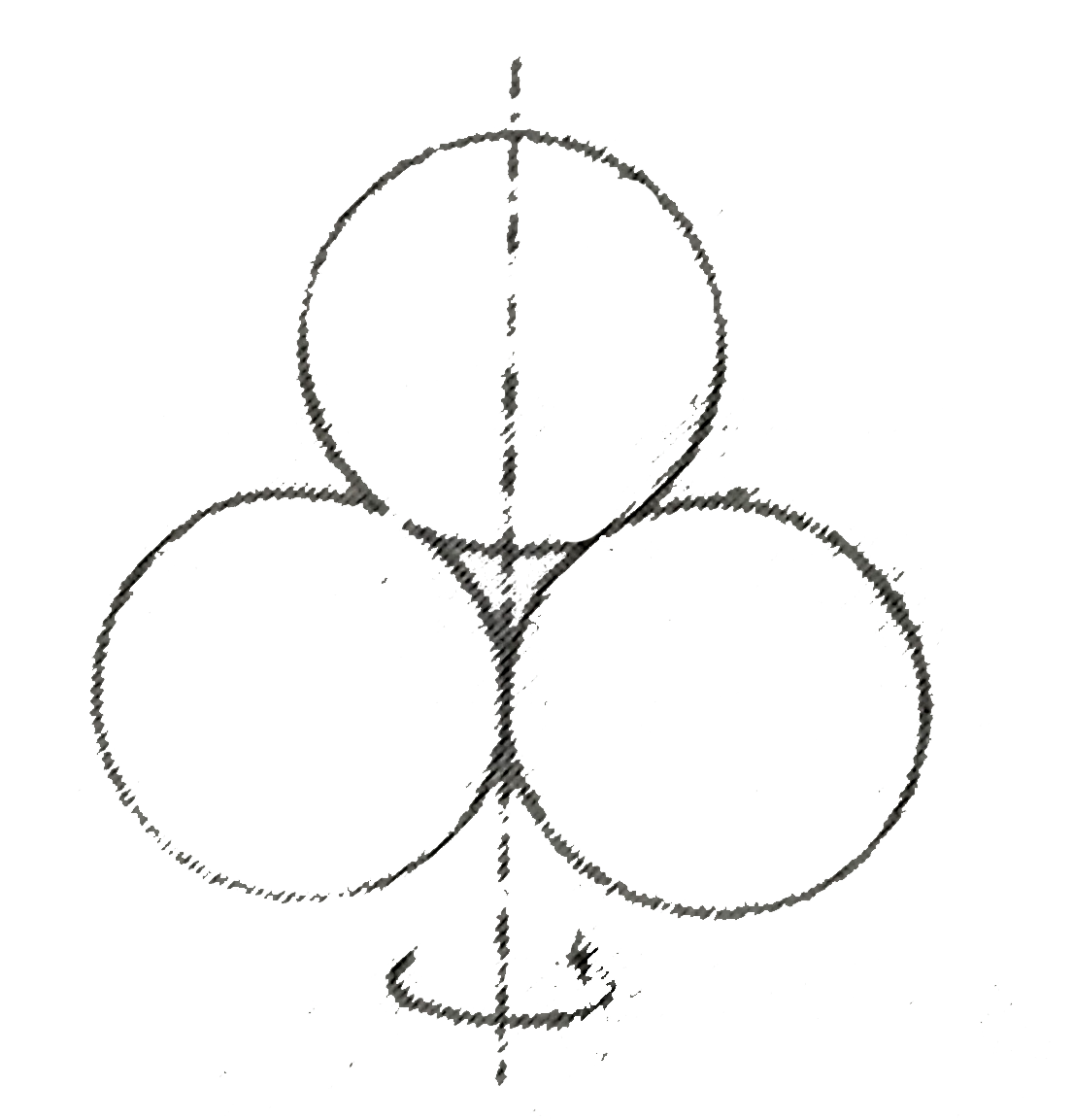
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system about an axis perpendicular to the plane of square and passing through its centre is
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis passing through opposite corners of frame is
View Solution
