
Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure. Also find radius of gyration about the given axis.
From theorem of parallel axes, the moment of inertia of solid sphere of mass is
. 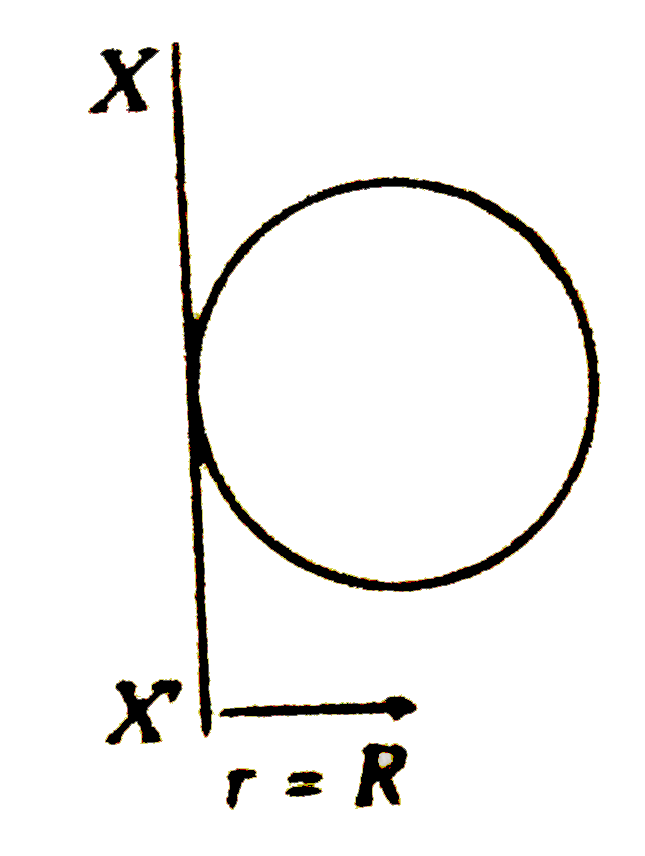
IXX'=ICM+MR2
=25MR2+MR2=75MR2=75(5)(2)2=28kg-m2.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
The moment of inertia of a hoop of radius R and mass M, about any tangent
A[3mR2]/2B[mR2]/2CMR2D[MR2]/4
Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
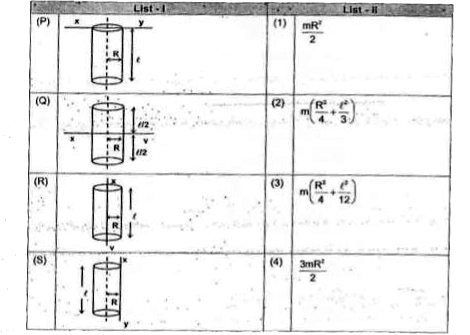
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution

