Four particles each having a charge q, are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is a. Find the electric field at the centre of the pentagon.
To find the electric field at the center of a regular pentagon with four charges placed at its vertices, we can follow these steps:
Step 1: Understand the Configuration
We have a regular pentagon with four charges q located at its vertices. The distance from the center of the pentagon to each vertex is given as a.
Step 2: Electric Field Due to a Single Charge
The electric field E due to a single charge q at a distance a from the charge is given by the formula:
E=kqa2
where k is Coulomb's constant.
Step 3: Determine the Direction of Electric Fields
Since we have four charges, we need to consider the direction of the electric field produced by each charge at the center of the pentagon. The electric field due to each charge will point away from the charge if the charge is positive.
Step 4: Symmetry Consideration
Due to the symmetry of the regular pentagon, the electric fields produced by the charges at the vertices will have components that cancel out. Specifically, for every charge, there is another charge that produces an electric field in the opposite direction.
Step 5: Calculate the Net Electric Field
Since the configuration is symmetric, the net electric field at the center of the pentagon due to the four charges will be zero. This can be expressed mathematically as:
Enet=E1+E2+E3+E4=0
where E1,E2,E3, and E4 are the electric fields due to each of the four charges.
Conclusion
Thus, the electric field at the center of the pentagon is:
Enet=0
We have a regular pentagon with four charges q located at its vertices. The distance from the center of the pentagon to each vertex is given as a.
The electric field E due to a single charge q at a distance a from the charge is given by the formula:
E=kqa2
where k is Coulomb's constant.
Since we have four charges, we need to consider the direction of the electric field produced by each charge at the center of the pentagon. The electric field due to each charge will point away from the charge if the charge is positive.
Due to the symmetry of the regular pentagon, the electric fields produced by the charges at the vertices will have components that cancel out. Specifically, for every charge, there is another charge that produces an electric field in the opposite direction.
Since the configuration is symmetric, the net electric field at the center of the pentagon due to the four charges will be zero. This can be expressed mathematically as:
Enet=E1+E2+E3+E4=0
where E1,E2,E3, and E4 are the electric fields due to each of the four charges.
Thus, the electric field at the center of the pentagon is:
Enet=0
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
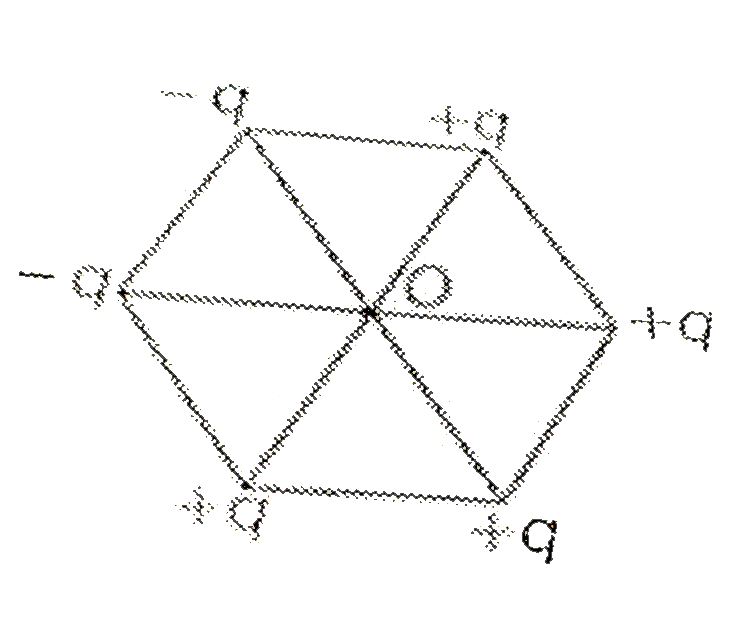
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
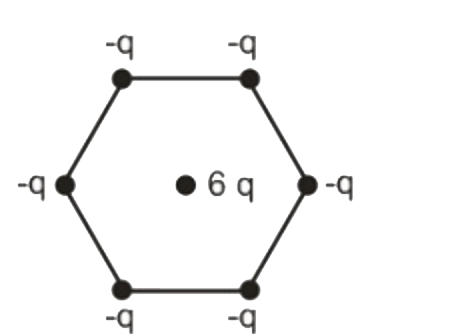
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
View SolutionProve that the any four vertices of a regular pentagon are concyclic (lie on the same circle).
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
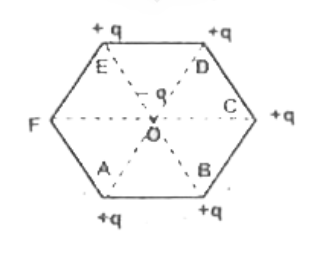
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View SolutionShow that any four vertices of a regular pentagon form a cyclic quadrilateral.
View Solution
