Four particles, each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is

A

$\frac{G M}{R}$

B

$\sqrt{2 \sqrt{2} \frac{G M}{R}}$

C

$\sqrt{\frac{G M}{R} (2 \sqrt{2} + 1)}$

D

$\sqrt{\frac{G M}{R} (\frac{2 \sqrt{2} + 1}{4})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$F_{12} = \frac{G M^{2}}{2 R^{2}}$
$F_{14} = \frac{G M^{2}}{2 R^{2}}$

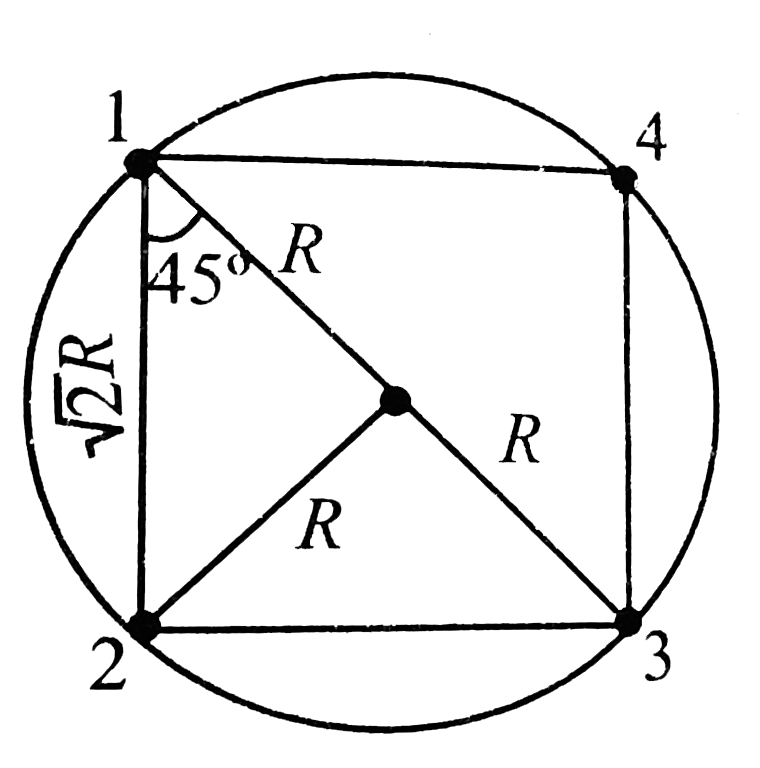
The resultant of these two forces is $(\sqrt{2} G M^{2}) / 2 R^{2})$ . Now $F_{12} (G M^{2}) / (4 R^{2})$ .
The combined resultant of all the forces is
$\frac{\sqrt{2} G M^{2}}{2 R^{2}} + \frac{G M^{2}}{4 R^{2}}$ or $\frac{G M^{2}}{4 R^{2}} [\frac{\sqrt{2}}{2} + \frac{1}{4}]$
Equating this with centripetal force, we get
$\frac{M v^{2}}{R} = \frac{G M^{2}}{R} [\frac{2 \sqrt{2} + 1}{4}]$
or $v^{2} = \frac{G M}{R} [\frac{2 \sqrt{2} + 1}{4}]$ or $v = \sqrt{\frac{G M}{R} (\frac{2 \sqrt{2} + 1}{4})}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A $\frac{1}{2 R} \sqrt{(\frac{1}{G m})}$
B $\sqrt{(\frac{G m}{2 R})}$
C $\frac{1}{2} \sqrt{(\frac{G m}{R})}$
D $\sqrt{(\frac{4 G m}{R})}$

CENGAGE PHYSICS ENGLISH-GRAVITATION-Single Correct

Home
Ask Doubt
Profile