Four point masses P, Q, R and S with respective masses 1 kg, 1 kg, 2 kg and 2 kg form the corners of a square of side a. The centre of mass of the system will be farthest from
R and S
R only
P and Q
P and R
The correct Answer is:C
To solve the problem of finding the center of mass of the four point masses arranged at the corners of a square, we will follow these steps:
Step 1: Define the coordinates of the masses
Let's place the square in a Cartesian coordinate system. We can define the positions of the masses as follows:
- Mass P (1 kg) at (a/2, a/2)
- Mass Q (1 kg) at (a/2, -a/2)
- Mass R (2 kg) at (-a/2, a/2)
- Mass S (2 kg) at (-a/2, -a/2)
Step 2: Calculate the total mass
The total mass M of the system is the sum of all the individual masses:
M=mP+mQ+mR+mS=1kg+1kg+2kg+2kg=6kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is given by the formula:
xcm=1M∑mixi
Substituting the values:
xcm=16(1⋅a2+1⋅a2+2⋅(−a2)+2⋅(−a2))
Calculating this:
xcm=16(a2+a2−a−a)=16(a2+a2−2a)=16(a−2a)=16(−a)=−a6
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is given by:
ycm=1M∑miyi
Substituting the values:
ycm=16(1⋅a2+1⋅(−a2)+2⋅a2+2⋅(−a2))
Calculating this:
ycm=16(a2−a2+a−a)=16(0)=0
Step 5: Determine the position of the center of mass
The center of mass is located at:
(−a6,0)
This means the center of mass is on the negative x-axis.
Step 6: Identify which mass is farthest from the center of mass
Since the center of mass is located at (−a6,0), we can analyze the distances from the center of mass to each mass:
- Distance to P: √(a2+a6)2+(a2)2
- Distance to Q: √(a2+a6)2+(−a2)2
- Distance to R: √(−a2+a6)2+(a2)2
- Distance to S: √(−a2+a6)2+(−a2)2
After calculating these distances, we find that the distances to P and Q are greater than those to R and S.
Conclusion
The center of mass is farthest from points P and Q.
Let's place the square in a Cartesian coordinate system. We can define the positions of the masses as follows:
- Mass P (1 kg) at (a/2, a/2)
- Mass Q (1 kg) at (a/2, -a/2)
- Mass R (2 kg) at (-a/2, a/2)
- Mass S (2 kg) at (-a/2, -a/2)
The total mass M of the system is the sum of all the individual masses:
M=mP+mQ+mR+mS=1kg+1kg+2kg+2kg=6kg
The x-coordinate of the center of mass xcm is given by the formula:
xcm=1M∑mixi
Substituting the values:
xcm=16(1⋅a2+1⋅a2+2⋅(−a2)+2⋅(−a2))
Calculating this:
xcm=16(a2+a2−a−a)=16(a2+a2−2a)=16(a−2a)=16(−a)=−a6
The y-coordinate of the center of mass ycm is given by:
ycm=1M∑miyi
Substituting the values:
ycm=16(1⋅a2+1⋅(−a2)+2⋅a2+2⋅(−a2))
Calculating this:
ycm=16(a2−a2+a−a)=16(0)=0
The center of mass is located at:
(−a6,0)
This means the center of mass is on the negative x-axis.
Since the center of mass is located at (−a6,0), we can analyze the distances from the center of mass to each mass:
- Distance to P: √(a2+a6)2+(a2)2
- Distance to Q: √(a2+a6)2+(−a2)2
- Distance to R: √(−a2+a6)2+(a2)2
- Distance to S: √(−a2+a6)2+(−a2)2
The center of mass is farthest from points P and Q.
Topper's Solved these Questions
Similar Questions
Particle of masses 2 kg, 2 kg, 1 kg and 1 kg are placed at the corners A, B, C, D of a square of side L as shown in Fig. Find the centre of mass of the system.

View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View Solution
Knowledge Check
Four bodies of masses 2, 3, 5 and 8 kg are placed at the four corners of a square of side 2 m. The position of CM will be -
A(89,139)B(79,119)C(119,139)D(119,89)Four particles of masses 1kg,2kg,3kg and 4kg are placed at the corners of a square of side 2m in the x-y plane If the origin of the co-ordinate system is taken at the mass of 1kg, the (x,y) co-ordinates of the enter of mass expressed in metre are :
A(1,75)B(2,75)C(3,75)D(4,75)Four particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
A(0.5,0.3)B(0.4,0.3)C(0.5,0.8)D(0.7,0.3)
Four particles of mass 2 kg, 3kg, 4 kg and 8 kg are situated at the comers of a square of side length 2 m. The centre of mass may be given as
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionFour particles of masses 1 kg, 2 kg, 3 kg, 4 kg are placed at the corners of a square of side 2 m. Find the coordinates of centre of mass.
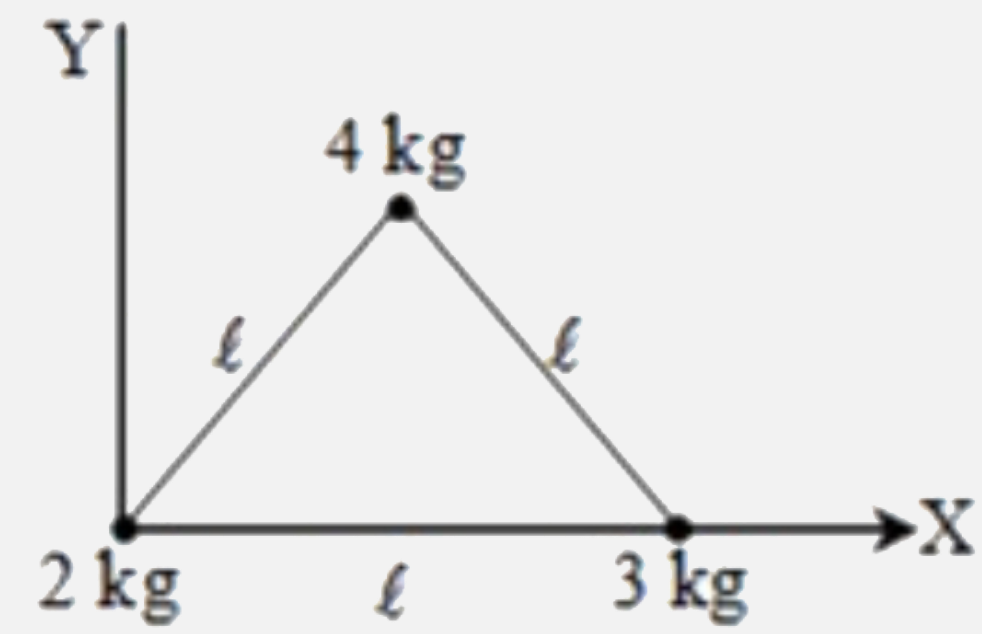
View SolutionThree masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
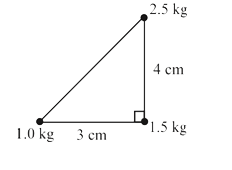
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
View Solution
