Four particles of mass 2 kg, 3kg, 4 kg and 8 kg are situated at the comers of a square of side length 2 m. The centre of mass may be given as
(3018,2818)
(frac(20sqrt)(18),frac(24sqrt2)(18))
(1417,2417)
(3418,3418)
To find the center of mass of the four particles situated at the corners of a square, we will follow these steps:
Step 1: Identify the coordinates of the particles
We have four particles with the following masses and coordinates:
- Particle 1 (mass = 2 kg) at (0, 0)
- Particle 2 (mass = 3 kg) at (2, 0)
- Particle 3 (mass = 4 kg) at (2, 2)
- Particle 4 (mass = 8 kg) at (0, 2)
Step 2: Calculate the total mass
The total mass M of the system is the sum of all individual masses:
M=m1+m2+m3+m4=2+3+4+8=17 kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is given by the formula:
xcm=∑mixiM
Substituting the values:
xcm=(2×0)+(3×2)+(4×2)+(8×0)17
Calculating the numerator:
=0+6+8+017=1417
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is given by the formula:
ycm=∑miyiM
Substituting the values:
ycm=(2×0)+(3×0)+(4×2)+(8×2)17
Calculating the numerator:
=0+0+8+1617=2417
Step 5: Write the final coordinates of the center of mass
Thus, the coordinates of the center of mass are:
(1417,2417)
Final Answer
The center of mass of the system is at the point (1417,2417).
---
We have four particles with the following masses and coordinates:
- Particle 1 (mass = 2 kg) at (0, 0)
- Particle 2 (mass = 3 kg) at (2, 0)
- Particle 3 (mass = 4 kg) at (2, 2)
- Particle 4 (mass = 8 kg) at (0, 2)
The total mass M of the system is the sum of all individual masses:
M=m1+m2+m3+m4=2+3+4+8=17 kg
The x-coordinate of the center of mass xcm is given by the formula:
xcm=∑mixiM
Substituting the values:
xcm=(2×0)+(3×2)+(4×2)+(8×0)17
Calculating the numerator:
=0+6+8+017=1417
The y-coordinate of the center of mass ycm is given by the formula:
ycm=∑miyiM
Substituting the values:
ycm=(2×0)+(3×0)+(4×2)+(8×2)17
Calculating the numerator:
=0+0+8+1617=2417
Thus, the coordinates of the center of mass are:
(1417,2417)
The center of mass of the system is at the point (1417,2417).
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Four particles of masses 1 kg, 2 kg, 3 kg, 4 kg are placed at the corners of a square of side 2 m. Find the coordinates of centre of mass.
View SolutionFour particles of masses 2 kg, 3 kg, 2 kg and 4 kg are at the corners of a square of diagonal 4 m, as shown. The net gravitational force on a particle of mass 1 kg at the centre of the square is [Take G=203×10−11 SI units, pN≡piconewton]

View Solution
Knowledge Check
Four bodies of masses 2, 3, 5 and 8 kg are placed at the four corners of a square of side 2 m. The position of CM will be -
A(89,139)B(79,119)C(119,139)D(119,89)Four particles of masses 1kg,2kg,3kg and 4kg are placed at the corners of a square of side 2m in the x-y plane If the origin of the co-ordinate system is taken at the mass of 1kg, the (x,y) co-ordinates of the enter of mass expressed in metre are :
A(1,75)B(2,75)C(3,75)D(4,75)Three particles of masses 1 kg, 2 kg and 3 kg are situated at the corners of an equilateral triangle of side b in the x-y plane with mass 1 kg at the origin and 2 kg on the x-axis. The coordinates of the centre of mass are
A(7b12,3√3b12)B(3√3b12,7b12)C(b12,3√3b12)D(7b12,√3b12)
Particle of masses 2 kg, 2 kg, 1 kg and 1 kg are placed at the corners A, B, C, D of a square of side L as shown in Fig. Find the centre of mass of the system.

View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionFour particles of masses 1 kg, 2 kg, 3 kg, and 4 kg are situated at the corners of a square and moving at speed 3ms−1,4ms−1,1ms−1 and 2ms−1 respectively. Each particle maintains a direction towards the particle at the next comer symmetrically. The momentum of the system at this instant is
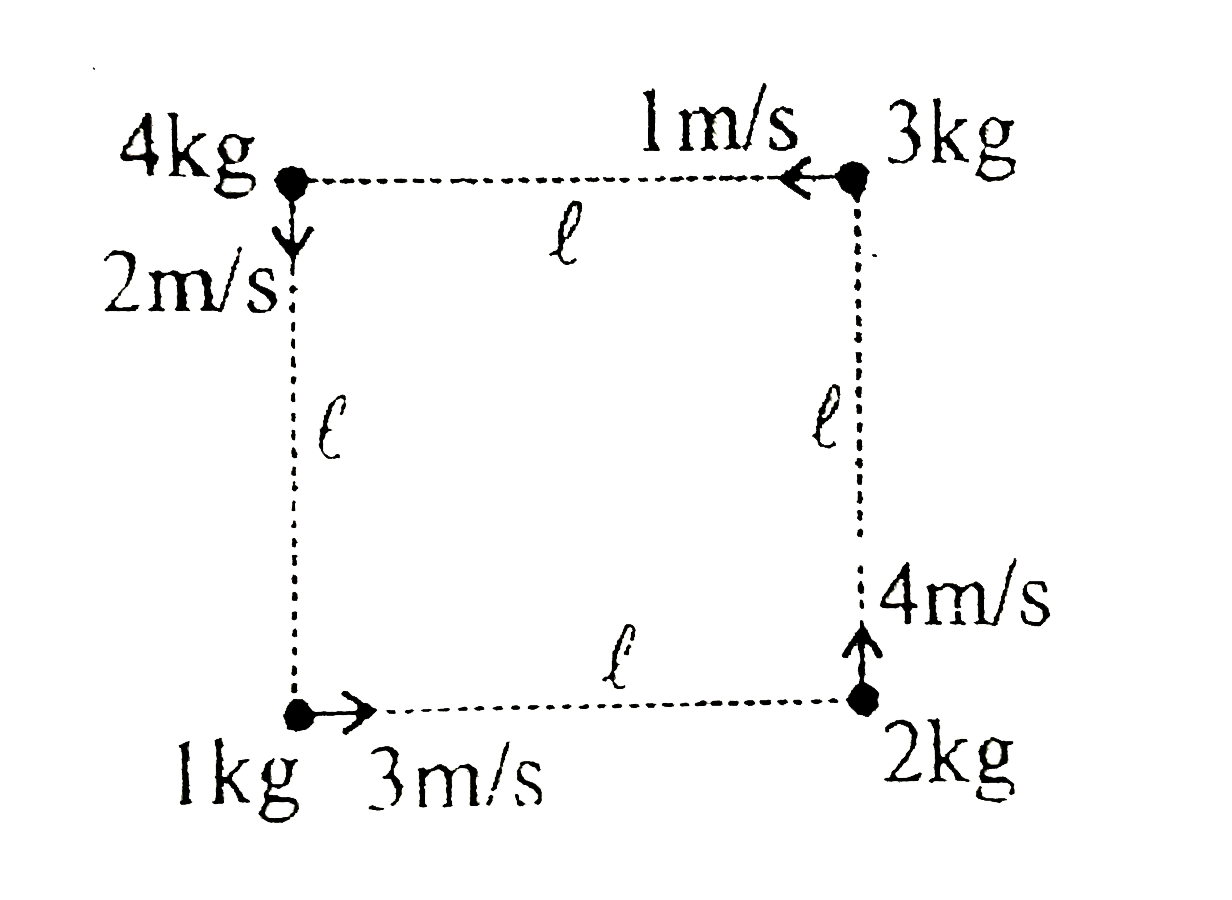
View SolutionFour bodies of masses 1,2,3,4kg respectively are placed at the comers of a square of side a. Coordinates of centre of mass are (take 1kg at the origin,2kg on X-axis and 4kg on Y-axis)
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View Solution
