Four resistances, each of 10Ω, are connected to form a square as shown in (Fig. 3.52), find the equivalent resistance between the opposite corners AandC.
 .
.
Resistance in the path ADC=10Ω+10Ω=20Ω
Resistance in the path ABC=10Ω+10Ω=20Ω
Since the resistances in the paths ADC and ABC are in parallel. Resistance between A and C, i.e.,
1R=120+120=220=110 or R=10Ω.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Higher Order Thinking7videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Value Based Question4videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Additional)Long Answer4videos
ELECTRICITY
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test21videos
MAGNETIC EFFECTS OF ELECTRIC CURRENT
Similar Questions
Four resistances, each of 10Ω, are connected to form a square as shown in (Fig. 3.52), find the equivalent resistance between two points on any one side (AB).
 .View Solution
.View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
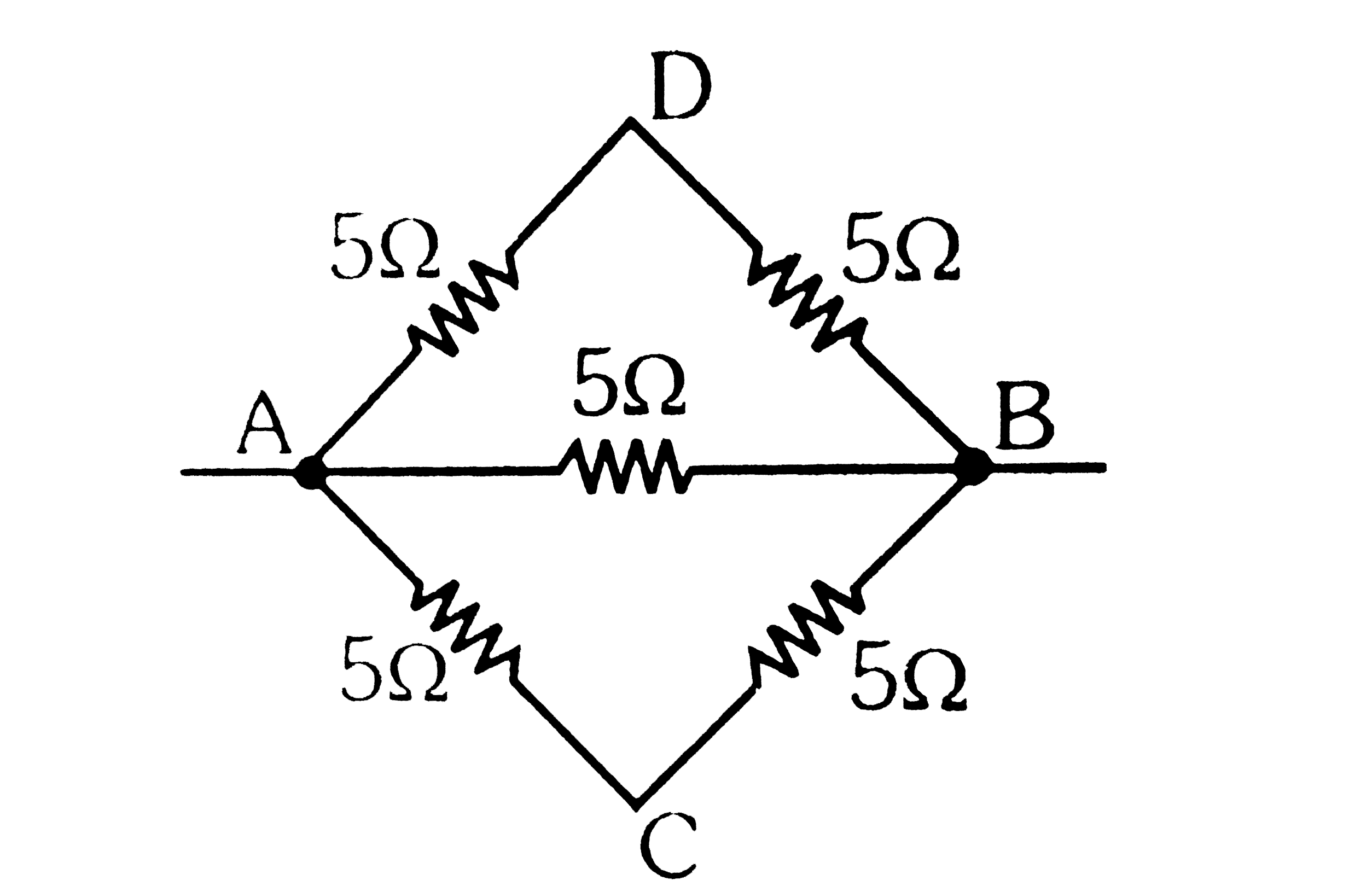 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω - Question 2 - Select One
Eight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
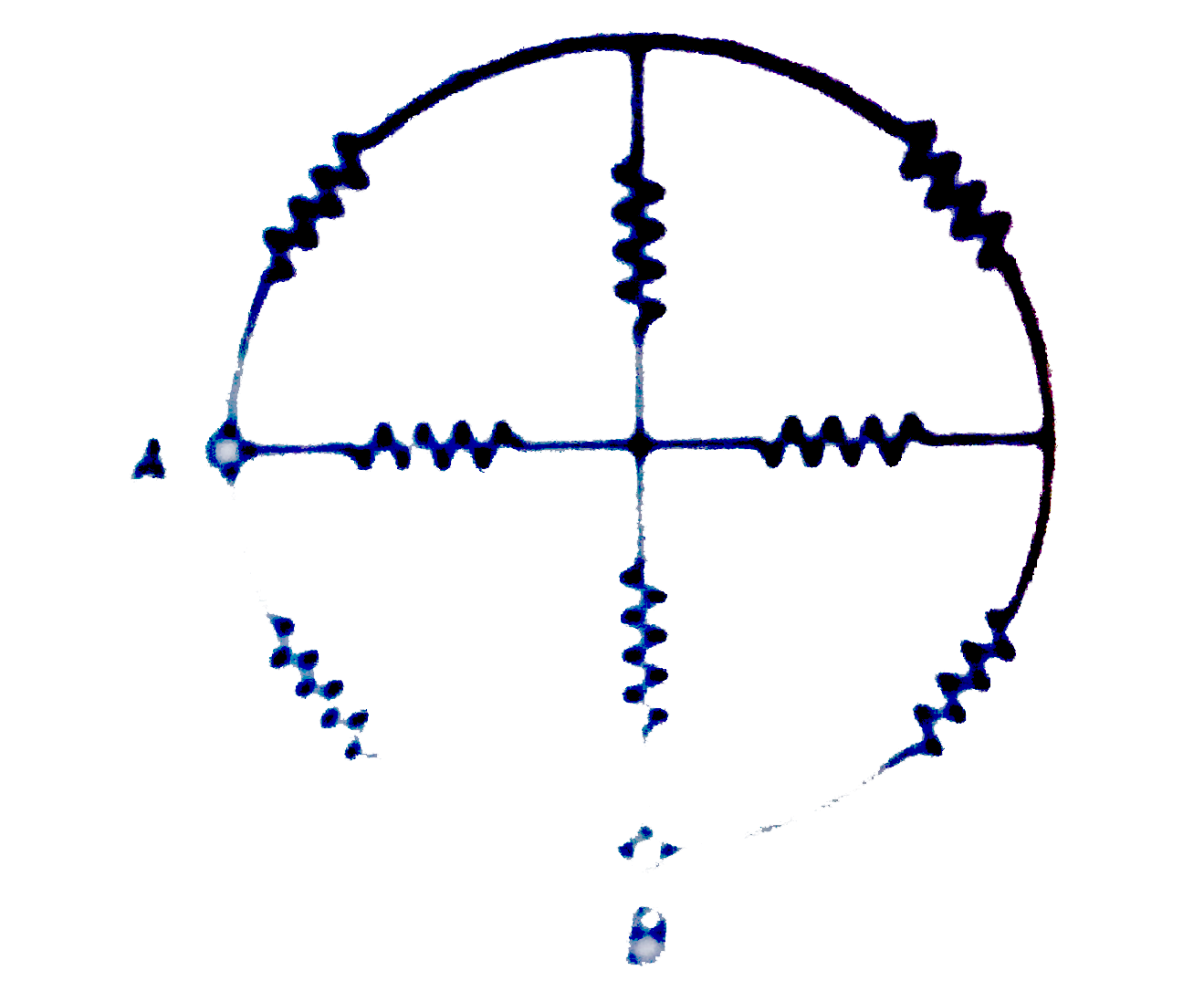 A83ΩB163ΩC157ΩD192Ω
A83ΩB163ΩC157ΩD192Ω - Question 3 - Select One
Six equal resistances, each 1Ω, are joined to form a network as shown in fig. Then the resistance between any two corners is
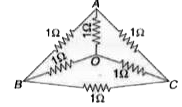 A0.5ΩB2ΩC1ΩD1.5Ω
A0.5ΩB2ΩC1ΩD1.5Ω

Eight identical resistance each 15Ω are connected along the edge of a pyramid having square base as shown. Find the equivalent resistance between A and D in ΩView SolutionFive resistance are connected as shown in the figure. The equivalent resistance between points A and C is
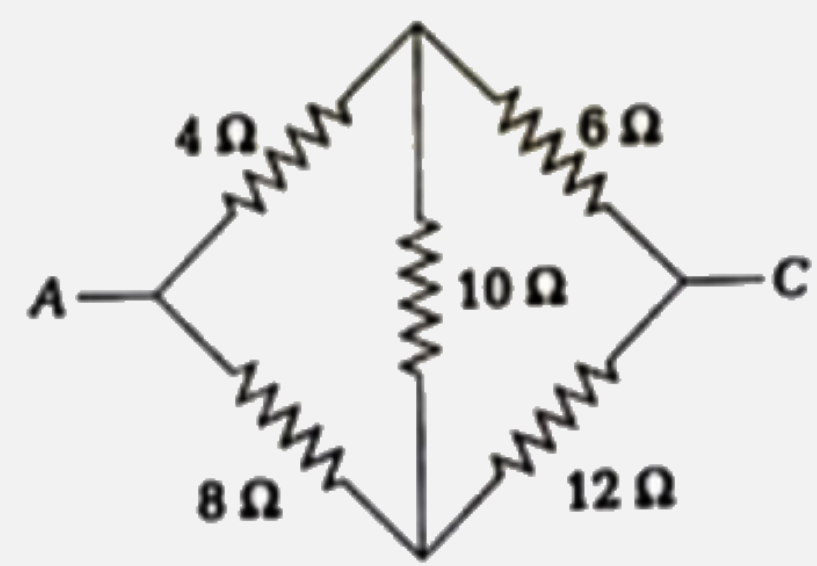 View Solution
View SolutionFor the circuit shown in fig. the equivalent resistance between A and C is
 View Solution
View SolutionSix equal resistances, each 1Ω, are joined to form a network as showing figure Then the resistance between any two corners is
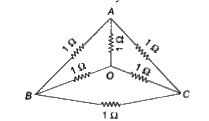 View Solution
View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View Solution

