Four resistances, each of 10Ω, are connected to form a square as shown in (Fig. 3.52), find the equivalent resistance between two points on any one side (AB).
 .
.
Video Solution
Text Solution
Resistance in the path ADCB=10Ω+10Ω+10Ω=30Ω
This resistance of 30Ω is in parallel with AB(=10Ω)
Equivalent resistance, i.e., 1R=130+110=1+330=430 or R=304=7.5Ω.
|
Topper's Solved these Questions
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Higher Order Thinking
7 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Value Based Question
4 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Additional)Long Answer
4 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test
21 Videos
Similar Questions
Knowledge Check
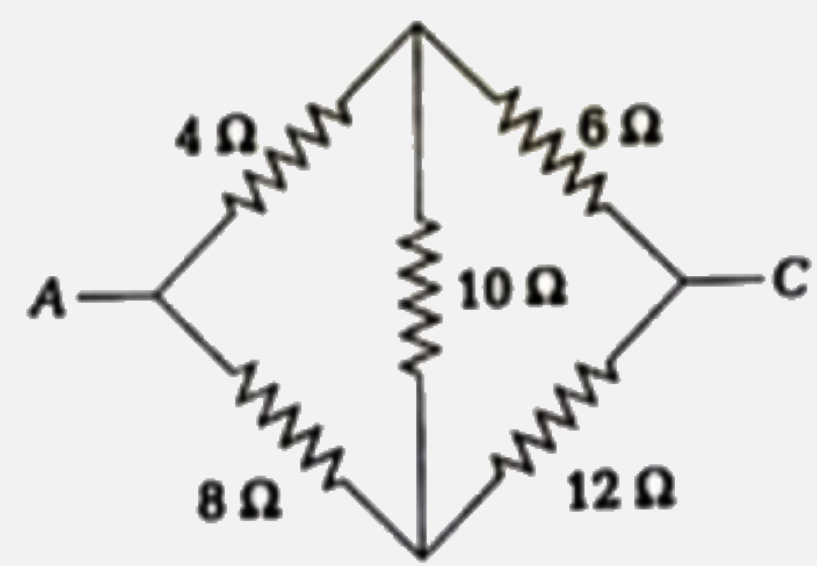
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
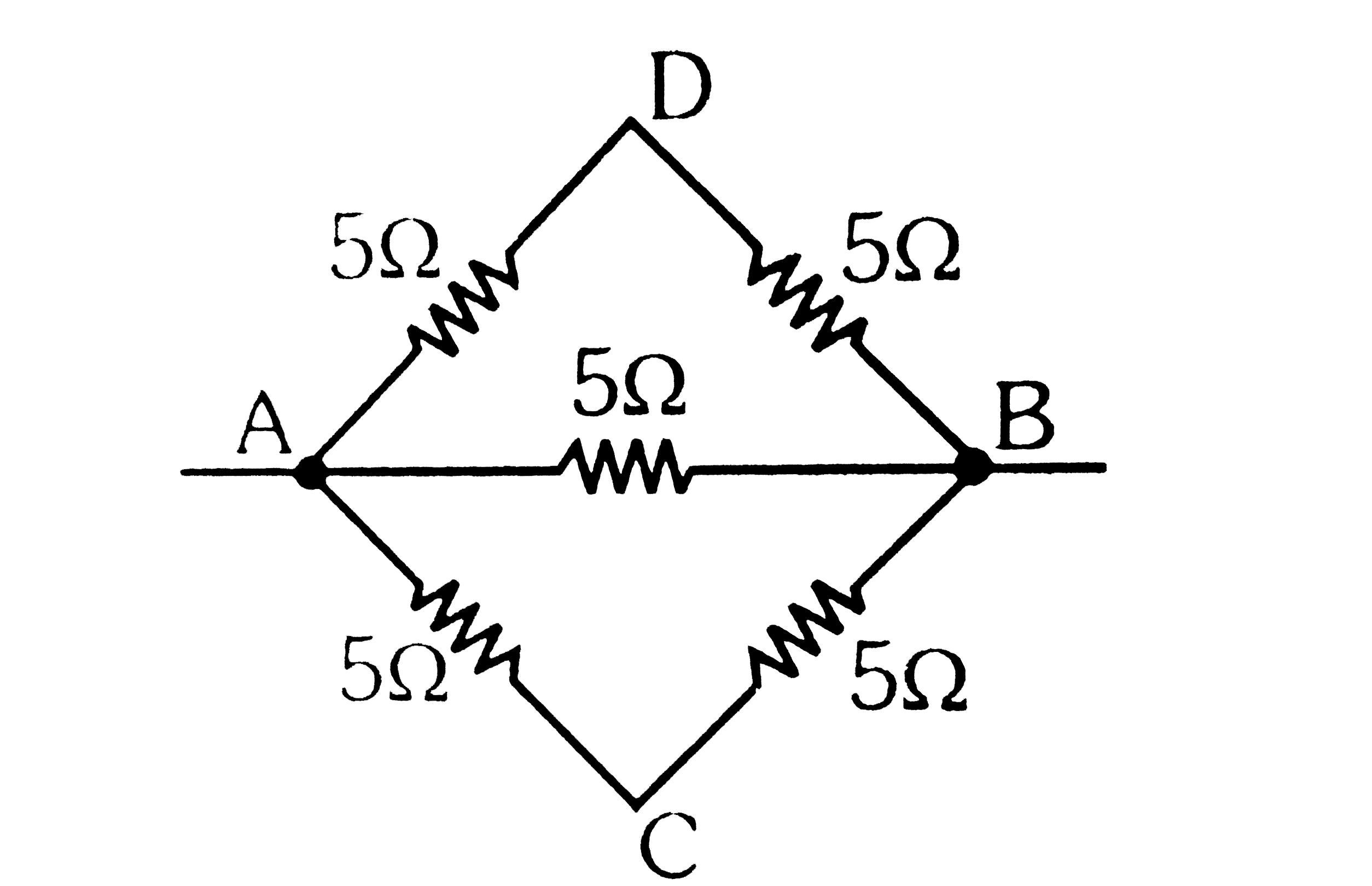
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5ΩEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
 A83ΩB163ΩC157ΩD192Ω
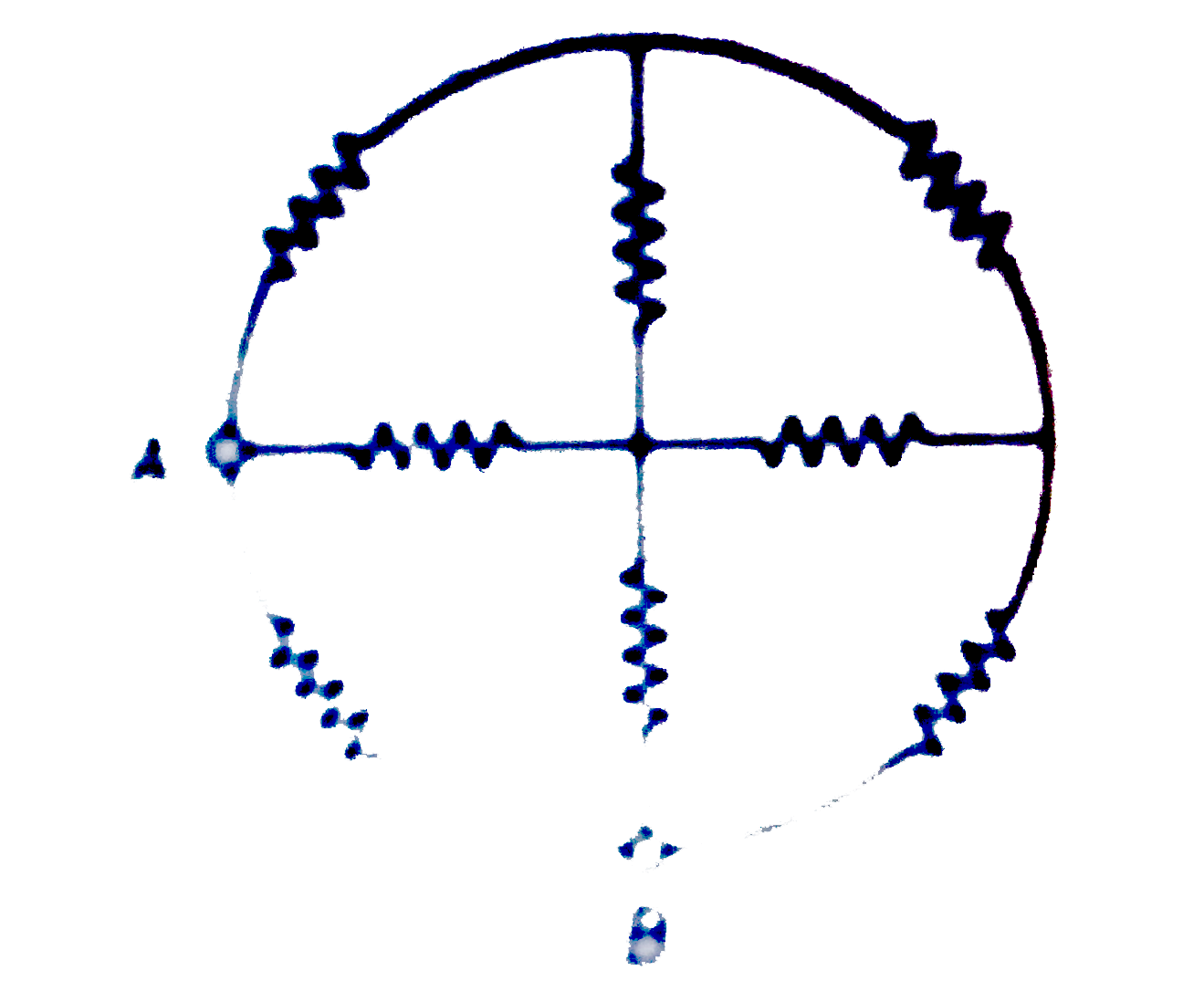
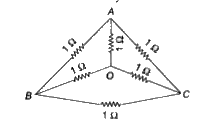
A83ΩB163ΩC157ΩD192ΩSix equal resistances, each 1Ω, are joined to form a network as shown in fig. Then the resistance between any two corners is
 A0.5ΩB2ΩC1ΩD1.5Ω
A0.5ΩB2ΩC1ΩD1.5Ω
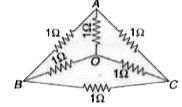
For the circuit shown in fig. the equivalent resistance between A and C is

View SolutionSix equal resistances, each 1Ω, are joined to form a network as showing figure Then the resistance between any two corners is
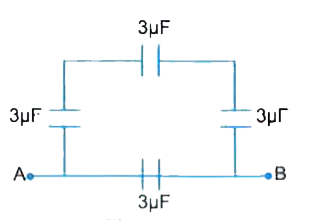
View SolutionFour capacitors are connected as shown in Fig. The equivalent capacitance between the points A and B is
View Solution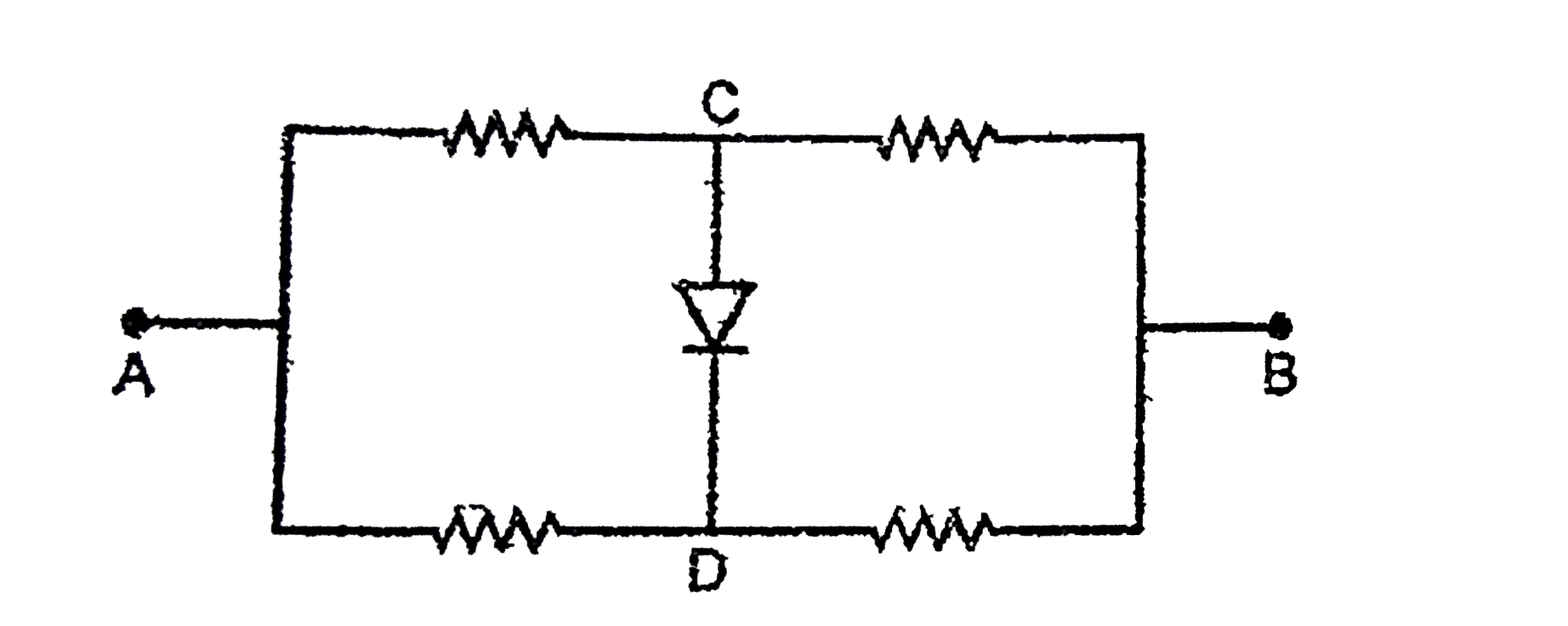
Four equal resistors, each of resistance 10 ohm are connected as shown in the adjoining circuit diagram. Then the equivalent resistance between points A and B is-
View SolutionEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
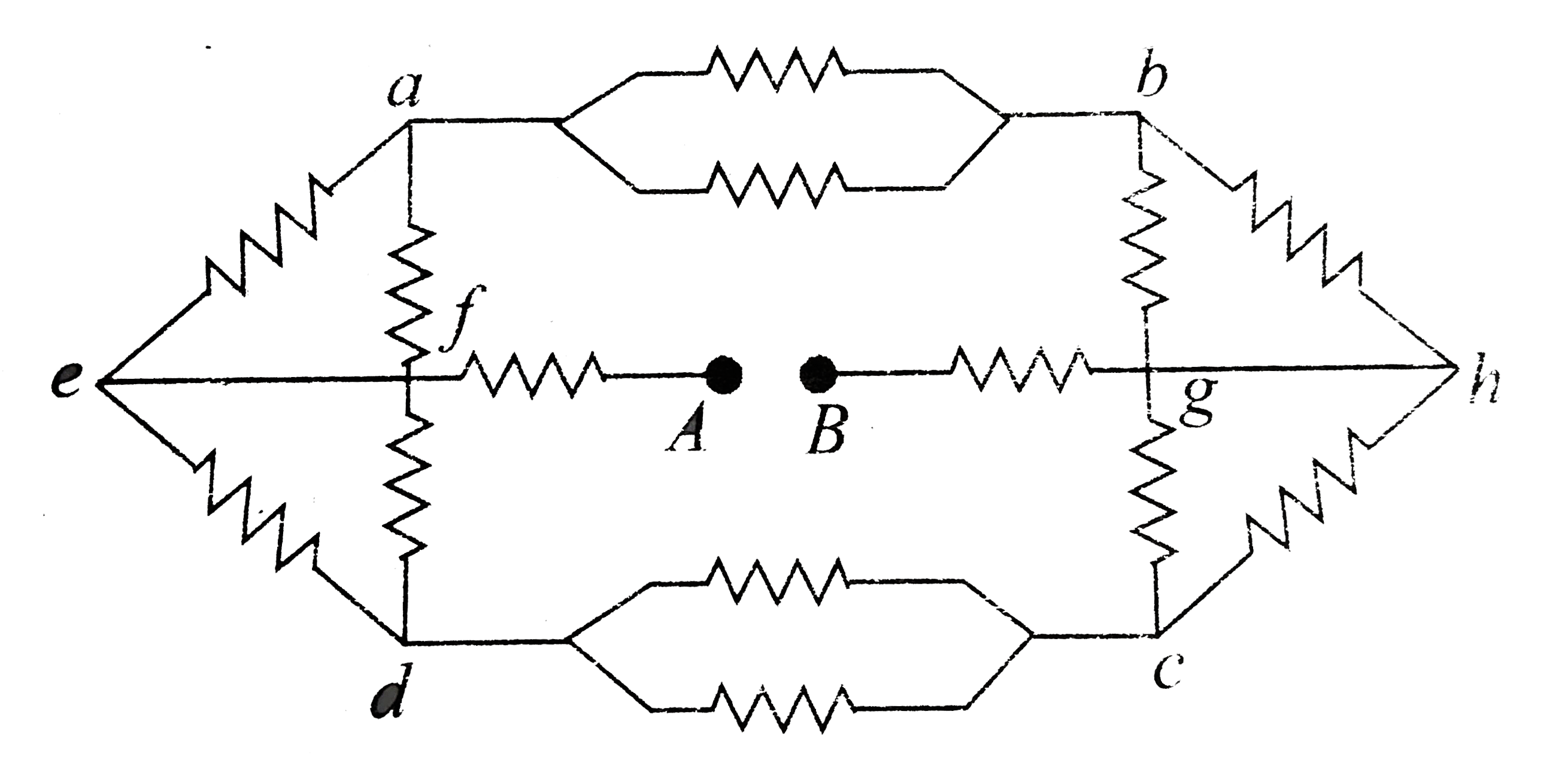
View Solution

 .
.