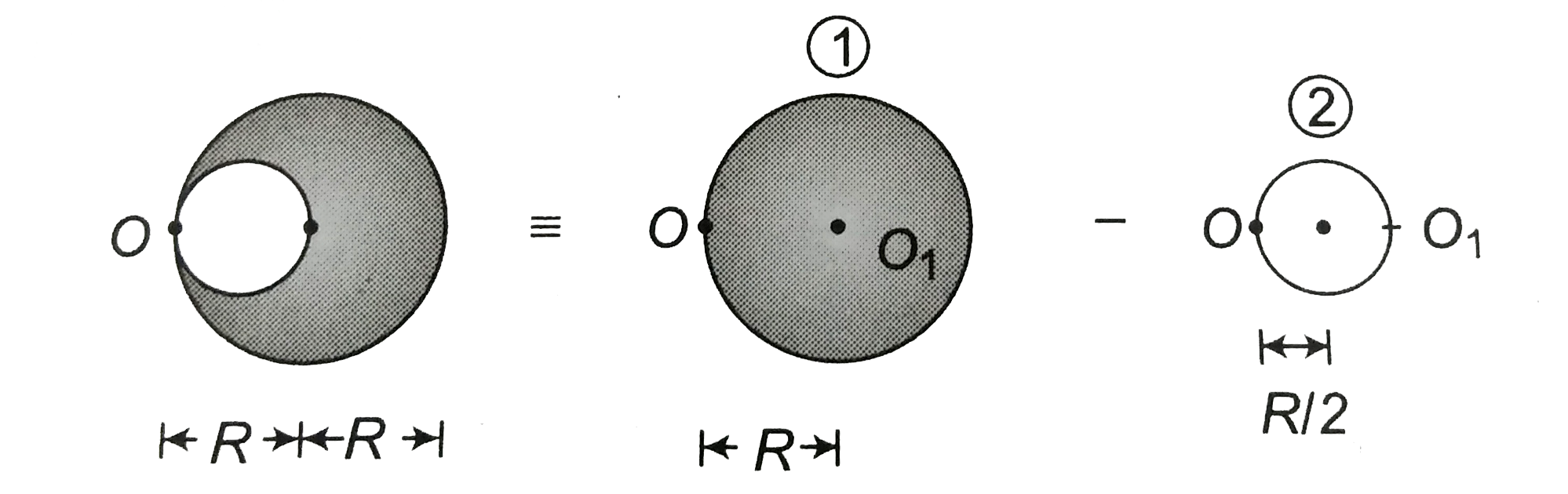
From a circular disc of radius R, another disc of diameter R is removed. Locate c.m. of the remaining portion.

Here , from the larger disc, smaller disc is removed.
Larger disc : m1∝πR2⇒m1=m,x1=R
m2∝π(R/2)2⇒m2=m4,x2=R2
c.m of the remaining position
xc.m.=m1x1−m2x2m1−m2=mR−m4×R2m−m4=7mR83m4=7R6
Topper's Solved these Questions
Similar Questions
From a thin uniform disc of radius 2R. Another disc of diameter 2R is removed. The mass of the remaining portion is m. Find the M.I. of the shaded portion about an axis passing through O and pependicular to the plane.
View SolutionFrom a disc of radius r1, a concentric disc of radius r2 is removed . The mass of the remaining portion is m. Find the M.I. of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View Solution
Knowledge Check
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
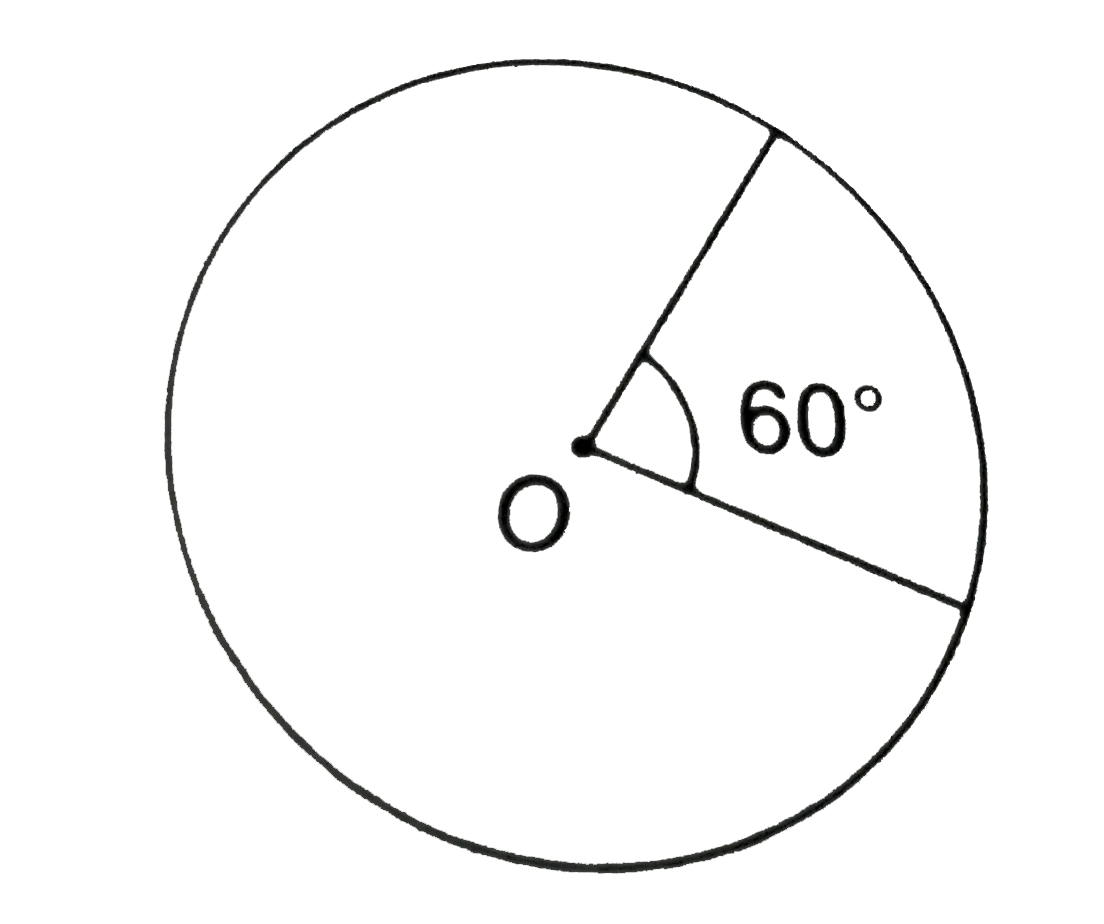 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
A(M−m)(R+r)2/2B(M−m)(R2−r2)/2C(M−m)(R−r)2/2D(M−m)(R2+r2)/2From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
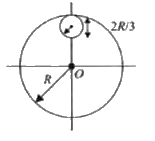 A4M2B409MR2C10MR2D379MR2
A4M2B409MR2C10MR2D379MR2
From a semicircular disc of radius r1, another semicircular disc of radius r2 is removed. Find the c.m. of the remaining position.

View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use π=22/7 and √149=12.2)
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View Solution
