From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
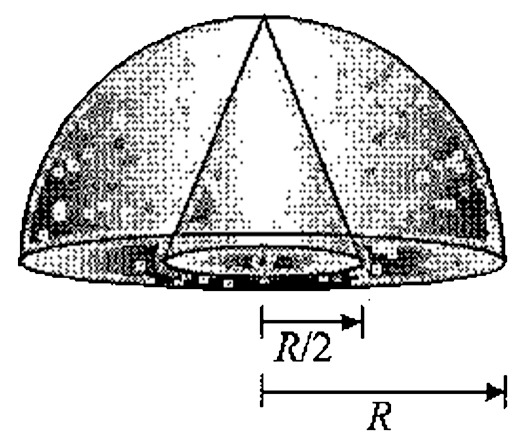
Step by step video & image solution for From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Conceptual MCQ s single option correct
30 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is

View SolutionA disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View Solution
Knowledge Check
A solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.
 AR2B3R8C7R8D9R8
AR2B3R8C7R8D9R8A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20From a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :
 A(0,0)B(0,R)C(0,√3R2)Dnone of these
A(0,0)B(0,R)C(0,√3R2)Dnone of these
The curved surface area of a cone of base radius r and height h is_______.
View SolutionA solid hemisphere of radius R is mounted on a solid cylinder of same radius and density as shown .the height of cylinder is such that the resulting centre of mass is at O. if radius of sphrere is 2√2m, what is the height of the cylinder (in m ) ?
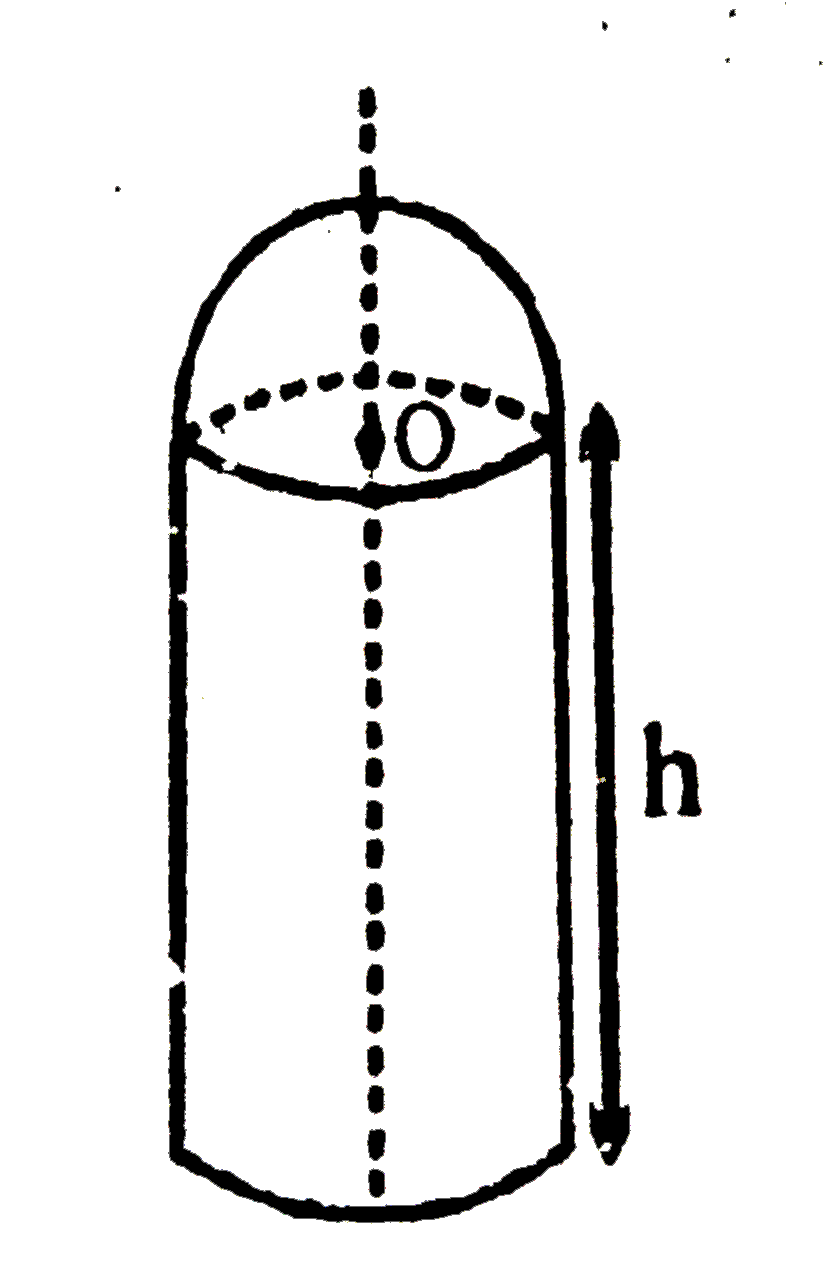
View SolutionA hemispherical sheli of mass M and radius R made to vibrate as shown in figure. Find its frequency of oscillation.

View SolutionA sphere of radius r has the same volume as that of a cone with a circular base of radius r. Find the height of the cone.
View SolutionA uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is

View Solution
