The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
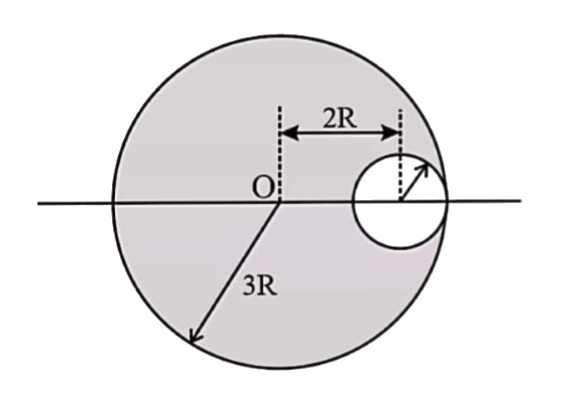
R/4
R/5
R/3
R/6
Step by step video & image solution for The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
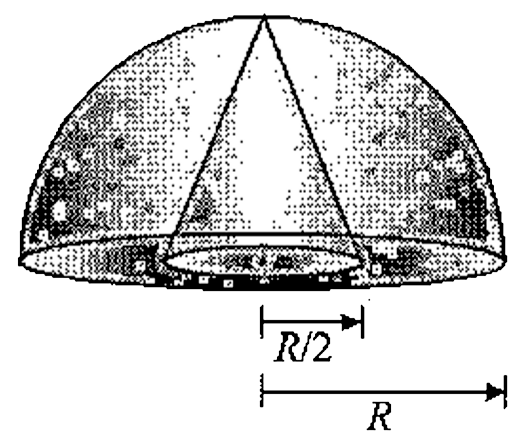
From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
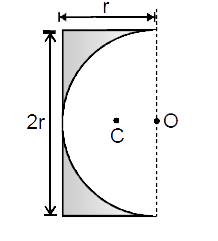
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
View Solution
Knowledge Check
From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
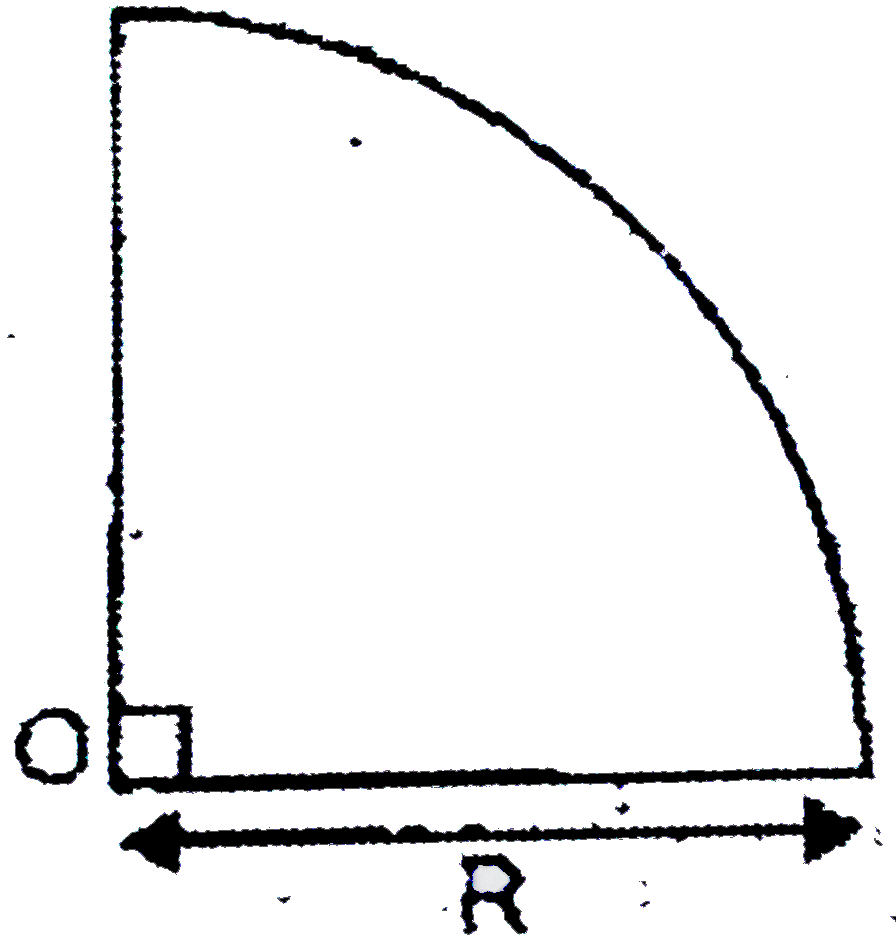 A4R3πB2r3πC√24R3πD√22R3π
A4R3πB2r3πC√24R3πD√22R3π
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
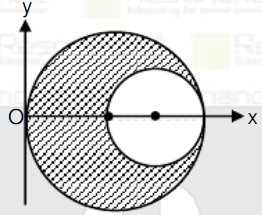
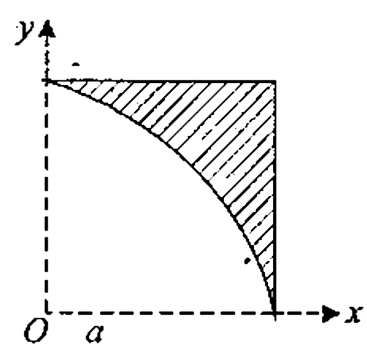
View SolutionFron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.
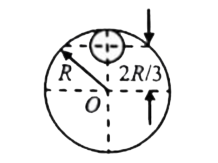
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View Solution
