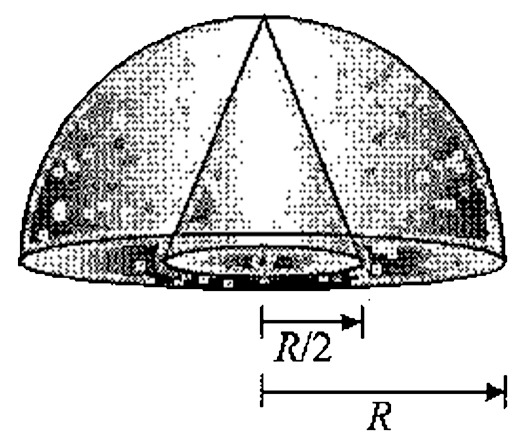
From a solid sphere a small part A is cut by a plane at a distance R/2 from the centre as shown in figure-4.32. Find the centre of mass of object A.

Step by step video & image solution for From a solid sphere a small part A is cut by a plane at a distance R//2 from the centre as shown in figure-4.32. Find the centre of mass of object A. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
From a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
View SolutionA solid sphere of mass m and radius r initially placed at a distance 5r from the centre of a point mass M as shown in figure. Now During displacement, it is also uniformly expanded to a radius 2 r so that its density decreases uniformly throughout its volume. Find the work required in this process.

View Solution
Knowledge Check
The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0RA sphere of radius 5 cm is cut by a plane at a distance of 4 cm from its centre. Find the radius of circular section hence formed.
A3 cmB5 cmC4 cmD6 cmA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
Amg2B3mg8Cmg16Dnone of these
A uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View SolutionA circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionThere is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution
