From a solid sphere of mass M and radius R, a spherical portion of radiu is removed as shown in the figure. Taking gravitational potential V = 0 at , the potential at the centre of the cavity thus formed is (G = gravitational constant)
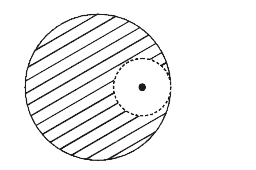
The correct Answer is:A
Mass of radius R is M
Mass of radius is
Potential at O. due to mass M (Due to entire solid sphere)

Potential at centre O. for mass M/8
Potential due to remaining mass of sphere at point O..
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( Jee (Advanced) for IIT Entrance)
6 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( C. Multiple Choice Questions)
12 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE (B.(Multipe Choice Questions from Competitive Examinations) AIPMT/NEET & Other State Boards for Medical Entrance)
16 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown
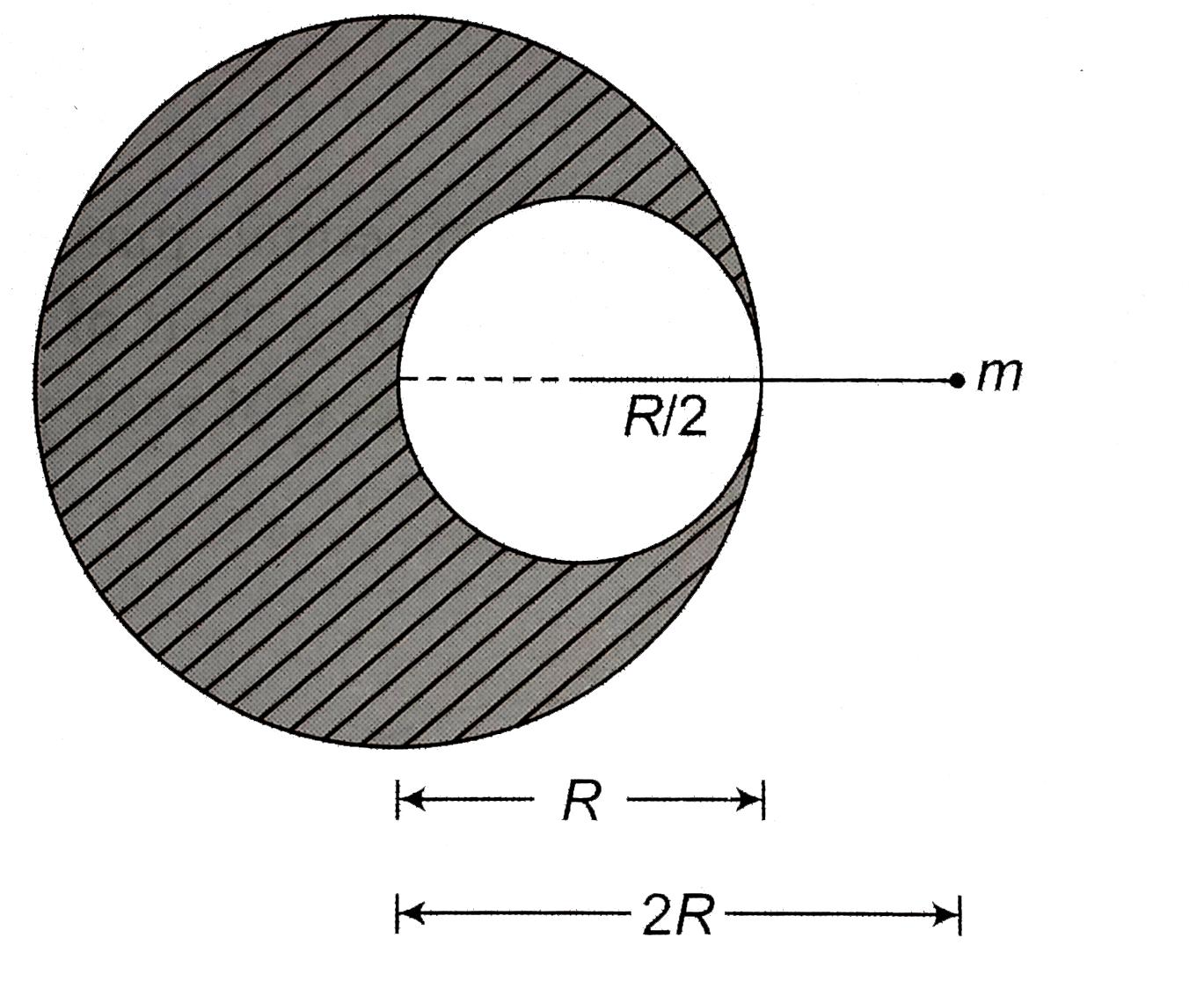
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
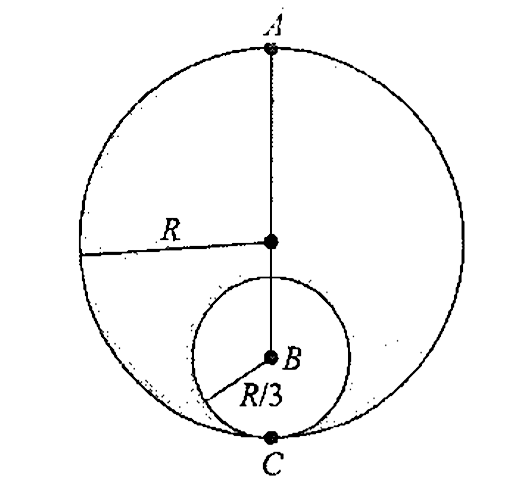 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyFrom a solid sphere of mass M and radius R, a spherical portion of radius R2 is removed. The diameter of the cavity so formed coincides with a radius of the sphere. v0 was the escape speed of a particle projected from the surface of this sphere without cavity. Then the velocity v' that must be given to a particle along O Aso that it can just reach A, starting from within the cavity, is:
AV0Bv02Cv0√2Dv04
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
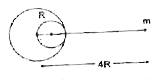
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
View SolutionA spherical hole of radius R/2 is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

View Solution
