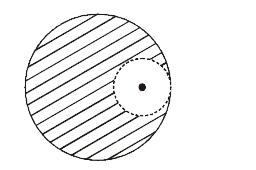
A spherical hole of radius $R / 2$ is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

A

$\frac{G M}{R^{2}}$

B

$\frac{G M}{2 R^{2}}$

C

$\frac{G M}{8 k^{2}}$

D

$\frac{7 G M}{8 R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$m' = \frac{m}{\frac{4 π R^{3}}{3}} \times \frac{4 π}{3} \frac{R^{3}}{8} = \frac{m}{8}$
$g = \frac{G m}{R^{2}} - \frac{G m^{4}}{8 R^{2}} = \frac{G m}{2 π R^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the above question, if the soild sphere is a large rock, what is the gravitational acceleration at a point on the surface of the rock at a point just above the cavity ?
A $\frac{G M}{R^{2}}$
B $\frac{G M}{2 R^{2}}$
C $\frac{G M}{8 R^{2}}$
D $\frac{7 G M}{8 R^{2}}$
Question 2 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

Ag sin $θ$
Bg sin $θ$ + a cos $θ$
Cg sin $θ$ - a cos $θ$
Da cos $θ$
Question 3 - Select One
If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
A $\frac{R^{2}}{M}$
B $\frac{M}{R^{2}}$
C $M R^{2}$
D $\frac{M}{R}$

BANSAL-MASTER PRACTICE PROBLEM-Additional topic

Home
Ask Doubt
Profile