From a thin uniform disc of radius 2R. Another disc of diameter 2R is removed. The mass of the remaining portion is m. Find the M.I. of the shaded portion about an axis passing through O and pependicular to the plane.

Mass of disc ∝ area
mA∝π(2R)2⇒mA=4M
mB∝πR2⇒mB=M
(IA)0=12×4M(2R)2=8MR2
(IB)0=(12×MR2+MR2)=3MR22
M.I. of the shaded portion I0=(IA)0−(IB)0=13MR22
4M−M=m⇒M=m3
I0=13MR22=13mR26
Topper's Solved these Questions
Similar Questions
From a circular disc of radius R, another disc of diameter R is removed. Locate c.m. of the remaining portion.
 View Solution
View SolutionFrom a disc of radius r1, a concentric disc of radius r2 is removed . The mass of the remaining portion is m. Find the M.I. of the remaining about an axis passing through the center of mass and perpendicular to the plane.
View Solution
Knowledge Check
- Question 1 - Select One
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is
 A56MR2B53MR2C512MR2D524MR2
A56MR2B53MR2C512MR2D524MR2 - Question 2 - Select One
A square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :
 A964Ma2B316Ma2C512Ma2DMa26
A964Ma2B316Ma2C512Ma2DMa26 - Question 3 - Select One
The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 mB2 cmC1 mD0.2 m
From a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionFrom a semicircular disc of radius r1, another semicircular disc of radius r2 is removed. Find the c.m. of the remaining position.
 View Solution
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
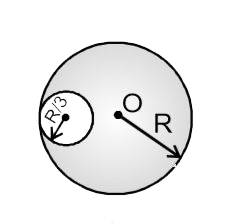 View Solution
View SolutionThe diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
View Solution

