From amongst the following curves, which one shows the variation of the velocity v with time t for a small sized spherical body falling vertically in a long column of a viscous liquid

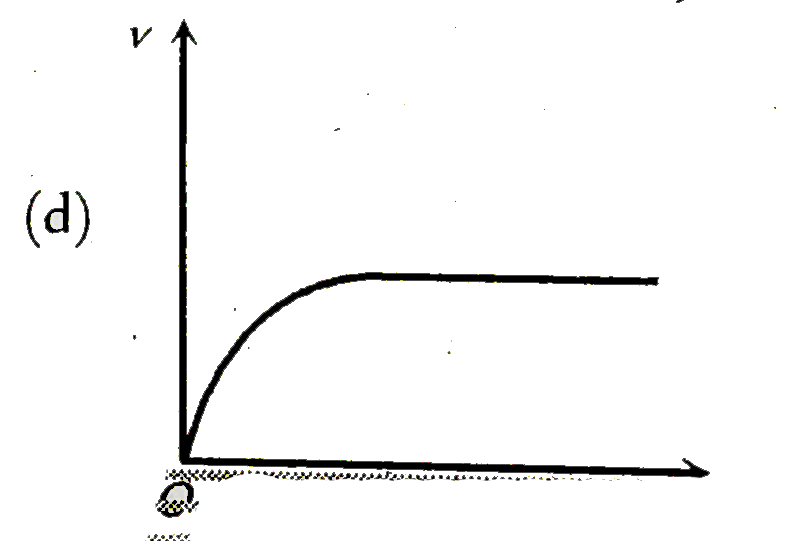
The correct Answer is:D
To determine the variation of velocity v with time t for a small spherical body falling vertically in a long column of viscous liquid, we can analyze the motion based on the principles of fluid mechanics, particularly Stokes' law.
1. Understanding the Forces Acting on the Sphere:
- When a small spherical body falls through a viscous fluid, it experiences three main forces:
- Weight (W): The gravitational force acting downwards, given by W=mg, where m is the mass of the sphere and g is the acceleration due to gravity.
- Buoyant Force (B): The upward force exerted by the fluid, given by Archimedes' principle. For a sphere of volume V, B=ρfVg, where ρf is the density of the fluid.
- Drag Force (F_d): The resistance force exerted by the fluid, which according to Stokes' law is given by Fd=6πηrv, where η is the viscosity of the fluid, r is the radius of the sphere, and v is the velocity of the sphere.
2. Setting Up the Equation of Motion:
- As the sphere falls, it accelerates until the drag force equals the net downward force (weight minus buoyant force). At this point, the sphere reaches its terminal velocity vt.
- The equation can be set up as follows:
mg−ρfVg−6πηrv=0
- Rearranging gives:
mg−ρfVg=6πηrv
3. Identifying Terminal Velocity:
- The terminal velocity vt is reached when the net force acting on the sphere becomes zero. Thus, we can express terminal velocity as:
vt=(mg−ρfVg)6πηr
- This indicates that the terminal velocity is constant and does not change with time once reached.
4. Graphical Representation:
- Initially, as the sphere starts falling, its velocity increases due to the net force acting on it. However, as it accelerates, the drag force increases until it balances the weight of the sphere, leading to a constant velocity.
- Therefore, the graph of velocity v versus time t will show an initial increase in velocity, which will then level off to a constant value (the terminal velocity).
5. Conclusion:
- The correct curve that represents this scenario will start at zero, rise steeply at first, and then flatten out as it approaches the terminal velocity. This indicates that the velocity increases with time until it reaches a constant value.
- When a small spherical body falls through a viscous fluid, it experiences three main forces:
- Weight (W): The gravitational force acting downwards, given by W=mg, where m is the mass of the sphere and g is the acceleration due to gravity.
- Buoyant Force (B): The upward force exerted by the fluid, given by Archimedes' principle. For a sphere of volume V, B=ρfVg, where ρf is the density of the fluid.
- Drag Force (F_d): The resistance force exerted by the fluid, which according to Stokes' law is given by Fd=6πηrv, where η is the viscosity of the fluid, r is the radius of the sphere, and v is the velocity of the sphere.
- As the sphere falls, it accelerates until the drag force equals the net downward force (weight minus buoyant force). At this point, the sphere reaches its terminal velocity vt.
- The equation can be set up as follows:
mg−ρfVg−6πηrv=0
- Rearranging gives:
mg−ρfVg=6πηrv
- The terminal velocity vt is reached when the net force acting on the sphere becomes zero. Thus, we can express terminal velocity as:
vt=(mg−ρfVg)6πηr
- This indicates that the terminal velocity is constant and does not change with time once reached.
- Initially, as the sphere starts falling, its velocity increases due to the net force acting on it. However, as it accelerates, the drag force increases until it balances the weight of the sphere, leading to a constant velocity.
- Therefore, the graph of velocity v versus time t will show an initial increase in velocity, which will then level off to a constant value (the terminal velocity).
- The correct curve that represents this scenario will start at zero, rise steeply at first, and then flatten out as it approaches the terminal velocity. This indicates that the velocity increases with time until it reaches a constant value.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Asseration and Reason
28 Videos
- FLUID MECHANICSBOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Fluid Mechanics
19 Videos
- FLUID MECHANICSBOOK - ERRORLESS CHAPTER - FLUID MECHANICSEXERCISE - Critical Thinking
14 Videos
- ELASTICITYBOOK - ERRORLESS CHAPTER - ELASTICITYEXERCISE - Self Evaluation Test
11 Videos
- FRICTIONBOOK - ERRORLESS CHAPTER - FRICTIONEXERCISE - MCQ S
125 Videos
Similar Questions
Knowledge Check
From amongst the following curves, which one shows the variation of the velocity v with t for a small sized spherical body falling vertically in long column of viscous liquid
A B
B C
C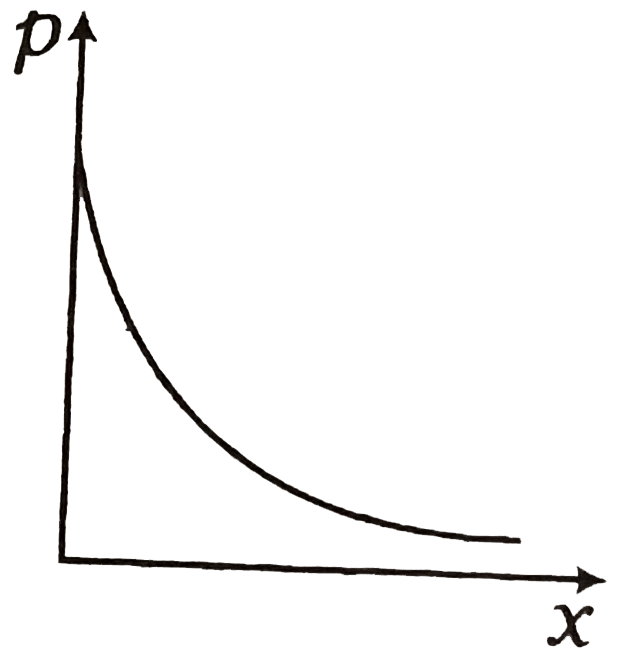 D
D
Which one of the following curves shows correxctly the variation of velocity v with time t for a small spherical body fallig vertically in a long column of viscous liquid ?
A B
B C
C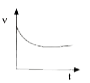 D
D
The terminal velocity of a small sized speherical body of radius r falling in a viscous liquid is proportional to :
A1r2B1rCrDr2
A body is thrown vertically upwards which graph represents variation of velocity w.r.t time
View SolutionWhich of the following shows velocity (v) - time (t) graph for falling apple?
View SolutionWhich one of the following graphs shows the variation of magnetic induction B which distance r from a long wire carrying a current ?
View SolutionWhich of the following optiona correctly describes the variation of the speed υ and acceleration a of a point mass falling vertically in a viscous medium that applies a force F=-KC where K is a constant on the body ? (graphs are schematic and not drawn to scale)
View SolutionWhich of the following option correctly describes the variation of the speed and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force F=−kv, where 'k' is constant, on the body?
(Graphs are schematic and drawn to scale)
View Solution
