Which of the following option correctly describes the variation of the speed and acceleration 'a' of a point mass falling vertically in a viscous medium that applies a force F=−kv, where 'k' is constant, on the body?
(Graphs are schematic and drawn to scale)
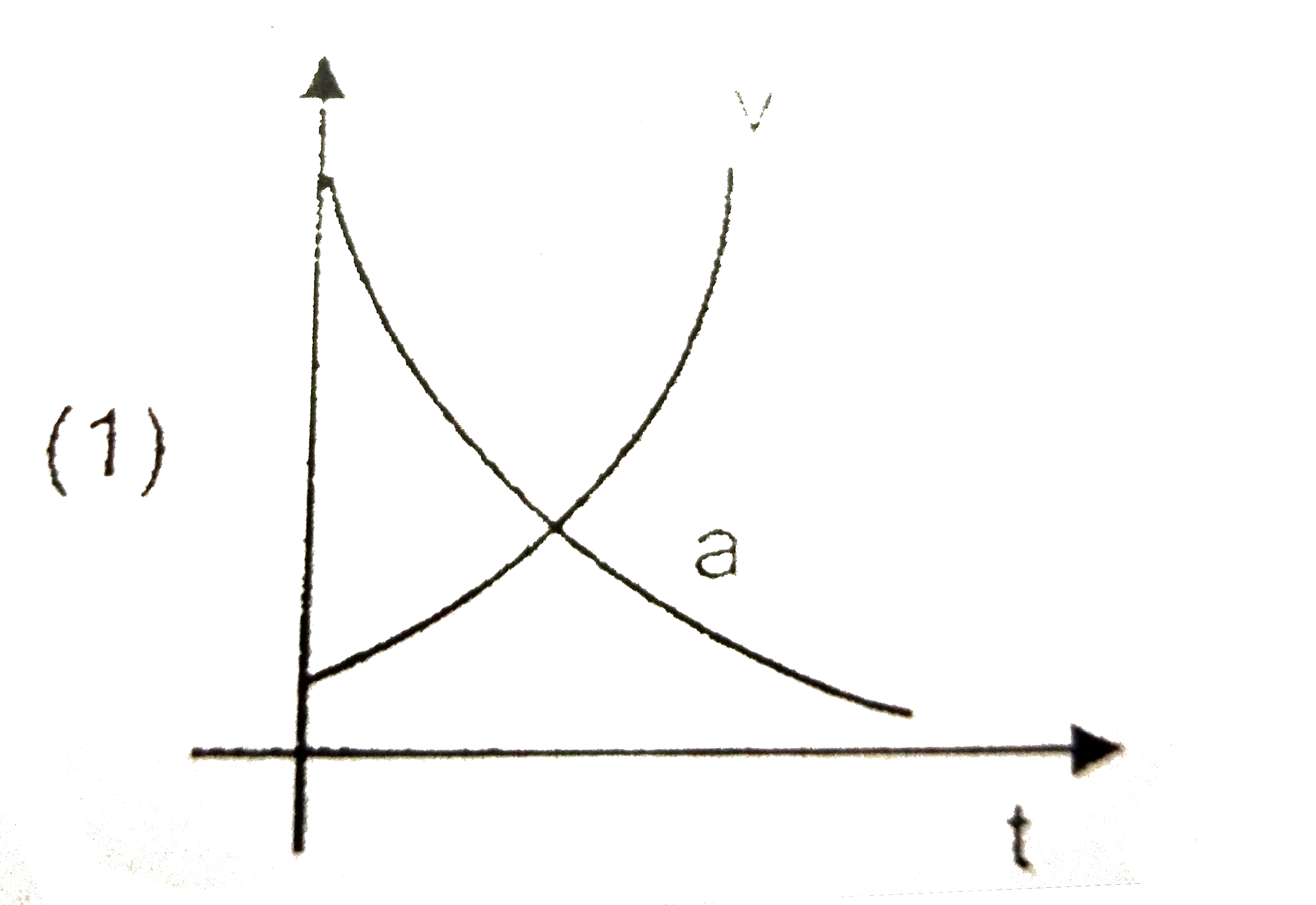
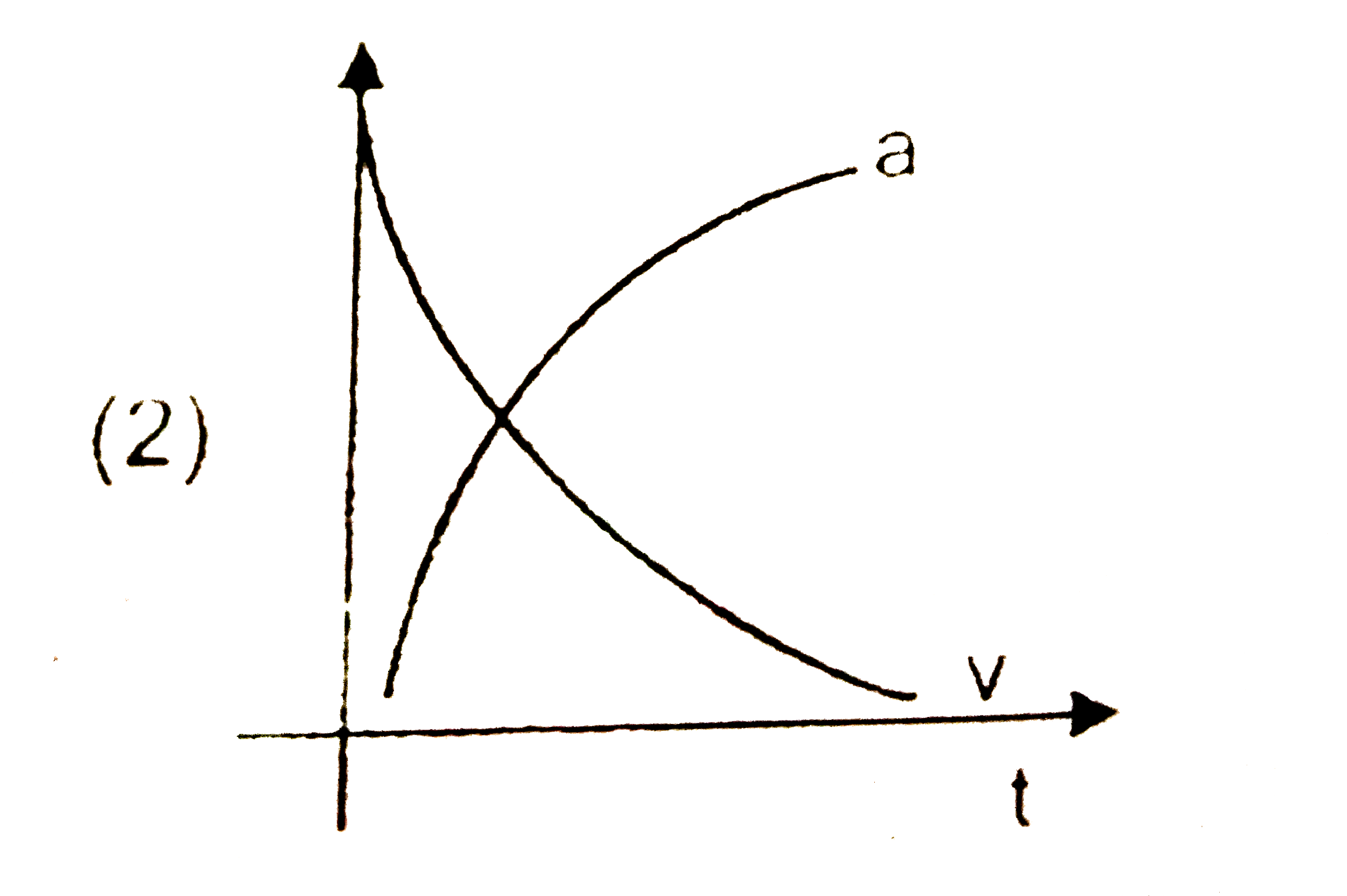
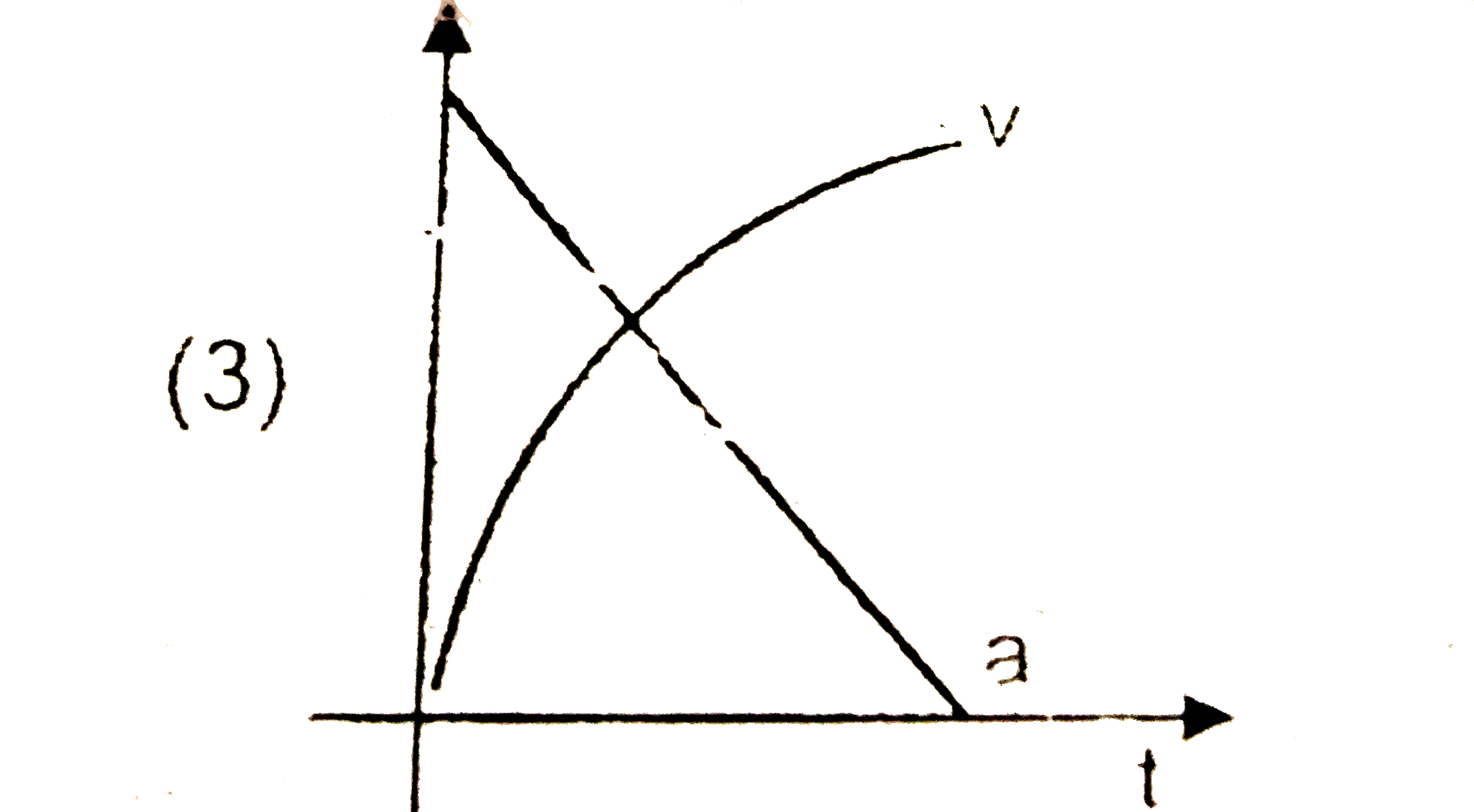
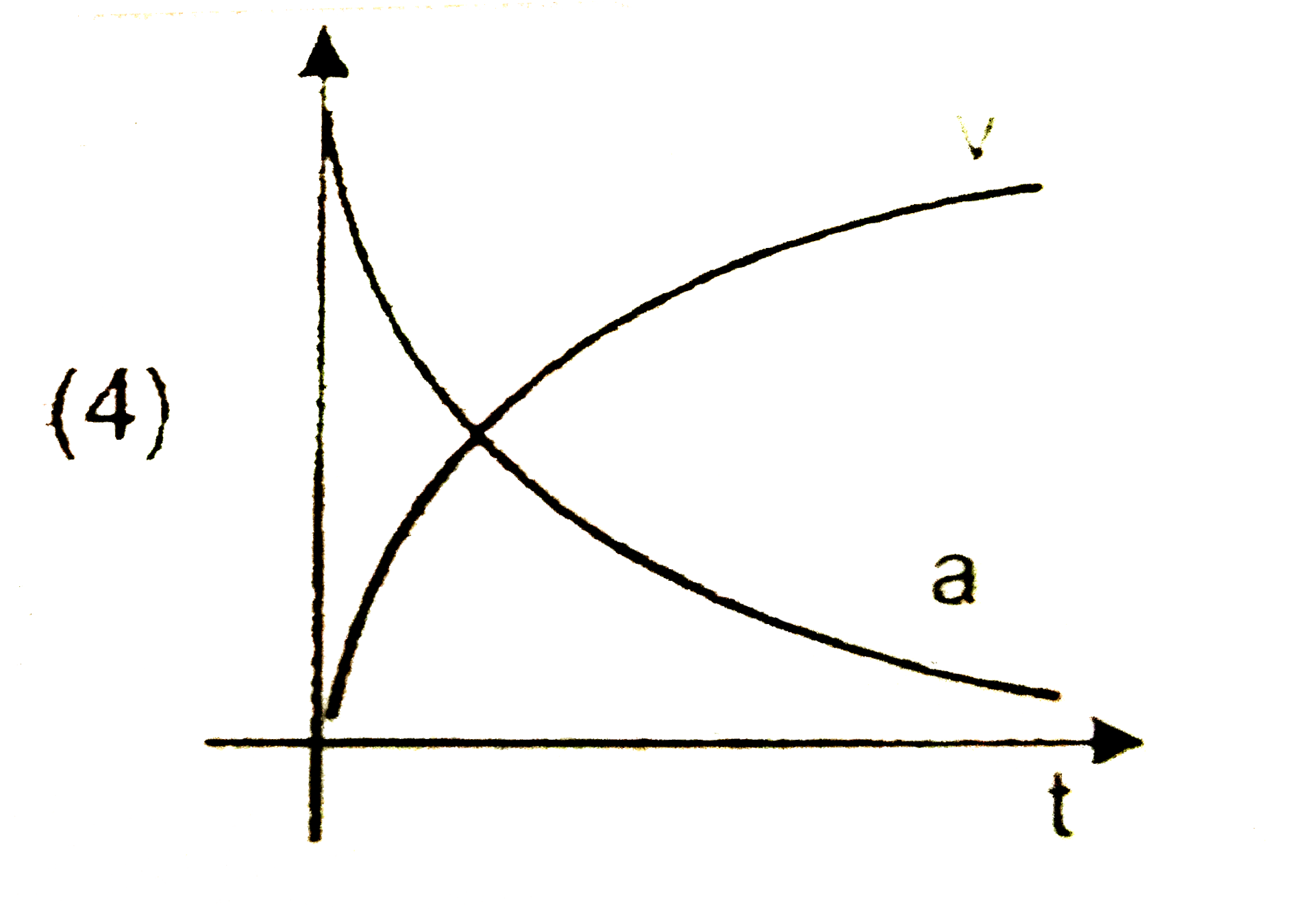
The correct Answer is:D
To solve the problem of determining the variation of speed v and acceleration a of a point mass falling vertically in a viscous medium, we can follow these steps:
Step 1: Understand the Forces Acting on the Mass
The forces acting on the mass are:
- The gravitational force Fg=mg acting downwards.
- The viscous drag force Fd=−kv acting upwards.
Step 2: Write the Equation of Motion
Using Newton's second law, we can set up the equation of motion:
ma=mg−kv
Rearranging gives:
ma=mg−kv⟹a=g−kmv
Step 3: Identify Terminal Velocity
At terminal velocity vt, the acceleration a becomes zero:
0=g−kmvt⟹vt=mgk
Step 4: Express Acceleration in Terms of Velocity
From the equation a=g−kmv, we can see that as v approaches vt, the acceleration a approaches zero.
Step 5: Analyze the Behavior of Velocity Over Time
To find how velocity changes with time, we can rearrange the equation:
dvdt=g−kmv
This is a first-order linear differential equation. Solving this will show that velocity increases towards vt exponentially.
Step 6: Solve the Differential Equation
Separating variables and integrating:
∫1g−kmvdv=∫dt
This leads to:
t=−mkln⎛⎝g−kmvg⎞⎠
From this, we can derive that:
v(t)=vt(1−e−kmt)
This shows that velocity increases exponentially and approaches vt.
Step 7: Determine the Behavior of Acceleration
Since a=g−kmv and v increases over time, a decreases over time and approaches zero as v approaches vt.
Final Conclusion
- The velocity v increases exponentially and approaches vt.
- The acceleration a decreases exponentially and approaches zero.
The forces acting on the mass are:
- The gravitational force Fg=mg acting downwards.
- The viscous drag force Fd=−kv acting upwards.
Using Newton's second law, we can set up the equation of motion:
ma=mg−kv
Rearranging gives:
ma=mg−kv⟹a=g−kmv
At terminal velocity vt, the acceleration a becomes zero:
0=g−kmvt⟹vt=mgk
From the equation a=g−kmv, we can see that as v approaches vt, the acceleration a approaches zero.
To find how velocity changes with time, we can rearrange the equation:
dvdt=g−kmv
This is a first-order linear differential equation. Solving this will show that velocity increases towards vt exponentially.
Separating variables and integrating:
∫1g−kmvdv=∫dt
This leads to:
t=−mkln⎛⎝g−kmvg⎞⎠
From this, we can derive that:
v(t)=vt(1−e−kmt)
This shows that velocity increases exponentially and approaches vt.
Since a=g−kmv and v increases over time, a decreases over time and approaches zero as v approaches vt.
- The velocity v increases exponentially and approaches vt.
- The acceleration a decreases exponentially and approaches zero.
Similar Questions
Which one of the following given graphs represents the variation of rate constant (k) with temperature (f) for an endothermic reaction ?
View SolutionIn a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schematic and not drawn to scale]
View Solution
Knowledge Check
- Question 1 - Select One
Which of the following optiona correctly describes the variation of the speed υ and acceleration a of a point mass falling vertically in a viscous medium that applies a force F=-KC where K is a constant on the body ? (graphs are schematic and not drawn to scale)
A_E01_264_O01.png) B
B_E01_264_O02.png) C
C_E01_264_O03.png) D
D_E01_264_O04.png)
- Question 2 - Select One
From amongst the following curves, which one shows the variation of the velocity v with t for a small sized spherical body falling vertically in long column of viscous liquid
A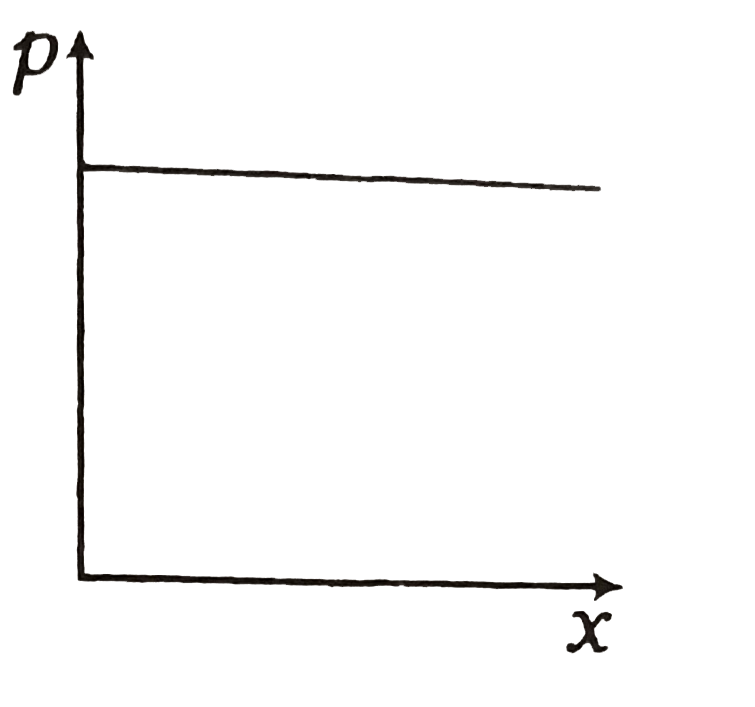 B
B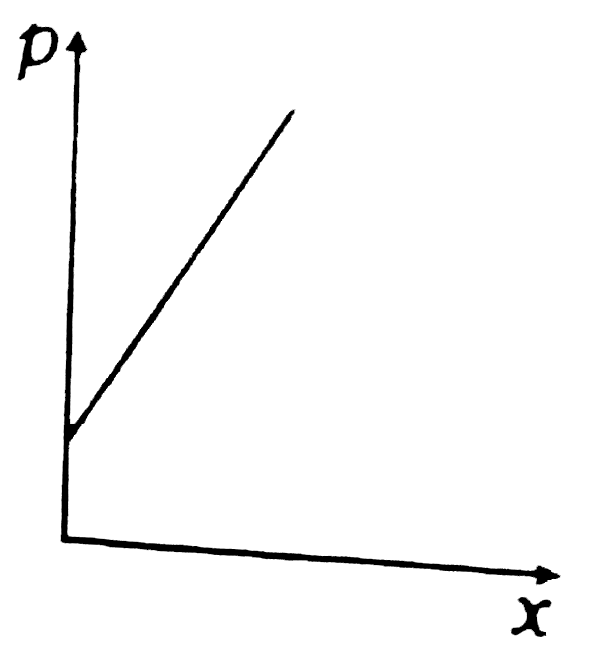 C
C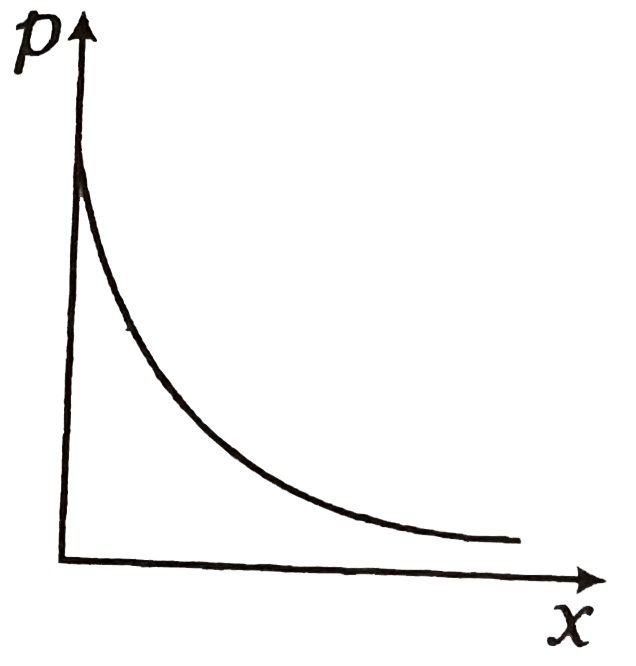 D
D
- Question 3 - Select One
Which of the following graphs correctly shows variation between the restoring force I F I and distance from the mean position (x) of a particle performing linear S.H.M.?
A B
B C
C D
D
From amongst the following curves, which one shows the variation of the velocity v with time t for a small sized spherical body falling vertically in a long column of a viscous liquid
View SolutionAn oil drop of mass m and falls through a medium that offers a viscous drag force. F. if the velocity of the drop is constant it means that
View SolutionIn a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schematic and not drawn to scale]
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionFor a simple pendulum, a graph is plotted between itskinetic energy (KE) and potential energy (PE)against its displacement d. Which one of the following represents these correctly? (graph are schematic and not drawn to scale)
View Solution

