Given n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
To solve the problem, we need to determine how to combine n resistors, each with resistance R, to achieve both the maximum and minimum effective resistance. We will also find the ratio of the maximum to minimum resistance.
1. Maximum Effective Resistance:
- To achieve the maximum effective resistance, we should connect all n resistors in series.
- The formula for the total resistance Rmax in series is:
Rmax=R+R+R+…+R(n times)=nR
- Therefore, the maximum effective resistance when n resistors are connected in series is:
Rmax=nR
2. Minimum Effective Resistance:
- To achieve the minimum effective resistance, we should connect all n resistors in parallel.
- The formula for the total resistance Rmin in parallel is given by:
1Rmin=1R+1R+…+1R(n times)=nR
- Inverting this gives us the effective resistance:
Rmin=Rn
3. Ratio of Maximum to Minimum Resistance:
- Now, we can find the ratio of the maximum effective resistance to the minimum effective resistance:
Ratio=RmaxRmin=nRRn=nR⋅nR=n2
- Thus, the ratio of the maximum resistance to the minimum resistance is:
Ratio=n2:1
Final Answer:
- Maximum effective resistance: nR
- Minimum effective resistance: Rn
- Ratio of maximum to minimum resistance: n2:1
- To achieve the maximum effective resistance, we should connect all n resistors in series.
- The formula for the total resistance Rmax in series is:
Rmax=R+R+R+…+R(n times)=nR
- Therefore, the maximum effective resistance when n resistors are connected in series is:
Rmax=nR
- To achieve the minimum effective resistance, we should connect all n resistors in parallel.
- The formula for the total resistance Rmin in parallel is given by:
1Rmin=1R+1R+…+1R(n times)=nR
- Inverting this gives us the effective resistance:
Rmin=Rn
- Now, we can find the ratio of the maximum effective resistance to the minimum effective resistance:
Ratio=RmaxRmin=nRRn=nR⋅nR=n2
- Thus, the ratio of the maximum resistance to the minimum resistance is:
Ratio=n2:1
- Maximum effective resistance: nR
- Minimum effective resistance: Rn
- Ratio of maximum to minimum resistance: n2:1
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive
18 Videos
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
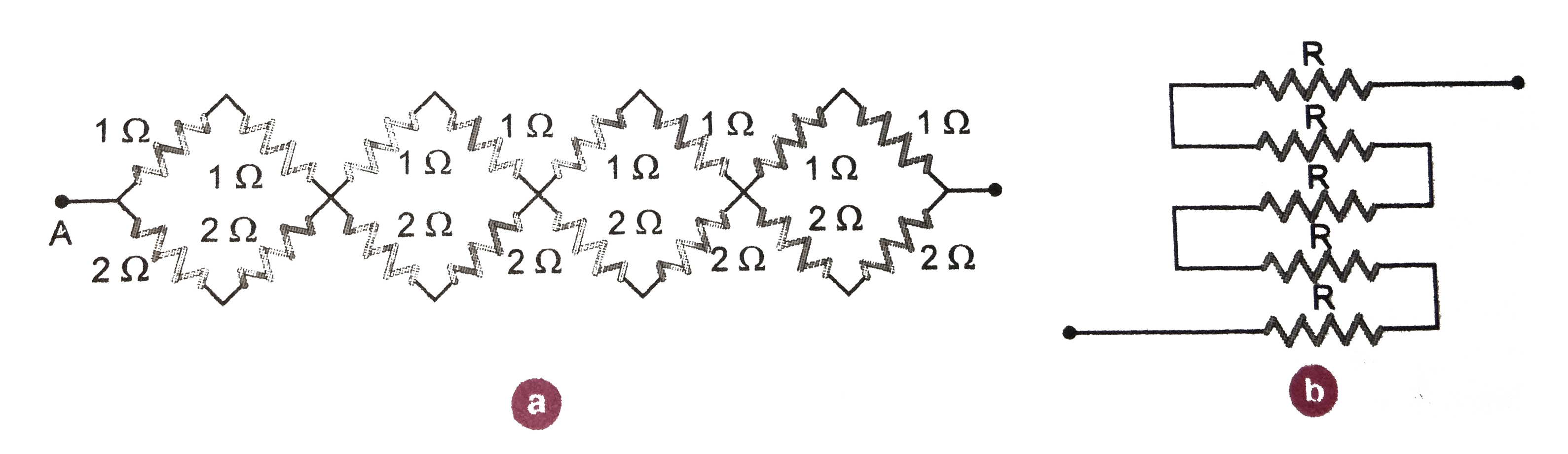
View Solution
Knowledge Check
n resistors each of resistance R first combine to give maximum effective resistgance and then combine to give minimum. The ratio of the maximum resistance is
AnBn2Cn2−1Dn3We have n resistors each of resistance R. The ratio of the combination for maximum and minimum values is
AnBn2Cn3D1n
Given n resistors each of resistance R, how will you combine them to get the (i) maximum, and (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
View SolutionIf n resistors each of resistance r are connected to get (i) maximum possible resistance (ii) minimum possible resistance. Compute the ratio between values of resistances obtained in (i) and (ii).
View SolutionYou are given n resistors each of resistance r .These are first connected to get minimum resistance .In the secoind case these are again connected differently to get maximum possible resistance. Compute the ratio between the minimum and maximum value of resistance so obtained.
View Solutionn equal resistors are first connected in series and then connected in parallel. What is the ratio of the maximum to the minimum resistance ?
View SolutionGiven three resistors of resistances 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of 115Ω ?
View SolutionYou are given 10 resistors each of resistance 2Ω. First they are connected to obtain possible minimum resistance. Then they are connected to obtain possible maximum resistance. The ratio of maximum and minimum resistance is ________________ .
View Solution
